Activity waves and freestanding vortices in subcritical active matter

In a recent paper published in PNAS, Hugues Chaté (IRAMIS/SPEC), Xia-qing Shi and the group of Tian Hui Zhang (Soochow University) show that subcritical active matter exhibits novel collective self-organized dynamics. They used “Quincke rollers”, i.e. colloidal spheres at the bottom of a cell filled with conducting fluid submitted to a vertical electric field. Working just below the field strength triggering the rotation of an isolated particle allows the emergence of such spectacular phenomena as arbitrarily large self-standing vortices made of thousands of particles.

Virtually all of the many active matter systems studied so far are made of units (biofilaments, cells, colloidal particles, robots, animals, etc.) that move even when they are alone or isolated. Their collective properties continue to fascinate and we now understand better how they are unique to the bulk transduction of energy into work.

A recent work just published in PNAS demonstrates that systems in which isolated but potentially active particles do not move can exhibit specific and remarkable collective properties. Combining experiments, theory, and numerical simulations, this paper shows that such subcritical active matter can be realized with Quincke rollers.

Since the early work of Quincke at the end of the 19^th century, it is well known that dielectric colloidal particles immersed in a conducting fluid subjected to a vertical DC electric field undergo an instability leading to their rotation in the fluid when the field strength E is large enough. When the particles are denser than the fluid, they rest on the bottom surface, and start rolling in an arbitrary horizontal direction beyond the instability onset E_c.

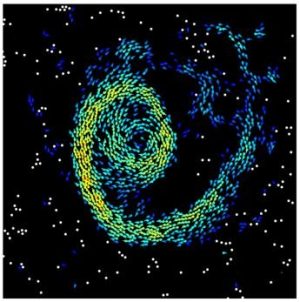
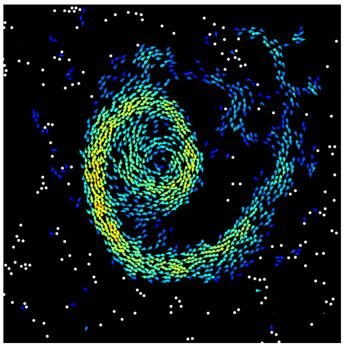
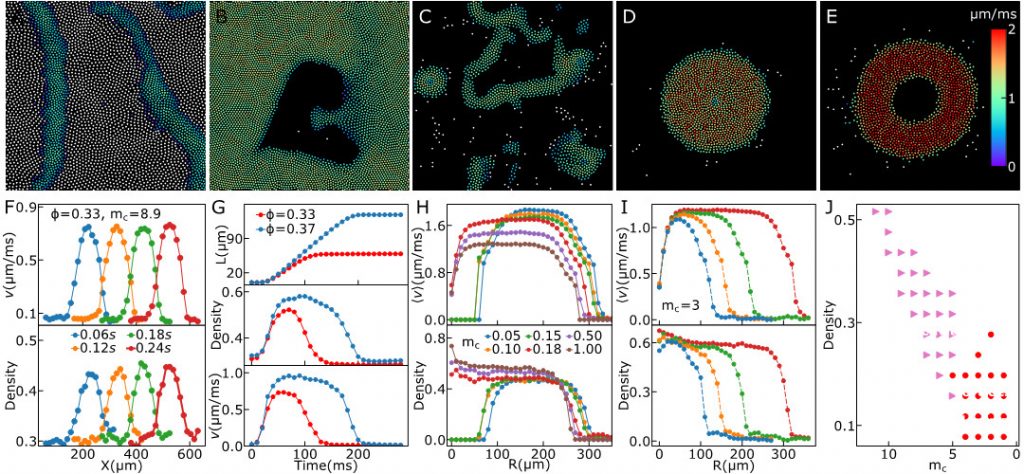
The collective dynamics of Quincke rollers have been studied in the supercritical regime E>E_c,. The recent PNAS publication shows that spectacular collective phenomena emerge also when working below E_c, essentially because particles near each other can start rolling even for E< E_c.The phenomena reported include fast activity waves reminiscent of excitable systems, and stable arbitrarily large self-standing vortices made of thousands of particles moving at the same speed.

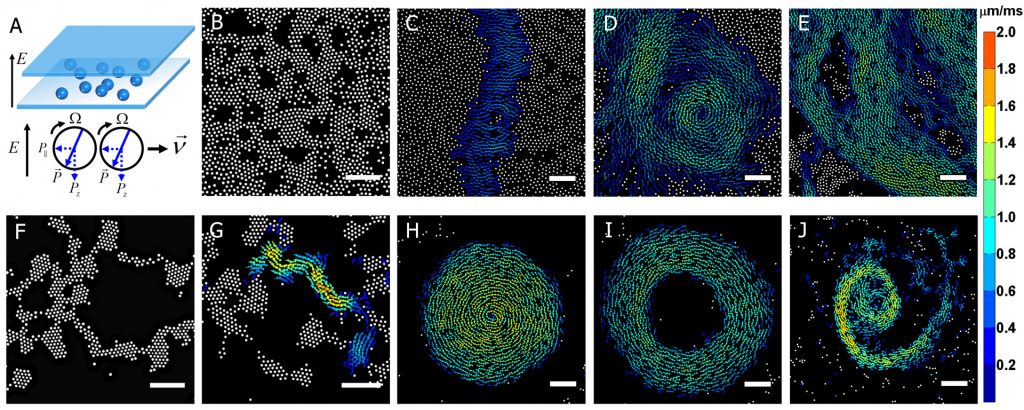
Experimental results. (A) Schematics of the experimental setup. (B-J) Various snapshots with superimposed velocities. Space bar = 100 μm. Colors indicate speed, quiescent particles are left white. Top and bottom row respectively show high and low area fraction cases ((B-E) Φ ≃ 0.4; (F-J) Φ ≃ 0.2) arranged by increasing values of E/Ec from left to right. (B,F) quiescent clusters with local hexatic order obtained at E = 0.65 Ec. (C) wide activity wave at E = 0.89 Ec. (D) large scale subcritical flock at E = 0.98 Ec. (E) subcritical flocking at E = 0.98 Ec. (G) localized activity at E = 0.9 Ec. (H) freestanding vortex at E = 0.948 Ec. (I) freestanding donut at E = 0.968 Ec. (J) spiral flock at E = 0.98 Ec.

These remarkable collective dynamics cannot be accounted for by models usually invoked to be valid for such systems. A new type of mathematical model, motivated by experimental results, is introduced and shown to account for all observed phenomena.

Modeling results. (A-E) Typical configurations in a domain of linear size 960 μm with periodic boundary conditions. Disks of diameter 10 μm are centered on particle’s positions. Immobile particles are in white while moving ones are colored by their speed (colormap in (E)). (A) activity waves propagating from left to right in a dense system (mc = 8.9, Φ = 0.33, about 3900 particles). (B) subcritical flocking regime in a dense system with particles mostly moving from right to left (mc = 3, Φ = 0.47, about 5530 particles). (C-E) vortex and donut formation (Φ = 0.12, 1433 particles). (C) snapshot during transient (mc = 3). (D) final vortex comprising most particles in the system (mc = 0.5). (E) final donut configuration comprising most particles in the system (mc = 0.05).

Reference:

« Activity waves and freestanding vortices in populations of subcritical Quincke rollers” ,
Zeng Tao Liu, Yan Shi, Yongfeng Zhao, Hugues Chaté, Xia-qing Shi, and Tian Hui Zhang, PNAS 118 (40) e2104724118 (2021)

Contact CEA-IRAMIS : Hugues Chaté (SPEC/SPHYNX)

Collaboration:

Z.T. Liu, Y. Shi, Y. Zhao, H. Chaté, X.-q. Shi, and T.H. Zhang, Center for Soft Condensed Matter Physics and Interdisciplinary Research, Soochow University, Suzhou 215006, China.