La plupart des fluides qui nous entourent -atmosphère, océans, rivières- sont turbulents et caractérisés par des mouvements tourbillonnaires et fluctuants sur une large gamme d’échelles spatiale et temporelle. Ainsi, alors qu’on connaît leurs équations d’évolution – les équations de Navier-Stokes – depuis près de 200 ans, on ne peut que rarement reproduire leur comportement « in silico » avec une simulation numérique sans modèle additionnel pour les petites échelles, faute d’espace mémoire et de capacité de calcul suffisants, même sur les ordinateurs actuels les plus performants.
Ainsi, pour comprendre les propriétés des écoulements très turbulents, les expériences « in fluido » restent incontournables, même s'il est souvent difficile d’avoir accès à des cartographies détaillées du mouvement tourbillonnaire à toutes les échelles, faute de moyens de mesures adaptés.
Une collaboration entre les équipes expérimentales du SPEC/SPHYNX et du LMFL et une équipe numérique du LIMSI a réussi pour la première fois la prouesse de produire une comparaison détaillée des propriétés locales et globales de la turbulence sur une grande gamme d’échelles dans un écoulement de von Kármán. Cette avancée a pu être obtenue grâce à des méthodes innovantes de simulations numériques et des méthodes d’imagerie laser à très haute résolution. Ces études vont prochainement être complétées à des échelles encore plus petites grâce à l’arrivée au SPEC/SPHYNX d'u' nouveau dispositif « Giant Von Kármán ».

La plupart des fluides qui nous entourent – atmosphère, océans, rivières – sont turbulents et caractérisés par des mouvements tourbillonnaires et fluctuants sur une gamme d’échelles très grande. Cela rend leur évolution chaotique et impacte nos possibilités de prévoir la météorologie, le climat ou la pénétration des objets dans l’air (avions, automobiles…). Les équations de Navier-Stokes qui gouvernent les fluides sont pourtant connues depuis près de deux cents ans. Cependant, leur application aux écoulements réalistes est limitée par deux facteurs :
- d’une part on ignore si ces équations sont mathématiquement bien posées et pourraient développer des singularités qui briseraient l’unicité des solutions ;
- ensuite leur résolution par des simulations numériques directes se heurte au mur du nombre de degrés de libertés : ce dernier peut atteindre 1023 pour un écoulement atmosphérique, ce qui n’est pas traitable par les ordinateurs actuels, ni en terme de taille mémoire, ni en terme de temps de calculs.
L’idée est alors venue de remplacer les équations de Navier-Stokes par des modèles plus légers, accessibles aux simulations numériques, tout en conservant les propriétés macroscopiques de l’écoulement. C’est ce qui est utilisé de façon courante dans l’industrie, la météorologie et le climat. Il est néanmoins ardu d’obtenir un modèle qui reproduise avec fidélité la richesse de l’écoulement réel. De plus, tout modèle comporte des paramètres ajustables qui nécessitent une calibration pour garantir que le modèle reproduira fidèlement le comportement d’un écoulement turbulent. Les résultats issus de ces simulations doivent alors être confrontés à ceux provenant d’expériences de laboratoire.
Jusque récemment, ces comparaisons étaient limitées par l’impossibilité de cartographier précisément un écoulement turbulent en laboratoire. Mais depuis l’avènement de l’imagerie par tomographie laser, on sait aujourd'hui mesurer les trois composantes de la vitesse d’un écoulement en volume, avec une résolution millimétrique et à des cadences de 1 kHz. Ces progrès ont pu être utilisés pour comparer de façon quantitative et pour une même géométrie, un écoulement très turbulent en laboratoire, avec des données issues de simulations numériques : soit directement de l’équation de Navier-Stokes (DNS – Direct Numerical Simulations), soit d’équations LES (Large Eddy Simulation) incluant un modèle aux petites échelles, et permettant de simuler un écoulement dans des conditions beaucoup plus turbulentes.
Ce travail, mené conjointement avec des équipes du LMFL, du LIMSI et de deux universités au Texas, permet d’une part de garantir la qualité remarquable des mesures expérimentales réalisées grâce aux comparaisons avec les DNS, d’autre part de confirmer le modèle LES en opérant dans des conditions plus turbulentes et inaccessibles encore actuellement aux DNS.
La géométrie utilisée est celle de l’écoulement de von Kármán. Ce dispositif génère par l’entraînement de deux turbines contrarotatives un écoulement fortement turbulent dans un cylindre. Cette géométrie assez compacte permet d’atteindre des taux de turbulence comparables à ceux observés dans l’atmosphère ou l’océan. Malgré sa simplicité, ce dispositif est très difficile à simuler numériquement, puisqu’il faut rendre compte du mouvement des turbines. Cet écueil a été surmonté grâce à l’introduction de méthodes de pénalisation innovantes (optimisation en tenant compte des contraintes), couplées à un maillage très résolu près des turbines.
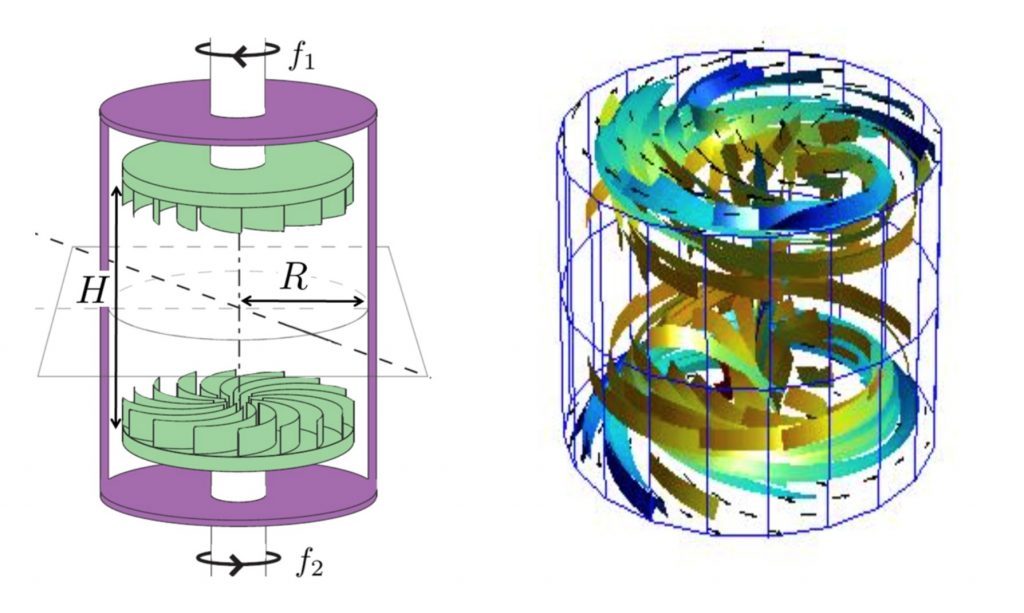
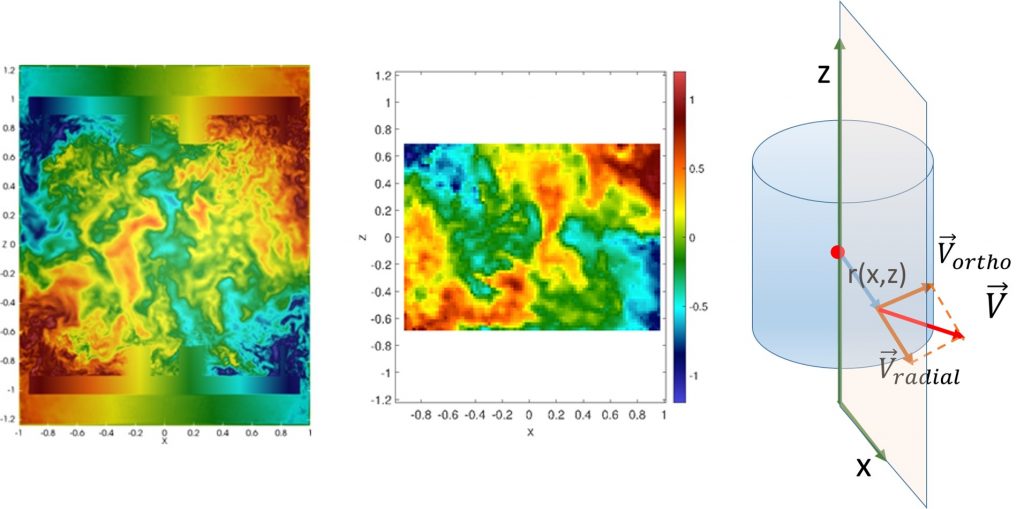
Du point de vue expérimental, les champs de vitesses sont mesurés par le suivi de petites particules de verre préalablement mélangées au fluide (ensemencement). Un montage optique minutieux permet de filmer avec des caméras les particules éclairées par un laser et ainsi obtenir le champ de vitesse dans la zone de mesure. La figure 1 montre un exemple de comparaison de la composante orthoradiale du champ de vitesse mesurée « in silico » et « in fluido ». La comparaison est excellente, tant du point de vue de la structure de l’écoulement qu’au niveau de l’intensité des fluctuations.
D’autres comparaisons ont été également couronnées de succès, concernant notamment la dissipation de l'énergie [1] et sa répartition à travers les échelles [2]. Finalement, la comparaison a également permis de valider provisoirement un nouveau modèle LES, qui prend en compte la nature singulière des mouvements à petite échelle.
Pour progresser dans la compréhension de la nature et de la dynamique de ces petites échelles potentiellement singulières, nous avons initié une nouvelle collaboration avec le LMFL à Lille, et mis au point dans le cadre de l’ANR EXPLOIT et du projet CEA VORTEX un nouveau dispositif expérimental, permettant un gain de résolution spatiale d’un facteur 5. Ce dispositif appelé « GVK – Giant Von Karman » est maintenant installé dans un bâtiment du SPEC. Les premières expériences de qualification de l'instrument sont en cours, pour, sans attendre la fin de l'épidémie de COVID19, nous livrer une part de ses premiers secrets.
Références :
[1] Turbulence in realistic geometries with moving boundaries: When simulations meet experiments, Computers & Fluids, 214 (2021) 104750.
[2] On the nature of intermittency in a turbulent von Kármán flow
H. Faller, D. Geneste, T. Chaabo, A. Cheminet, V. Valori, Y. Ostovan, L. Cappanera, Ch. Cuvier, F. Daviaud, J.-M. Foucaut, J.-L. Guermond, J.-Ph. Laval, C. Nore, V. Padilla, C. Wiertel and B. Dubrulle, Journal of Fluid Mechanics, 914 (2021) A2.
Three-dimensional analysis of precursors to non-viscous dissipation in an experimental turbulent flow
P. Debue, V. Valori, C. Cuvier, F. Daviaud, J.M. Foucaut, J. Laval, C. Wiertel, V. Padilla and B. Dubrulle, Journal of Fluid Mechanics, 914 (2021) A9.
Contact CEA-IRAMIS : Bérengère Dubrulle (SPEC/SPHYNX)
Collaboration :
- A. Cheminet, F. Daviaud , P. Debue, B. Dubrulle, H. Faller, D. Geneste, D. Kuzzay, V. Padilla, E-W. Saw, V. Valori, C. Wiertel-Gasquet, SPEC/SPHYNX
- C. Nore LIMSI – Laboratoire d'Informatique pour la Mécanique et les Sciences de l'Ingénieur, Orsay, France
- J-L Guermond, Department of mathematics, Texas A&M University et L. Cappanera, Department of Mathematics, University of Houston,
- T. Chaabo, C. Cuvier, J-M Foucaut, J-P. Laval, Y. Ostovan : LMFL – Laboratoire de Mécanique des Fluides de Lille, France.




