Les séismes majeurs sont imprévisibles et pourtant l'analyse statistique des évènements précurseurs et des répliques au choc principal suivent des lois statistiques aujourd'hui bien établies, mais dont l'origine reste encore très mal comprise.
En physique statistique, les mêmes lois peuvent s'appliquer à des systèmes en apparence très différents. Il suffit généralement qu'ils présentent une dimensionnalité et certaines propriétés de symétrie identiques. Il est ainsi tentant de rapprocher les études sismologiques de celles concernant la fracture des matériaux.
Des chercheurs des laboratoires de l’IRAMIS/SPEC/SPHYNX du CEA Saclay et du LTDS-Lyon, associés au CNRS, ont étudié les événements acoustiques émis lors de la propagation d’une fissure unique au sein d'un matériau hétérogène fragile, sollicité en tension. Comme cela a été observé pour un endommagement en compression, ils mettent alors en évidence que l'organisation statistique de ces évènements suit des lois d'échelles similaires à celles observées dans l'étude des séismes. Le système modèle étudié de l'avancée d'une fracture unique étant par nature plus simple et bien défini, il a été possible de comprendre dans ce cas l’origine de ces lois statistiques. Ceci ouvre de nouvelles pistes pour interpréter les lois d'échelles et leur utilisation en sismologie ou pour le suivi de l'endommagement des matériaux.
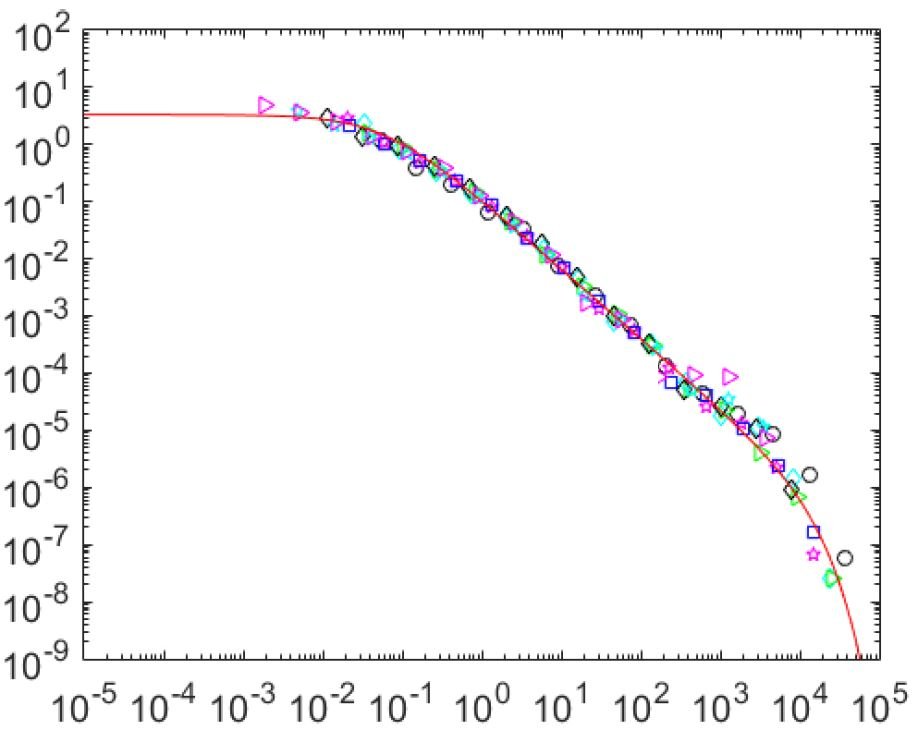
Être en mesure de prévoir la rupture d'un matériau reste un défi majeur, encore largement hors d’atteinte. Le comportement en rupture observé à l’échelle macroscopique est en effet très sensible aux inhomogénéités de structure (défauts, imperfections…) jusqu'aux plus fines échelles. Cette sensibilité aux conditions locales, se traduit par des fluctuations statistiques importantes, a priori incompatibles avec le principe de déterminisme, pierre angulaire de l’ingénierie mécanique ; tremblements de terre, éboulements de terrain, et (certains) effondrements de structures bâties illustrent de manière malheureuse nos limites actuelles !
Il n’existe à l’heure actuelle pas d’outils permettant de prédire l’occurrence des microfissures. En revanche, il a été montré par des études de l’émission acoustique induite [1] que les événements s’organisent pour former des séquences de répliques vérifiant un certain nombre de lois d’échelle initialement obtenues en sismicité :
- la loi de Gutenberg-Richter, qui donne la distribution en énergie** des évènements. Elle stipule que le nombre d’événements observés d'énergie supérieure à E décroit en loi de puissance avec E, (N ~ 1/Eβ, β ~ 0.7)
- la loi de Bath, qui stipule que le rapport d'énergie entre le choc principal et la plus grande réplique est de l'ordre de 30.
- la loi d’Omori-Utsu, qui donne la distribution en temps des évènements : la fréquence des répliques décroit comme l’inverse du temps écoulé depuis le choc principal (f ~ 1/tp, p ~ 1 à 1.4)
- la loi de productivité, qui relie le nombre de répliques produites à l’énergie du choc principal: Nrep ~ Eα, α ~ 0.5.
Ces lois ont permis la mise en place de modèles probabilistes de prévision de l’endommagement des structures ou la sismicité des failles tectoniques [2]. Elles restent cependant toujours empiriques et considérées comme une propriété émergente de la dynamique collective de nucléation des microfissures. Les systèmes réels, soumis à l'influence de facteurs externes dont il est souvent très difficile de maitriser tous les paramètres, s'avèrent cependant redoutablement complexes.
L'étude de systèmes modèles en laboratoire permet alors une meilleure maitrise du problème, permettant de pousser l'analyse à la recherche des origines profondes des lois statistiques observées. Ainsi, pour des solides sollicités en tension considérés ici, il est possible de ramener le problème à celui de la déstabilisation d’une unique fissure préexistante**, pour lequel il existe aujourd'hui un cadre théorique performant permettant d’aborder le problème d'un point de vue mécanique et statistique [3].
* En sismologie, l’intensité des tremblements de terre s’exprime généralement en termes de magnitude, M. Celle-ci est proportionnelle au logarithme de l’énergie et la loi de Gutenberg-Richter est usuellement présentée sous la forme log10 N=a-bM avec b~1.
** La situation est radicalement différente sous compression : le matériau commence par s’endommager par événements successifs de microfissuration, puis s’effondre brutalement lorsqu’une fissure macroscopique traverse le matériau endommagé..
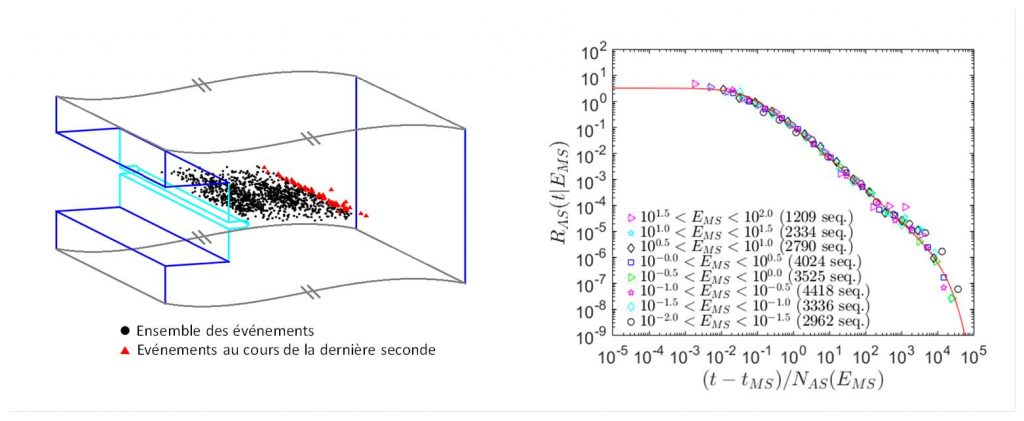
À droite : De façon similaire aux évènements sismiques, les événements acoustiques s’organisent pour former des séquences de répliques caractéristiques obéissant à des lois bien particulière (ici selon la loi d’Omori-Utsu unifié, reliant, en fonction de l'énergie du choc principal EMS , le taux de production de réplique RAS au temps passé depuis de choc principal, t-tMS)
Dans ce contexte, une équipe du SPEC/SPHYNX, en collaboration avec des chercheurs du CNRS, a analysé l’émission acoustique produite lors de la très lente propagation (typiquement 10 cm en 5h) d'une fissure unique au sein d'une roche artificielle de microstructure modulable [4]. Cette expérience permet de s'affranchir de l'influence de paramètres extérieurs, et son analyse montre sans ambiguïté une organisation en séquences de répliques obéissant aux quatre lois sismiques présentées ci-dessus. Cette étude modèle de la propagation d’une fissure unique possède notamment le grand avantage de présenter une certaine stationnarité statistique, qui permet de comprendre l'origine de ces lois, et de les relier entre elles. On démontre ainsi que la loi de productivité, gérant le nombre de répliques, et la loi de Bath, gérant l'énergie de ces répliques, sont une conséquence directe de la loi de Gutenberg-Richer ; la loi d’Omori-Utsu traduit quant à elle la distribution particulière – invariante d’échelle – des temps d’attente entre événements successifs. Le lien mis en évidence entre ces lois d'échelles, redécouvertes dans notre problème minimal de propagation de fissure unique, permet de conclure qu'il n'existe pas de corrélations cachées entre l'énergie des événements et leur temps d’occurrence, contrairement à ce qu’il est communément admis.
Stricto sensu les arguments précédents ne sont prouvés que pour la situation minimale considérée. Mais de façon surprenante, les relations obtenues entre les lois d'échelles se révèlent également compatibles avec les observations rapportées dans la littérature sur les problèmes bien plus complexes d’endommagement par multi-fissuration de matériaux en compression ; on peut alors conjecturer que ces systèmes doivent pouvoir se réduire à celui de la propagation d’une fissure unique.
Ces relations entre lois d'échelles ne sont en revanche pas vérifiées par les tremblements de terre. Leur compréhension et la statistique qui les régit restent encore bien plus complexes ! Une des difficultés pouvant être les interactions entre failles distinctes mais proches. Les équipes vont ainsi s'attacher à isoler les données pour des systèmes sismiques bien indépendants, afin de tester dans quelle mesure, la compréhension des lois statistiques en fracture des matériaux peut s'étendre à la sismologie.
Références :
[1] Référence récente dans le domaine :
« Statistical similarity between the compression of a porous material and earthquakes »
J. Baro, Á. Corral, X. Illa, A. Planes, E. K. H. Salje, W. Schranz, D. E. Soto-Parra and E. Vives, Phys. Rev. Lett. 110, 088702 (2013).
[2] « Statistical models for earthquake occurrences and residual analysis for point processes »
Y. Ogata, J. Am. Stat. Assoc. 83, 9 (1988)
[3] « Dynamics of cracks in disordered materials »
D. Bonamy, C. R. Physique 18 297–313 (2017).
[4] « Aftershock sequences and seismic-like organization of acoustic events produced by a single propagating crack »
J. Barés, A. Dubois, M.L. Hattali, D. Dalmas & D. Bonamy, Nature Communication (2018) 1253.
Contact CEA-IRAMIS : Daniel Bonamy, Systèmes Physiques Hors-équilibres hYdrodynamiques éNergie et compleXité (SPHYNX), SPEC – UMR 3680 CEA-CNRS, Université Paris-Saclay.
Collaboration :
- J. Barés, A. Dubois, M.L. Hattali, D. Bonamy, groupe SPHYNX au SPEC, UMR 3680 CEA-CNRS, Université Paris-Saclay, CEA Saclay 91191 Gif-sur-Yvette Cedex, France
- D. Dalmas, Laboratoire de Tribologie et Dynamique des Systèmes (LTDS), CNRS, École Centrale Lyon, 69134 Ecully Cedex, France
Affiliation actuelle des auteurs :
- SPEC, CEA, CNRS, Université Paris Saclay 91191 Gif sur Yvette France
- LTDS, CNRS, Ecole Centrale Lyon, 69134 Lyon France,
- LMGC, Université de Montpellier, CNRS, 34090 Montpellier France
- Laboratoire FAST, Université Paris Sud, CNRS, Université Paris-Saclay, F-91405 Orsay France.