L'énergie mécanique injectée dans un fluide visqueux se dissipe sous forme de chaleur par l'effet de la viscosité. Cette conversion est extrêmement complexe, et s’opère via des mouvements tourbillonnants sur une large gamme d’échelles. Les physiciens pensent que ce processus est bien décrit par les équations de Navier-Stokes. Si ces équations semblent bien décrire les mouvements des fluides, les mathématiciens, eux, ont des doutes concernant leur validité : ces équations sont-elles bien posées ? Leur solution est-elle unique ? Ne pourraient-elles receler des singularités, pour lesquelles la vitesse deviendrait localement spontanément infinie ? Et avec quelles conséquences sur la dissipation d’énergie ?
L'équipe SPHYNX du SPEC, apporte une première réponse expérimentale à certaines de ces questions en utilisant un dispositif expérimental permettant de mesurer localement, et avec une très grande précision, la vitesse du fluide et donc les transferts d’énergies jusqu'à l’échelle où la viscosité opère. On observe l'émergence d’événements intenses de dissipation d’origine non-visqueuse, qui pourraient être associés aux singularités mathématiques recherchées par les mathématiciens. Ce résultat impose de fortes contraintes sur la taille des échelles à résoudre pour espérer effectuer une simulation fidèle des fluides réels et pourrait bouleverser certaines méthodes numériques.
Dans la nature, de nombreux phénomènes impliquent le mouvement de fluides visqueux, qui peuvent être décrits par les équations fondamentales de Navier-Stokes (NS). Ces équations aux dérivées partielles traduisent les lois de conservation de la masse, de la quantité de mouvement et de l'énergie. Elles sont à la base des simulations numériques de dynamique des fluides dans des domaines aussi variés que l'aéronautique, l'astrophysique ou les études sur le climat. L'enjeu économique associé à ces études est aussi non négligeable, les pertes énergétiques induites par les effets de turbulence (transports terrestre, maritime et aérien, sources d'énergies éolienne ou hydrolienne, …) étant considérables.
Une question centrale, commune à tous ces domaines, est de décrire correctement la dissipation d'énergie au cours de l'écoulement d'un fluide. Sous l'action de forces extérieures, le fluide devient turbulent, et se structure en mouvements tourbillonnaires sur une gamme d’échelles pouvant couvrir plusieurs ordres de grandeur. L'énergie mécanique à l'origine du mouvement global est ainsi transférée vers des structures de plus en plus petites, pour être finalement dissipée sous l'effet de la viscosité, aux plus petites échelles, pour lesquelles le nombre de Reynolds Re [i] est typiquement de l'ordre de 1 (échelle de Kolmogorov).
Pour simuler numériquement le comportement des fluides et cette conversion d’énergie, il est crucial de savoir si les équations de Navier-Stokes sont bien posées : une solution obtenue à un instant t reste-t-elle régulière ou au contraire développe-t-elle des singularités après un temps fini ? La réponse à cette question reste pour l’instant un problème ouvert, à tel point que la preuve de l’existence de solutions de NS globalement régulières en dimension 3 a été identifiée comme l’un des 7 défis du millénaire par le Clay Mathematics Institute (CMI), dotés chacun d'un prix de 1 million de $.
[i] Le nombre de Reynolds est donné par Re = VL/ν, avec V et L, la vitesse et une dimension, caractéristiques de l'échelle considérée dans l'écoulement, et ν la viscosité cinématique.
Une des preuves indirectes de l’existence de singularités dans NS pourrait provenir du comportement du taux de dissipation de l’énergie quand le nombre de Reynolds devient très grand. Depuis les expériences de Taylor (1934), on sait en effet que cette quantité sature et devient indépendante de la viscosité dans la limite des faibles viscosités ν (i.e. pour les grands nombres de Reynolds). En 1940, Lars Onsager a proposé de relier cette observation à l’existence de singularités de la vitesse, qui produiraient une dissipation « inertielle », indépendante de la viscosité. Ce n’est qu’en 2000 que deux mathématiciens français, Jean Duchon et Raoul Robert [3], ont réussi à calculer l’expression de ce type de dissipation, en utilisant le formalisme développé dès 1934 par Jean Leray. La mesure expérimentale de cette dissipation inertielle dans un écoulement turbulent s’est cependant heurtée pendant longtemps à des difficultés techniques, du fait de la difficulté de mesurer le champ de vitesse sur une gamme d’échelles et de positions suffisamment étendue. Le développement récent de méthodes de mesure des champs de vitesse d'un fluide (méthode « Particle Image Velocimetry »), sur des échelles allant du décimètre au millimètre et couvrant la gamme de fréquence 1Hz – 1kHz, permet aujourd'hui de surmonter cette difficulté [1].
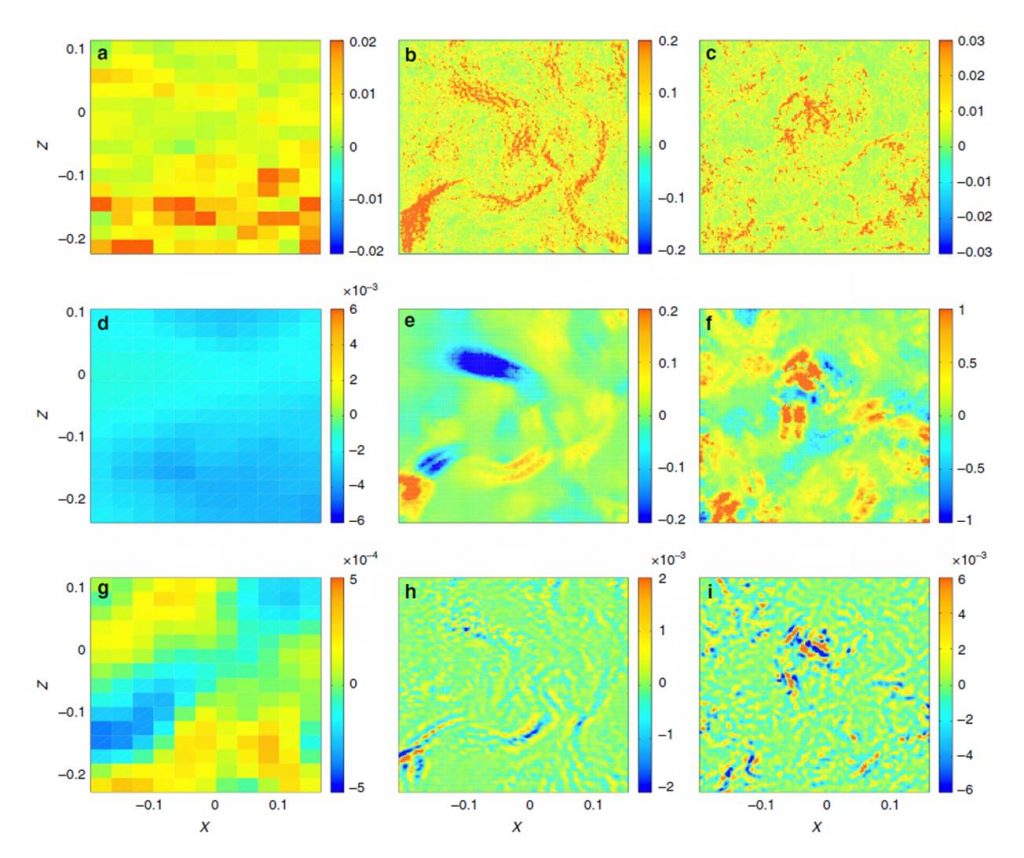
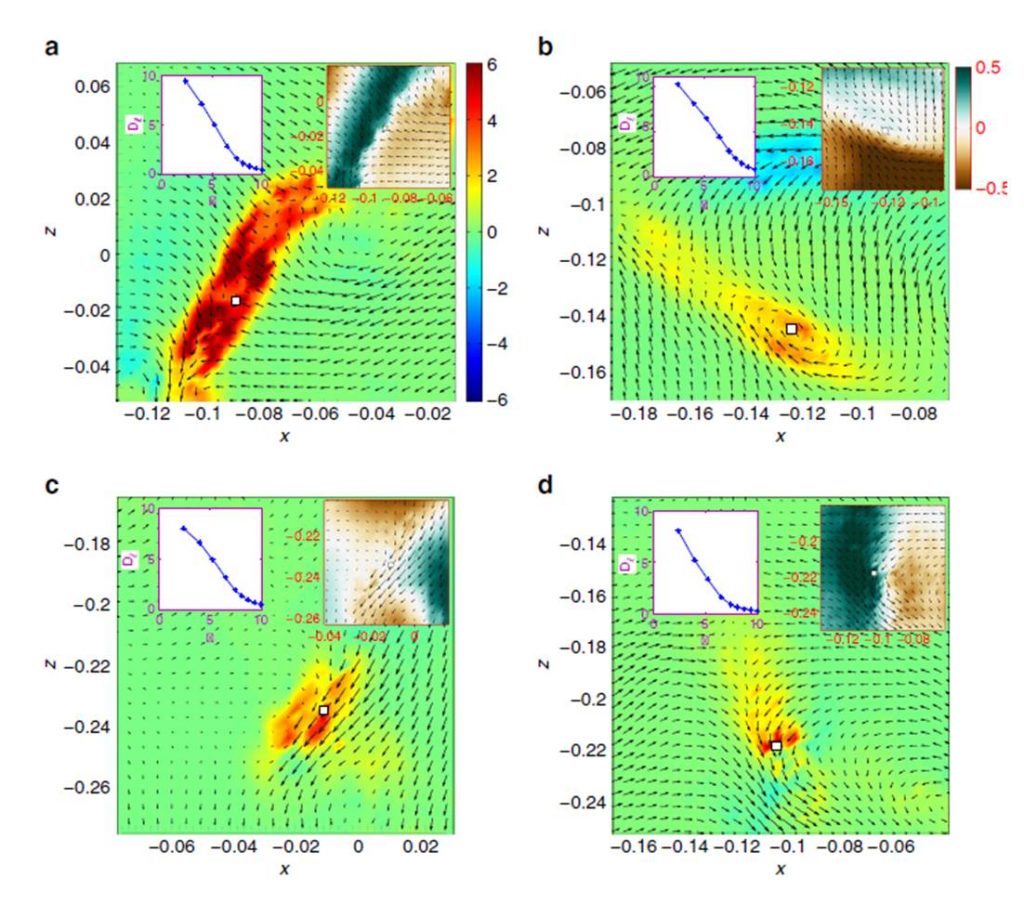
C’est en utilisant cette technique que l'équipe SPHYNX de l'IRAMIS/SPEC vient de réaliser la première mesure expérimentale quantitative de dissipation inertielle dans un écoulement turbulent tourbillonnaire [2]. Les mesures montrent pour la première fois, l’émergence d’événements extrêmes de dissipation non visqueuse, à des échelles où la viscosité est censée amortir tout mouvement et dissiper toute l’énergie. De façon surpenante, les champs de vitesses correspondants à ces événements extrêmes peuvent être classifiés en un petit nombre de variétés topologiques : 4 classes de champs de vitesses ont été observées, allant de « fronts » (analogues aux fronts observés en météorologie), aux spirales en passant par des jets, ou des « cusps » (voir figure). Ces structures pourraient correspondre à des pré-singularités, des événements précurseurs des singularités à petite échelle recherchées par les mathématiciens.
Ces observations bien caractérisées sont une étape utile sur la longue route qui mène vers la solution du défi Clay portant sur l'équation de Navier-Stockes. Elles soulignent la nature non-triviale des mouvements et des transferts d’énergie aux différentes échelles dissipatives, et imposent de fortes contraintes sur la gamme d'échelles où une solution doit être obtenue, pour espérer effectuer une simulation fidèle des fluides réels.
Références :
[1] New criteria to detect singularities in experimental incompressible flows
D. Kuzzay, E.-W. Saw, J. W. A. Martins, D. Faranda, J.-M. Foucaut, F. Daviaud, B. Dubrulle, arXiv:1601.03922 (2016).
[2] Experimental characterization of extreme events of inertial dissipation in a turbulent swirling flow,
E.-W. Saw, D. Kuzzay, D. Faranda, A. Guittonneau, F. Daviaud, C. Wiertel-Gasquet, V. Padilla & B. Dubrulle, Nature Communication, 12466 (2016), 31 Août 2016.
[3] Inertial energy dissipation for weak solutions of incompressible Euler and Navier-Stokes equations
J. Duchon and R. Robert, Non linearity 13 (2000) 249.
Voir le Communiqué de presse CEA-CNRS : « Mieux maîtriser la turbulence : première observation d'événements singuliers de dissipation de l'énergie » (sur le site du CNRS).
Contact SPEC : Bérengère Dubrulle et et François Daviaud (IRAMIS/ SPEC – UMR 3680 CEA-CNRS / SPHYNX).
Affiliations des auteurs :
- SPEC, CEA, CNRS, Universite´ Paris Saclay, CEA Saclay, 91191 Gif-sur-Yvette, France.
- LSCE, IPSL, CEA-CNRS-UVSQ, Universite´ Paris-Saclay, 91191 Gif-sur-Yvette, France.
- ENS Lyon, Lyon, France.