Une fracture sous l'effet d'une contrainte peut se propager de façon continue ou intermittente, et il est technologiquement très utile de pouvoir prédire dans quel régime se produira la propagation d'une éventuelle fissure. Par une approche statistique, une description globale des deux régimes a pu être obtenue, ainsi que le diagramme de phase précisant leurs conditions d'apparition. De plus, l'étude montre que les deux régimes sont de nature profondément différente : le régime intermittent présente des fluctuations à toutes les échelles de temps, ce qui rend la dynamique de fissuration imprévisible, quelle que soit l’horizon choisi.

Du point de vue de l'ingénieur, les études de fracture sont usuellement traitées par la mécanique des milieux continus , qui relie de façon déterministe la dégradation d'un matériau à la charge qui lui est appliquée. Cette idéalisation est pertinente dans la plupart des situations. Ces méthodes sont aujourd'hui largement utilisées pour dimensionner les structures et prévoir leur durabilité (ex : logiciel CAST3m développé par le CEA pour l’analyse des structures).
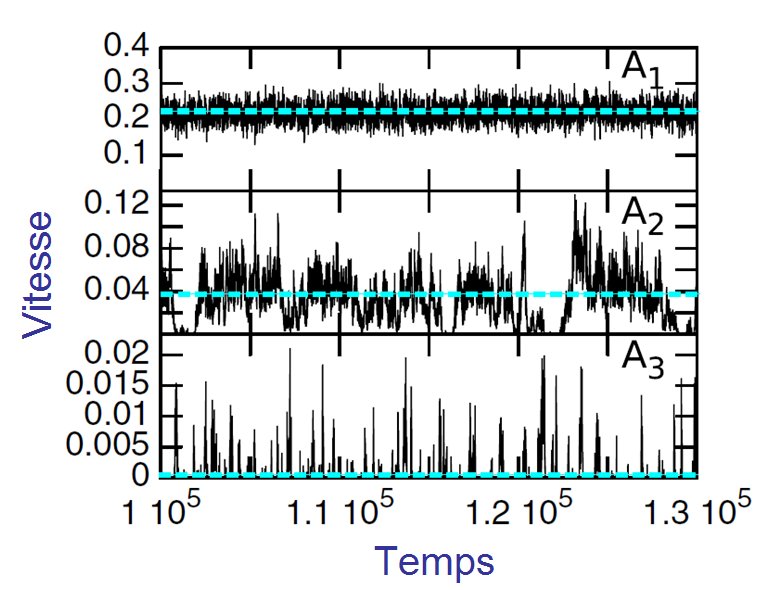
Sous l'application d'un chargement graduel, on peut observer de façon commune l'avancée apparemment continue d'une fissure dans un matériau, mais aussi, sous certaines conditions, une avancée intermittente, souvent perceptible par les craquements émis.
Les modèles continus peuvent a priori rendre compte de l'avancée continue ou intermittente d'une fissure, mais ne peuvent, et ceci est un principe fondamental, conduire qu'à des dynamiques de propagation avec une vitesse moyenne de propagation de la fissure bien définie. Autrement dit, où l'on peut oublier tous les détails sur la propagation à l'échelle élémentaire, et en particulier lisser l'intermittence à petite échelle de la dynamique.
Dans le régime de fracture intermittent des matériaux, l'analyse statistique de la propagation montre une distribution des évènements (notamment les tailles et durées des avancées) en loi de puissance (de même que la loi de Richter-Gutemberg en sismologie, donnant le nombre de tremblements de terre d'intensité supérieure à une magnitude donnée). Les fissures se propagent ainsi par des sauts aléatoires discrets distribués sur plusieurs ordres de grandeur en taille et en temps, ne permettant plus de définir un temps ou une taille caractéristique de lissage de l'intermittence. Seule une approche statistique peut alors permettre de rendre compte de ce type de dynamique.
L'équipe » Systèmes complexes et fracture » du SPCSI a développé un modèle, qui permet de préciser les conditions d'apparition de chaque régime et de décrire dans un formalisme unifié ces deux comportements apparemment très distincts. Ce modèle est basé sur une équation générique, pouvant décrire la propagation de fissure en mécanique linéaire de la rupture, où le caractère hétérogène du matériau (inhomogénéités à l'échelle de la microstructure avec une distribution spatiale aléatoire) est pris en compte sous la forme d'un terme de bruit d'énergie de fracture, de granulométrie imposée.
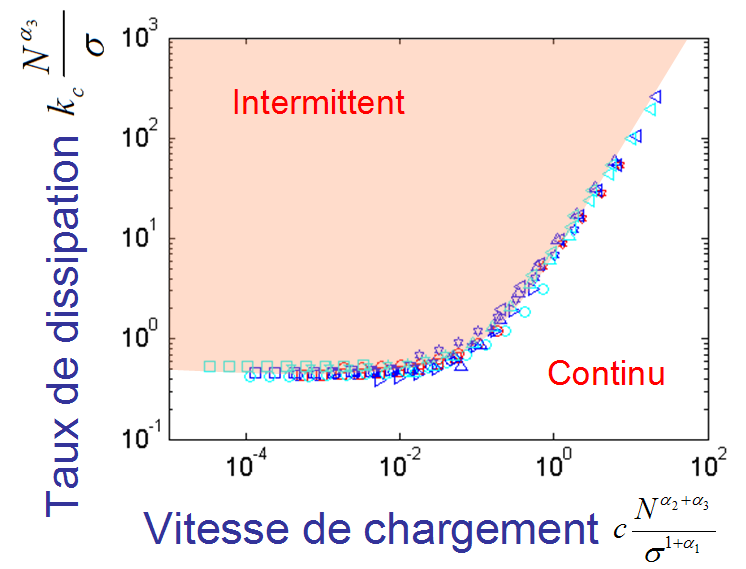
L'analyse statistique des résultats de simulations (solution de l'équation différentielle par une méthode de Runge-Kutta d'ordre 4) permet de distinguer les deux régimes : continu et intermittent. Ceci permet de définir dans l'espace des paramètres (vitesse de chargement – taux de dissipation) un diagramme de phase complet séparant les deux régimes de propagation (voir figure). Ainsi un désordre microstructural important (grand σ, petit N), une petite taille d'échantillon (N), une faible vitesse de chargement (c), et une forte valeur du facteur de relaxation élastique (k) lors de l'avancée de la fissure favorisent l'intermittence. Ce diagramme, présenté ici en coordonnées réduites, montre bien toute la généralité de la solution obtenue.
La distinction profonde de nature entre les deux régimes a pu aussi être précisée. L'examen détaillé de la vitesse de fracture (étude par transformée de Fourier), montre que les variations de taux de dissipation (k) affectent dans le régime intermittent toutes les échelles de temps : le spectre présente une même loi de puissance, dont le préfacteur est fonction de k. Dans le régime continu, des variations similaires n'affectent que l'échelle la plus grande. Le passage d'un type de comportement, directement relié au régime d'avancée de la fissure, à l'autre, est abrupt, ce qui montre bien que l'on est face à une vraie transition.
Ces résultats éclairent les processus de fracture technologiques (ex : en technologies de découpe des matériaux) et pourront permettre le développement futur de méthodologies de conception rationalisée pour éviter (ou limiter) les phénomènes de fracture intermittente inopportuns et les indéterminations associées. L'analogie entre le régime décrit et celui des tremblements de Terre mérite aussi d'être exploré plus avant, en précisant en particulier la nature des régimes précurseurs et de répliques aux évènements extrêmes, indispensable avant toute prédiction dans ce domaine.
Référence :
Crackling versus continuum like dynamics in brittle failure
J. Barés, L. Barbier, and D. Bonamy, Phys. Rev. Lett. 111 (2013) 054301.
Contact CEA : Daniel Bonamy.





