Bulles de savon et calcul variationnel
Plan du cours
- Qu’est-ce qu’une EDP ?
- Généralités sur les EDP EDP linéaires du premier ordre
- Classification des EDP linéaires du 2nd ordre à coefficients constants
- Conditions aux frontières et problème bien posé.
- Équation des ondes
- Équation de diffusion
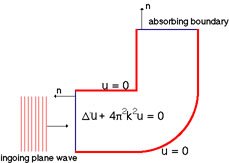
- Équation de diffusion sur un domaine spatial borné Solution fondamentale de l’opérateur de Helmholtz dans R2.
- Espace fonctionnel
Équations différentielles du premier ordre: équation de Burgers et onde de choc.
- Notions d’intégrale première.
- définition.
- exemple simple et généralisation.
- Méthode des caractéristiques.
- théorème des fonctions implicites.
- équations aux intégrales premières et interprétation géométrique.
- principe de la méthode des caractéristiques.
- conditions au bord / condition initiale.
- Équation de Burgers.
- système caractéristique et intégrale première.
- problème d’inversion.
- Écoulement unidimensionnel de particules sans interaction.
- le modèle.
- résolution de l’équation.
- notion d’onde de choc.
Équation de sine-Gordon, solitons et dislocations.
- Équation de sine Gordon.
- la chaine de pendules couplés.
- équations du mouvement.
- passage au continu: équation de sine Gordon
- Solutions de l’équation de sine-Gordon.
- les solutions de faible amplitude.
- les solutions soliton.
- énergie du soliton.
- Dislocations dans les cristaux.
- modèle d’interaction atomique unidimensionnel.
- passage au continu et profil des déplacements.
- énergie de la dislocation.
Diffusion par un milieu inhomogène
- Équation de Helmholtz et fonction de Green.
- les ondes planes.
- fonctions Green de l’équation de Laplace.
- ondes sortantes et rentrantes.
- Solution générale de l’équation de diffusion.
- Théorème de Green.
- solution générale
- condition de rayonnement et formule intégrale de la diffusion.
- Comportement asymptotique.
- Première approximation de Born.




