contact: F. Ladieu
Lorsqu’il est trempé sous sa température de transition vitreuse Tg, un verre se met à vieillir : ses propriétés se mettent à dépendre de son âge ta, c’est-à-dire du temps écoulé depuis le franchissement de Tg. Comme les verres forment une très vaste catégorie (verres à vitres, polymères, colloïdes, bouteilles en plastiques…), ce phénomène de vieillissement concerne a priori un grand nombre de nos matériaux « du quotidien ». En dépit de son ubiquité, le vieillissement est pourtant fort mal compris, en particulier du fait d’absence de consensus sur ce qui se produit microscopiquement lors du vieillissement. Nous avons réussi à montrer [1], pour la première fois, que le vieillissement s’accompagne d’un accroissement du nombre de molécules dont les mouvements sont corrélés : ceci permet de mieux caractériser par quels aspects le verre, en dessous de Tg, est un solide, et par quels aspects il reste néanmoins un liquide.
Il est bien difficile de comprendre pourquoi, lorsqu’ils sont refroidis, certains liquides « ratent » la cristallisation à la température prévue Tm et restent dans un état de liquide surfondu. En poursuivant le refroidissement, cet état liquide voit sa viscosité (ou son temps τα de relaxation moléculaire) augmenter vertigineusement, c’est-à-dire plus vite qu’une loi d’Arrhénius. Ceci suggère que des corrélations entre molécules existent à des échelles de plus en plus vastes lorsqu’on diminue la température T. Pourtant aucun changement de structure ne peut se lire dans les spectres de diffusion des neutrons ou des rayons X qui restent globalement inchangés entre Tm et Tg, où Tg est la température de transition vitreuse définie par τα=100s.
Au cours des 15 dernières années, on a peu à peu compris que le moyen le plus simple de percevoir les corrélations vitreuses était de les rechercher dans les mouvements des molécules (et non pas dans leurs positions ou leurs orientations) : il est apparu plausible que la relaxation dans un liquide surfondu se fasse par paquets de Ncorr molécules dont les mouvements sont corrélés les uns aux autres. Un peu comme dans un métro bondé à l’heure de pointe, où les mouvements individuels sont impossibles et où seuls les mouvements de groupes d’individus sont permis (comme celui permettant de sortir du wagon en arrivant à destination !). Cependant, en mettant des ordres de grandeur raisonnables sur cette idée, on estime que Ncorr peut valoir 100 à Tg, ce qui correspond à une longueur typique de quelques nanomètres, extrêmement difficile à filmer ! Par ailleurs, ces corrélations étant d’un type nouveau, elles ne sont pas reliées à la fonction de corrélation usuelle à deux points et, en utilisant le théorème de Fluctuation Dissipation, elles ne sont donc pas reliées non plus à la fonction de réponse linéaire χlin usuelle (définie plus bas). On était donc devant une double difficulté (pratique et théorique) pour détecter et étudier les corrélations vitreuses.
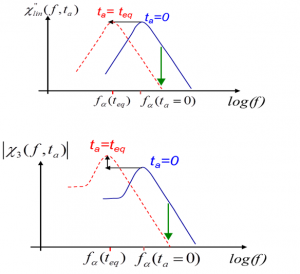
Fort heureusement, un travail théorique de J.-P. Bouchaud et G. Biroli a établi que la susceptibilité non linéaire (macroscopique !) χ3 était directement proportionnelle à Ncorr. Plus précisément si l’on applique un champ (électrique) au liquide de fréquence f, sa réponse (polarisation) s’écrit P = χlinE+ χ3E3, et selon la prédiction précitée χ3(f,T) ~ Ncorr(T)*H(f/fα(T)) où fα(T)=1/τα(T) et où la fonction H a une forme en cloche décrite sur le bas de la figure 1. La fonction H ne dépendant pas de la température T, même si elle n’est pas analytiquement connue pour un liquide donné, on peut, en mesurant χ3 à différentes fréquences et températures, avoir accès à l’évolution relative de Ncorr avec T : c’est ce que nous avons fait dans les références [2-3] à l’équilibre (T>Tg), ce qui a permis de montrer que, au-dessus de Tg, Ncorr augmente significativement dans le Glycérol lorsqu’on diminue T vers Tg. Ceci pourrait être l’origine microscopique du comportement super-Arrhénien de τα.
Nous sommes parvenus à pousser ces mesures de χ3 jusque dans le régime vieillissant, où après une trempe en Température de T>Tg à T<T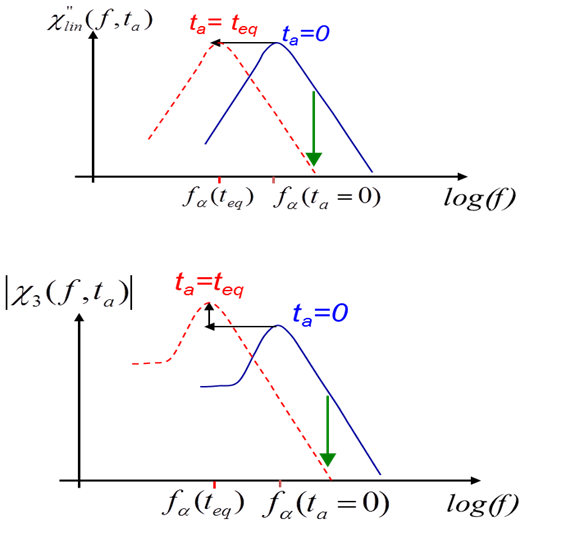
Cette observation directe, qui est une première du genre, a plusieurs conséquences importantes :
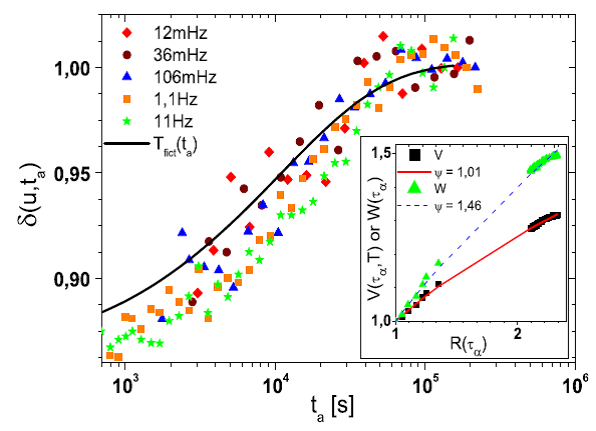
1. L’augmentation constatée de Ncorr avec l’âge est très similaire à celle qu’on aurait pu extrapoler à partir des résultats obtenus à l’équilibre (T>Tg), en utilisant la notion de température fictive Tfict(ta) : sans entrer dans les détails de ce concept, signalons seulement que cela donne la courbe noire qui est très proche des points mesurés pour δ. Ceci montre que le verre au-dessous de Tg a les propriétés d’un liquide. Cette conclusion –surprenante au premier abord- est renforcée par une constatation très simple : le vieillissement s’arrête au bout d’un temps fini dans le Glycérol et Ncorr garde une valeur finie : ceci est caractéristique d’un liquide. Dans un solide, en effet, le vieillissement durerait un temps infini, ce qui correspondrait à l’établissement de corrélations concernant le système entier (et donc à Ncorr tendant vers l’infini).
2. Cependant cet état liquide du verre au-dessous de Tg n’est pas n’importe quel état liquide : il s’agit d’un liquide comportant des corrélations tout à fait non triviales où les évènements de relaxation mobilisent un nombre Ncorr de molécules : ces corrélations donnent une connotation « solide » au système. La théorisation de cet état liquide très particulier a donné lieu à de nombreuses théories dans la littérature. Nos expériences de vieillissement, une fois jointes aux mesures faites à l’équilibre, sondent un très grand nombre de décades de τα: cela nous a permis de tester efficacement certaines des théories proposées. Sans entrer dans les détails, l’insert montre que deux d’entre elles survivent à la confrontation avec nos expériences, car on peut rendre compte de nos données (points verts ou noirs) en utilisant des exposants proches de ceux qui sont prédits (courbe rouge ou pointillés bleus). Au moins une autre théorie est réfutée par nos mesures, car elle ne peut rendre compte de nos données que par le truchement d’une valeur non physique de l’exposant.
[1] C. Brun, F. Ladieu, D. L’Hôte, G. Biroli, J.-P. Bouchaud, Phys. Rev. Lett. 109, 175702 (2012).
[2] C. Crauste-Thibierge, C. Brun, F. Ladieu, D. L’Hôte, G. Biroli, J.-P. Bouchaud, Phys. Rev. Lett. 104, 165703, (2010).
[3] C. Brun, F. Ladieu, D. L’Hôte, M. Tarzia, G. Biroli, J.-P. Bouchaud, Phys. Rev. B 84, 104204 (2011).