K. Katsuyoshi, D. L’Hôte, S. Nakamae, M. Konczykowski, V. Mosser
Le théorème de fluctuation-dissipation, reliant l'intensité des fluctuations d'une observable à la réponse à une sollicitation, est un principe vérifié pour tous les systèmes à l'équilibre thermodynamique. Une collaboration de chercheurs de l'IRAMIS/SPEC et LSI a étudié un système ferrofluide, formé d'un ensemble de nanoparticules magnétiques en suspension dans un liquide, et montré qu'il ne satisfait plus ce théorème de fluctuation-dissipation à très basse température dans sa phase gelée, en dessous de sa température de transition (Tg = 67K) entre un état superparamagnétique (à l'équilibre) et un état de verre de superspins (à dynamique lente). Cette première démonstration de la violation du théorème de fluctuation-dissipation sur ce système original enrichit le domaine très actif de la physique statistique des systèmes hors d’équilibre.Le théorème fluctuation-dissipation (TFD) est un des résultats les plus fondamentaux de la physique statistique. Il relie l'intensité des fluctuations thermiques d’un système en équilibre à sa réponse à une force extérieure. Il traduit le fait que l’énergie apportée par cette force sera dissipée en chaleur en raison du caractère erratique et fluctuant des interactions avec les composants microscopiques du système. Sa version la plus célèbre est l’équation d’Einstein qui relie le coefficient de diffusion D d’une particule Brownienne dans un fluide (D « mesure » les fluctuations thermiques) à la viscosité η du fluide (η est la « réponse » du fluide à une force s’exerçant sur un objet en mouvement).
Dans sa forme générale, ce théorème relie le spectre Sx(w) des fluctuations δx d’une observable x, à la partie dissipative de la susceptibilité χ”(w) qui traduit la réponse au champ conjugué à cette observable.
où ω/2π est la fréquence et T la température.
Le TFD s'applique aux systèmes à l’équilibre. Durant les trois dernières décades, son extension au cas hors d’équilibre a fait l’objet de nombreuses recherches expérimentales et théoriques [1]. Selon certains modèles, le TFD peut être conservé dans le cas hors d’équilibre à condition de remplacer la température T par une température effective Teff supérieure, le rapport (Teff / T) donnant une mesure de l’écart à l’équilibre du système. Pour tester cette prédiction, les verres sont des systèmes physiques idéaux car ils sont par nature hors d’équilibre et à dynamique lente. Parmi ces systèmes, un verre de spin est un ensemble de moments magnétiques désordonnés interagissant entre eux. Pour baisser l’énergie d’un spin donné, il ne suffit pas de le réorienter, mais il faut aussi réorienter ses voisins, puis les voisins des voisins, etc… Il faut donc un temps très long pour atteindre l’équilibre.
L’étude de la violation du TFD a concerné divers système vitreux jusqu’à ce jour, mais peu de résultats expérimentaux existent du fait de la difficulté à mesurer les faibles signaux de « bruit » à l'origine des fluctuations d’une observable. L’équipe MFD ('Magnétisme, Frustration et Désordre') de l'IRAMIS/SPEC dans le cadre d’une collaboration avec une équipe du LSI, a ainsi testé le théorème fluctuation-dissipation sur un verre de spin bien particulier : un ensemble de nanoparticules magnétiques (γ-Fe2O3) en suspension dans un liquide (ferrofluide) gelé car refroidi à basse température [2]. Chaque nanoparticule est monodomaine et porte un moment magnétique ~ 104μB très supérieur aux moments magnétiques atomiques, formant ainsi un « verre de superspins ». La température est choisie inférieure à la température de transition Tg = 67K où le système passe de l’état superparamagnétique (aimantation fluctuante des grains individuels, à l'équilibre) à l’état verre de superspins. Dans ce système, les interactions dipolaires entre moments magnétiques sont à l’origine des propriétés de verre de spin avec une dynamique lente et des effets de mémoire.

Expérimentalement, les fluctuations de l’aimantation d’un échantillon de ce ferrofluide ont été mesurées à l’aide d’un capteur à effet Hall. Sa partie conductrice est un gaz d’électrons à deux dimensions (2DEG : two-dimensional electron gas) piégé dans un puits quantique (hétérostructure AlGaAs/InGaAs/GaAs) ayant une surface sensible au champ magnétique de 2×2 μm2. Une goutte de 7 picol de ferrofluide de diamètre ~ 30 μm) est déposée au dessus de cette zone sensible (figure 1). Afin d’améliorer la sensibilité de la sonde de Hall, la technique du « spinning current » (ou compensation dynamique des tensions d'offset) [3] a permis de s'affranchir du bruit parasite due à la sonde ou à l’environnement.
Les fluctuations du champ mesuré Bz (de spectre S(ω,T)) sont proportionnelles aux fluctuations d’aimantations de l’échantillon. Pour tester le TFD, chaque composante du spectre d'aimantation a été comparée à la susceptibilité à la fréquence ω : χ’’(ω,T) d’un échantillon de ferrofluide mesurée à l’aide d’un magnétomètre à SQUID [1]. Les deux mesures ont été réalisées après un même temps de « vieillissement » tw du verre de superspin, ce qui garantit un état hors d’équilibre identique. Le TFD prédit :
Où la Cste dépend du volume de l’échantillon et du lien entre Bz et son aimantation. La partie imaginaire de la susceptibilité, χ’’(ω,T), à une fréquence donnée est effectivement proportionnelle à S(ω,T)/T pour T>Tg = 67K. Mais le rapport de proportionnalité change pour T<Tg, le TFD, vérifié comme attendu dans la phase paramagnétique à l’équilibre à haute température, est violé dans la phase verre de spin à basse température. Le rapport de proportionnalité donne la température effective Teff évoquée ci-dessus.
[1] SQUID : « Superconducting Quantum Interference Device », magnéomètre constitué de boucles de supraconducteurs et de jonctions Josephson (supra/non supra/supra).

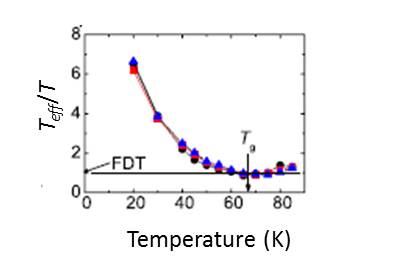
La fig. 2 présente le rapport Teff /T obtenu expérimentalement en fonction de T. Ce rapport augmente de façon monotone lorsque T diminue en partant de 1 pour T=Tg. Lorsqu’on baisse la température T, le système met des temps de plus en plus long pour se rapprocher de l’équilibre. Il n’est donc pas surprenant que le rapport Teff /T qui mesure l’écart à l’équilibre soit plus élevé.
En conclusion, nous avons montré expérimentalement que le théorème fluctuation-dissipation est violé dans un système de nanoparticules magnétiques en interaction dipolaire, dans l’état verre de superspins. Nous avons évalué quantitativement l’écart à l’équilibre à travers la température effective Teff. C’est la première fois qu’une telle mesure est réalisée sur un tel système. Les précédentes mesures de ce type concernaient des verres structuraux [4] ou un verre de spins classique [5] (déjà au SPEC !). La possibilité de montrer la violation du TFD sur ce système original enrichit le domaine très actif de la physique statistique des systèmes hors d’équilibre. L’étape suivante consistera à étudier la dépendance de Teff en fonction de tw, le temps écoulé entre le passage dans la phase verre de spin et la mesure. Le système tendant lentement vers l’équilibre, il est prédit que Teff (tw) doit diminuer en se rapprochant de T.
Contacts : Denis L’Hôte, Sawako Nakamae
Ces résultats sont le fruit d'un travail commun à 2 laboratoires de l'IRAMIS du SPEC et du LSI et d'une colaboration avec ITRON, France (V. Mosser) et le laboratoire PECSA, UMR 7195 CNRS, Université Pierre
et Marie Curie (E. Dubois, V. Dupuis et R. Perzynski).
[1] On the out-of-equilibrium relaxation of the Sherrington-Kirkpatrick model,
L.F. Cugliandolo and J. Kurchan, J. Phys. A 27 (1994) 5749.
Off-equilibrium glassy dynamics: a simple case,
S. Franz and M. Mézard, Europhys. Lett. 26 (1994) 209.
Energy flow, partial equilibration, and effective temperatures in systems with slow dynamics
L.F. Cugliandolo, J. Kurchan and L. Peliti, Phys. Rev. E 55 (1997) 3898.
[2] Experimental evidence for violation of the fluctuation-dissipation theorem in a superspin glass,
K. Komatsu, D. L’Hôte, S. Nakamae, V. Mosser, M. Konczykowski, E. Dubois, V. Dupuis and R. Perzynski,
Phys. Rev. Lett. 106 (2011) 150603.
[3] Dynamic low-frequency noise cancellation in quantum well Hall sensors (QWHS)
A. Kerlain and V. Mosser, Sensors and Actuators A 142 (2008) 528.
[4] Observation of fluctuation-dissipation-theorem violations in a structural glass
T.S. Grigera and N.E. Israeloff, Phys. Rev. Lett. 83 (1999) 5038.
Off equilibrium fluctuations in a polymer glass
L.Buisson and S. Ciliberto, Physica D 204 (2005) 1.
[5] Fluctuation-dissipation ratio of a spin glass in the aging regime
D. Hérisson and M. Ocio, Phys. Rev. Lett. 88, 257202 (2002),
Off-equilibrium fluctuation-dissipation relation in a spin glass
D. Hérisson and M. Ocio, Eur. Phys. J. B 40 (2004) 283.





