D. Bonamy and L. Ponson (SPCSI), D. Santucci (Fysik Institutt Oslo)
Fracture is a phenomenon of everyday life: it is observable at all scales of condensed matter, from the atomic scale (in nanostructures) to the scale of our planet marked by fractures in the continental plates. But, can we find a unifying model to describe the phenomenon?
The dynamics of fracture is complex. In an ideal elastic material, perfectly homogenous, the situation remains relatively simple by means of the Elastic Linear Mechanics: the crack front is a smooth line, crossing the material with a predictable trajectory and at a regular speed that is function of the solicitation in tension. Taking into account the inhomogeneities inherent in any material (microstructure heterogeneities, point defects, temperature…) the crack no more propagate continuously but by apparently unpredictable leaps, which imposes a statistical treatment of the problem.

At points of high cohesion , the progression of the crack may be locally blocked. The crack front line is then deformed and mechanical energy accumulates (such as during the period between 2 earthquakes) until allowing the crack to cross the blocking point. After its abrupt depinning, the front propagates freely until a new zone of high cohesion is met (pinning). The mechanical energy is dissipated in the creation of the two fracture surfaces and of damage at the crack front.
A dynamic equation was proposed by writing, as in the homogeneous case, that the local speed of the crack front is proportional to the excess energy defined by the difference between the available mechanical energy and the required energy to create the fracture surfaces and some damage. A noise term introduced a non-correlated random element to reflect the heterogeneous nature of the material. This disorder term induces a roughness of the fracture line and the local mechanical energy depends now of the relative position with respect to the other points of the front line: less energy is available at a point far ahead the average crack front that at a point far behind it. In this description, the breakdown of materials is akin to a critical phase transition between a stable phase where the immobile crack is trapped by defects in the material and a mobile phase where the available mechanical energy is sufficient to allow the spread of the crack.
The master equation belongs to the universality class of « pinning-depinning transition of a line in elastic interaction, embedded in a long-range random external potential. » This class, originally introduced by Joanny and De Gennes, well describes the dynamics of a wetting front or of a ferromagnetic domain wall. It is characterized by a number of critical exponents reflecting the scale invariance at the critical point of the transition. But, does this model correctly describe the fracture phenomenon as suggested by Gao and Rice in 1989?
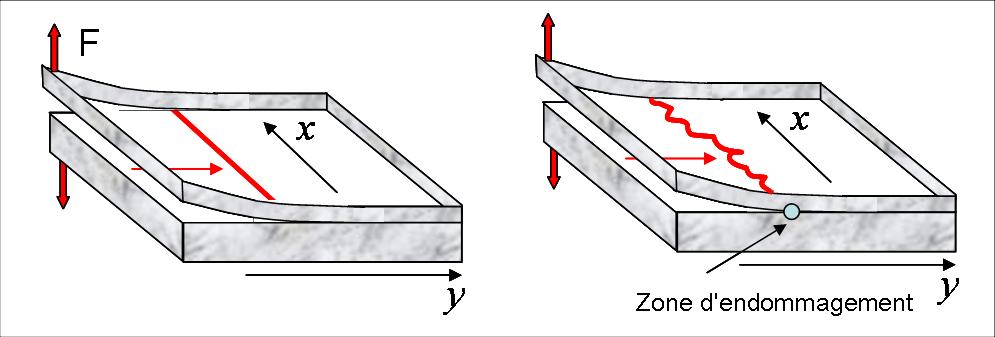
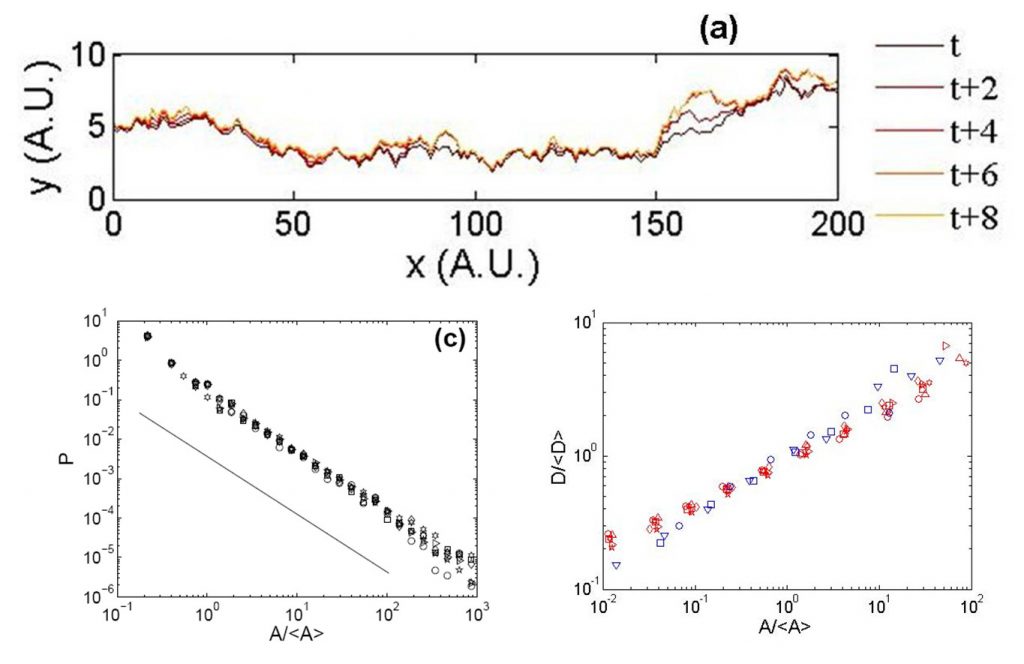
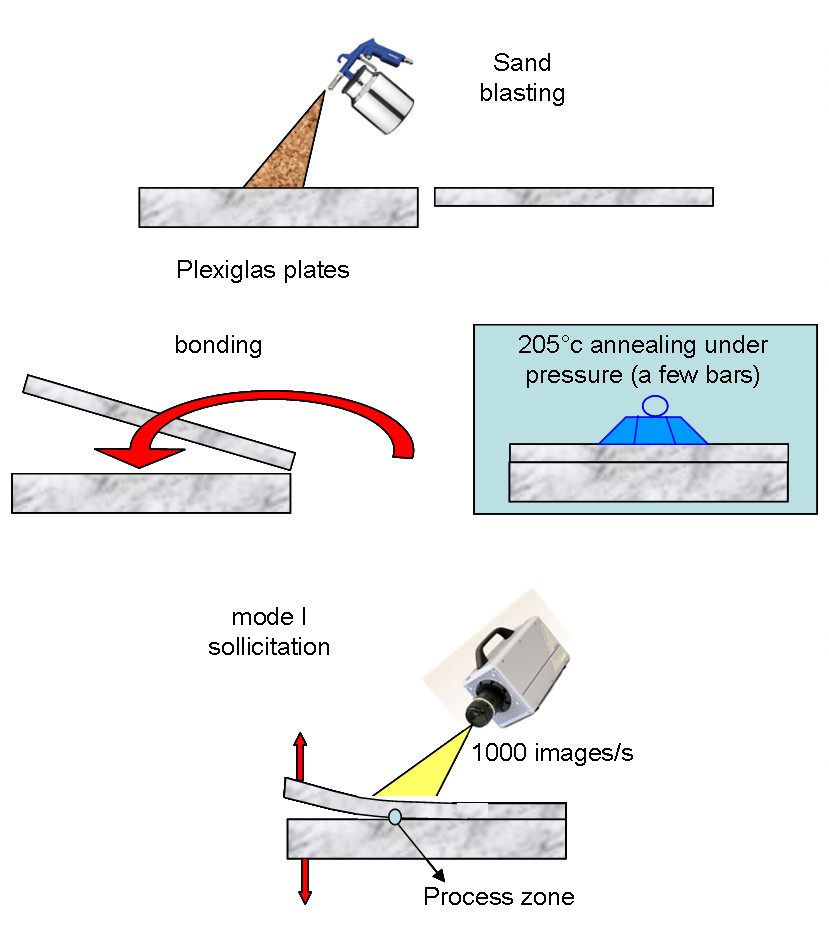
A model experiment performed at the Institute of Physics of Oslo, provides one answer to the problem. A two-dimensional interface is created by the blasting of two sheets of Plexiglass, then hot bonded under pressure. The material being transparent, the propagation of the crack front along this interface can be observed in time with a fast camera, allowing detailed statistical analysis of its spreading (morphology and local speed).
Simulations with the proposed model are first validated by recovering, as it should, the critical exponents, associated with the time fluctuations of the spatially averaged speed of the crack front, of the considered universality class. Unfortunately these critical exponents are difficult to measure experimentally. However, the very same simulations allows to retrieve other statistical quantities observed in the experiment, like the distribution of avalanches (see Fig.), giving thus evidence that the problem belongs to the « Joanny-De Gennes » universality class.
This provides a good model to describe the behavior of the critical propagation of a crack front. Without scale the model is not specific and must apply to any quasi-static fracture since the scale of nanostructures (such as the smart cut™ process of preparing plates of SOI, Silicon on oxide) to continental faults. For example, the very first analysis by the Oslo team of the time distribution of earthquakes is going that way. There is still much research work to validate the model on other systems, demonstrating its universal application, and beyond to extract for each realisation the non-universal associated quantities.
Crackling dynamics in material failure as the signature of a self organized dynamic phase transition
D. Bonamy, D. Santucci et L. Ponson, (SPCSI), Phys. Rev. Lett. sous presse,
K. J. Maløy, S. Santucci, J. Schmittbuhl and R.Toussaint, Phys. Rev. Lett. 96 (2006) 045501.
Le procédé « smart cut™ » (lien externe vers la Sté SOITEC).