Prévoir quand roches, ouvrages, structures et composants vont casser est un enjeu crucial. Pour les matériaux dits fragiles (verre ou porcelaine par exemple), la capacité d’un solide à résister à la fissuration est quantifiée par deux constantes matériau interdépendantes — l'une est proportionnelle au carré de l'autre — l'énergie de fracture et la ténacité. De fait, il existe à l’heure actuelle des essais expérimentaux bien établis qui permettent une détermination précise de ces constantes. En revanche, prévoir ab-initio leur valeur à partir des paramètres atomistiques du matériau considéré reste un problème largement ouvert, même dans les situations les plus simples ! La pierre angulaire dans ce contexte a été fournie par Alan Arnold Griffith[1]. Il propose d’identifier l’énergie de fracture, qui représente l’énergie mécanique à fournir pour que la surface d’une fissure augmente d’une unité, avec l’énergie spécifique de surface, qui correspond à l’énergie des liaisons chimiques traversées par cette unité de surface supplémentaire. Ce modèle suppose que l’on considère des matériaux parfaitement fragiles qui casseraient par rupture successives de liaisons chimiques sans impliquer de mécanismes de dissipation supplémentaires (écoulements plastiques ou visqueux, crazing dans les polymères…) Malheureusement, cette conjecture n’est pas en accord avec les observations: l’énergie de fracture apparaît toujours anormalement élevée, même dans les situations les plus fragiles (clivage du silicium ou du mica, par exemple).
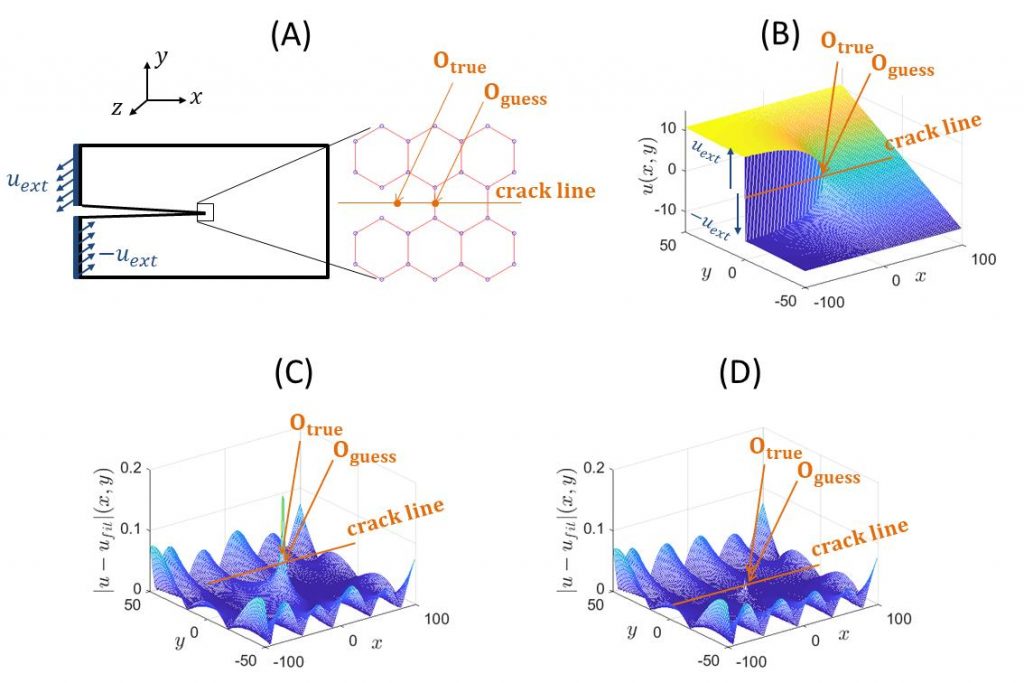
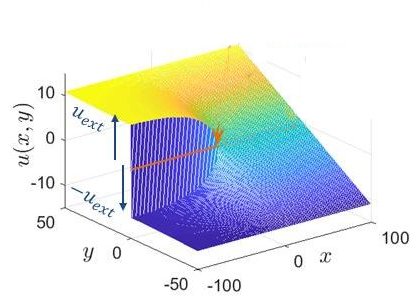
Panneau A : Une fissure est introduite dans un cristal électrique bidimensionnel en nid d’abeille. Elle est prise parallèle à l’axe x, au milieu du cristal (y = 0) et s’arrête au centre. Le cristal fissuré est alors sollicité en déplaçant perpendiculairement au plan les bords gauche/haut et gauche/bas du cristal d’une valeur constante, uext, mais opposée. Le champ de déplacement prend une forme asymptotique générique — singulière – en pointe de fissure (panneau B). Tout l’enjeu est de placer cette pointe sur le réseau atomique discret du cristal. Si on la place au centre de la prochaine liaison à casser (position Oguess sur panneau A), la forme singulière ajuste bien la carte de déplacements mesurée… sauf au voisinage de la pointe de fissure (panneau C). Malheureusement, c’est à cet endroit que la liaison se casse et qu’il est par conséquent important de connaître précisément le déplacement, les contraintes et les forces appliquées. Si maintenant cette pointe est positionnée judicieusement (position Otrue sur panneau A), l’ajustement est très bon partout, y compris au voisinage de la pointe de fissure (panneau D)
Pour comprendre l’origine de ce désaccord, des chercheurs de l’IRAMIS/SPEC/SPHYNX ont étudié par simulation numérique la propagation d’une fissure dans un réseau de fusibles électriques arrangés périodiquement. On peut en effet montrer que :
- les lois qui régissent la distribution des tensions et densité de courants dans ces réseaux électriques sont analogues aux lois de l’élasticité.
- ces « cristaux » électriques cassent de manière parfaitement fragile, par claquage successifs des fusibles, et les paramètres atomistiques sont parfaitement connus et modulables.
Sur ces simulations, l’énergie de fracture a été mesurée, et comme pour les matériaux réels, elle apparaît anormalement grande par rapport à la prédiction de Griffith, d’un facteur qui dépend de la géométrie du réseau.
L’analyse fine du champ de contrainte dans ces analogues électriques a permis de comprendre l’origine de ce désaccord. En réalité, ce n’est pas un bilan d’énergie qui sélectionne la résistance à rupture, mais la manière dont les champs continus de la mécanique (contrainte, déformation, déplacement) peuvent être raccordés à la nature discrète des solides à l’échelle atomique. Il est en effet établi, depuis les années 50 et les travaux d’Irwin [2] et Williams[3]que, dans un matériau élastique sous tension, le champ de contrainte diverge à la pointe d’une fissure. Du coup, toute erreur — aussi petite soit-t-elle – sur le positionnement de cette pointe dans le réseau atomique engendre des variations énormes sur la force ressentie par la liaison chimique sur le point de casser. Mais du fait même de cette divergence, le champ de contrainte prend mathématiquement une forme asymptotique générique au voisinage de la pointe [3], qui, pour un arrangement atomique de géométrie donnée, fixe précisément le positionnement de la pointe, et par conséquent la valeur de la ténacité du matériau. La mise en équation des éléments ci-dessus permet de déterminer théoriquement la résistance à la rupture (ténacité et énergie de fracture) des cristaux électriques et la valeur coïncide exactement avec la valeur obtenue par simulation numérique. L’analyse a été étendue au cas de « vrais » solides cristallins et fournit, par exemple, une prévision quantitative de l’énergie de fracture dans le graphène parfaitement compatible avec les mesures expérimentales. Au-delà du cas des solides « classiques », cette étude, publiée dans[4], fournit un premier jeu d’outils qui permettra de prévoir, l’effet de l’architecture sur la tenue à rupture de métamatériaux type treillis-(microlattices obtenus par fabrication additive) afin de l’améliorer et de l’optimiser. La finalité de ce travail est de développer une nouvelle gamme de matériaux à la fois ultralégers et résistants pour réduire l’empreinte carbone et la consommation énergétique des véhicules, dans le domaine du transport notamment. C’est dans cette voie que se lance maintenant l’équipe du SPEC/SPHYNX, en collaboration avec l’équipe LIONS de l’IRAMIS/NIMBE.
Références :
[1] « The phenomena of rupture and flow in solids »
A.A. Griffith., Phil. Trans. Royal Soc London A221, 123 (1920).
[2] « Analysis of stresses and strains near the end of a crack traversing a plate »
G. R. Irwin, Appl. Mech. 24, 361 (1957)
[3] « Stress singularities resulting from various boundary conditions in angular coners of plates in extension »
M. L. Williams, J. Appl. Mech. 19, 526 (1952)
[4] « Role of the Crystal Lattice Structure in Predicting Fracture Toughness »
T. Nguyen & D. Bonamy, Phys. Rev. Lett. 123, 205503 (2019)
Contact CEA-IRAMIS : Daniel Bonamy (SPEC – UMR 3680 CEA-CNRS/SPHYNX)
Collaboration : Thuy Nguyen & Daniel Bonamy. Thuy Nguyen est enseignante chercheur à l’EISTI et mène sa recherche au SPEC/SPHYNX.





