Below are listed my main research themes. References and preprints/ reprints can be found in my publication list.
Protoplanetary Nebula
It is commonly accepted that the solar system was formed from an accretion disk, called the protoplanetary nebula (see figure). The evolution of this disk from high to low temperature has favored the condensation of solid grains, which would have later formed planets via complicated agglomeration processes. We have tried to constrain the structure of the initial disk via observationnal physical and chemical constraints regarding the solar system. These constrains focus mainly on the formation of giant planets and the observed deuterium enrichment in water. The latter depends on temperature and density profiles in the disks throughout its evolution.
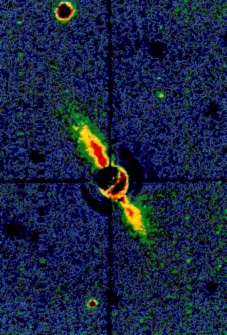
We thus have generated analytical models of an evolutionary nebula to generate these profiles, depending on three characteristic parameters: the initial disk mass and radius, and the intensity of \ turbulent transport. In order to fit observations the mass of the initial disks must have been between 0.03 and 0.3 solar masses, its radius between 8 and 28 astronomical units and the intensity of the turbulent transport must have been such that the turbulent viscosity expressed in units of the sound velocity and the disk height, must have been between 0.003 and 1.
High viscosity disks are characterized by MHD turbulence, while the low viscosity disks (turbulent viscosity between 0.003 and 0.01) are characterized by hydrodynamical turbulence. Magnetic fields in the selected nebulae are also calculated. Their lifetime is found equal to 104 years for to 10 5 years. Their strengths are consistent with that of the remanent magnetism found in carbonaceous chondrites. The deuterium enrichment in water throughout the nebula became uniform in no more than a few millions of years for lower viscosities, in less than 100,000 years for medium viscosities (0.03), still faster for higher values of the viscosity. In all cases, the uniform D/H ratio, which corresponds to a complete reprocessing of the deuterated water coming from the presolar cloud, is consistent with enrichments observed in LL3 meteorites, Uranus and Neptune. Scenarios providing us with an interpretation the high D/H ratio observed in comets are discussed. The first scenario in which comets coming from Oort cloud were formed very rapidly in the Uranus-Neptune region of the turbulent nebula and expulsed towards the Oort cloud prior to the complete formation of these planets implies some reprocessing in the nebula of the matter coming from the presolar cloud. It may not be easy however to eject comets towards the Oort cloud quite early in the history of the Solar System. It might be, according to the second scenario, that both comets coming from the Oort cloud and comets of the Jupiter family were formed farther and later than Neptune in a non turbulent region of the nebula. In such a case, comets may have kept to a large extent the chemical signature of the interstellar medium. The fact that several comets exhibit the signature of crystalline silicates which can be formed only at high temperatures expected to have occurred in the inner part of the nebula favors the first scenario. The detection of such silicates in the interstellar medium would favor the second scenario.
The intensity of the turbulent transport derived from these observations remains yet to be explained. We have proposed a consistent scenario, based on nonlinear hydrodynamical instabilities to explain it. Also, the presence of turbulence hinders the sedimentation of dust grains onto the midplane, and thus the formation of planets from dust grains via gravitational instability. To overcome this difficulty, we have proposed that turbulence generates large scale vortices which may trap of particules, and thus, locally enhance the dust grain density. This scenario has since been confirmed via several simplified numerical studies.
Scale Invariance and Scale Symmetry
The scale symmetry is a symmetry thought to occur in systems with no characteristic scale. Using a formalism inspired by the work of Nottale, we have shown that there is a deep analogy between scale symmetry and speed relativity in mechanics. This analogy is based on the analogy between equivalence of all systems of units and symmetry by translation. It leads to non-trivial practical applications when applied to random fields with statistics coupling a wide range of scales. For example, the analogy provides a systematic classification of the statistics of such scale dependent random fields, using only the fiexd points of the symmetry transformation. Also, the analogy enables to develop a unified formalism to describe the symmetry breaking occuring in statistical systems.

Rigorous scale invariance is a concept pertaining only to infinite systems. In the presence of finite size cut-offs, one can also use the same ideas to generalize the scale symmetry into a finite size scale symmetry. This new symmetry :
- includes the traditional self-similarity as a limiting case, when the cut-offs are set to infinity (infinite size-system);
- is consistent with the traditional finite size scaling approach already used in critical phenomena;
- enables the computation of some of the universal functions appearing in the finite size scaling formulation;
- allows scale transformations leaving the cut-offs invariant, like in the traditional renormalization approach;
- can be formulated to allow for positive or negative fields and parameters;
- leads to new predictions about the shape of some distributions in critical phenomena or turbulence which are in very good agreement with the experimental or numerical findings.
Turbulence and Intermittency
Scale invariance is thought to be a fundamental property of Turbulence. I have shown that it can be a source of anomalous scaling laws, via zero modes of a scale invariant operator. The understanding of the exponents characterizing these scaling laws therefore requires the taking into account of the scale symmetry. Using the formalism described above, we have shown that the possible statistics fall into different classes, depending on the codimensions of the most intermittent structures.

These classes include the exponents corresponding to a log-Poisson statistics, and those appearing in the thermo-dynamical distribution discussed by Castaing. They also admit the Kolmogorov K41 and the mono-fractal case as limiting solutions. The new scale symmetry formalism also leads to an electro-magnetic analog of turbulence, where the influence of the forcing mechanism is lumped into the analog of an electric field. The formalism was generalized to deal with coupled random fields. When applied to the case of passive scalar in turbulence, it leads to the prediction that Log-Poisson Statistics for velocity fields implies a similar type of Statistics for the passive scalar.
I have also tried to use multi-fractal theory to characterize the regularity of a given field. Wavelet methods have already been proposed to explore the regularity properties of velocity fields, and the estimation of their exponent of Holder h via the concept of multifractal analysis which provides fractal dimensions of the subspace where the singularity exponent is worth h. However, multifractal analysis is an overall statistical method that does not allow us to determine the value of the singularity exponents. provides only aggregate information on local Holder exhibitors, via their probability of occurrence. In order to explore the local regularity properties of a velocity field, we have developed a statistical algorithm, which locally estimates Holder continuity and is compatible with global multifractal analysis. We compared the results of our method… with results using inertial energy dissipation as described above. We observe that the The term dissipation does indeed become greater for velocity fields that are less regular according to our indicator. The exact spatial distribution of Holder’s local exponents, however, shows non-trivial behaviour and does not exactly match the distribution of inertial dissipation.
Furthermore, we have studied the universality of the functions of the Eulerian velocity structure using velocity fields obtained by the technique of particle image Velocimetry (PIV) in experiments and direct numerical simulations (DNS) of the Navier-Stokes equations. We have shown that the functions of the numerical and experimental structure of velocities up to order 9 follow logarithmic universality (Castaing et al. Phys. D Nonlinear Phenom. 1993); this leads to a description by a universal curve, when units including logarithmic Reynolds number dependence are used. We then examined the meaning and consequences of such a log-universality, and showed that it is related to the properties of « multifractal free energy », based on an analogy between multifractal and thermodynamics. This paper shows that in such a framework, the existence of a fluctuating dissipation scale is associated with a phase transition writing the relaminarization of the raw velocity fields with different Hlder exponents. Such a phase transition has already been observed using the functions of the Lagrange velocity structure, but was until now considered out of reach for the actual data.
Subgrid Scale Modelling
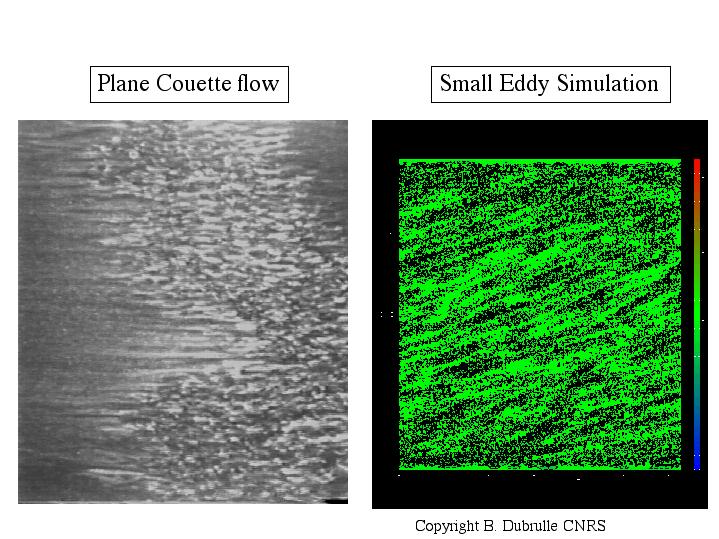
In classical turbulence theory, the closure problem arises when considering the statistical or filter average of the forced Navier-Stokes equations: the action of the unresolved scales appear via the Reynolds stresses, which need to be prescribed in order to close the system. Most turbulence models try to close the system by prescribing directly the shape of the Reynolds stresses using, e.g. dimensionnal arguments and arbitrary parameters which need to be calibrated. A famous example is the eddy-viscosity. We have used a novel approach, in which the Reynolds stresses are computed by an estimate of the r.m.s. or subgrid velocities. The estimate is done via a dynamical equation linking the average or resolved velocity and the r.m.s. or subgrid velocities. This equation is not postulated, but derived from the constitutive equations using two simplifying assumptions: i) the non-linear interactions of the small scale scales between themselves is modeled via a turbulent viscosity; ii) the small scale generation via the breaking of large scale structures into small, intermittent scales, (plumes, streaks, vortex filaments) is modeled by a random small scale forcing with a short time correlation and spatially homogeneous. This results in a linear stochastic equation for the random small scales, which can be analytically solved in the shear flow geometry by a decomposition of the small waves into localized wavepackets. These wavepackets are transported by the mean velocity and have wavenumbers and amplitude which evolve according to the mean strain and the stochastic forcing. In this model, only the non-local interactions between the small random scales and the mean large scale flow are exactly taken into account. It is thus refered to as a « non-local model » of turbulence. It is in fact a generalization of the Rapid Distorsion Theory (RDT). This new model allows both analytical predictions and numerical implementation. We present below a few applications of our modelling.
2D turbulence
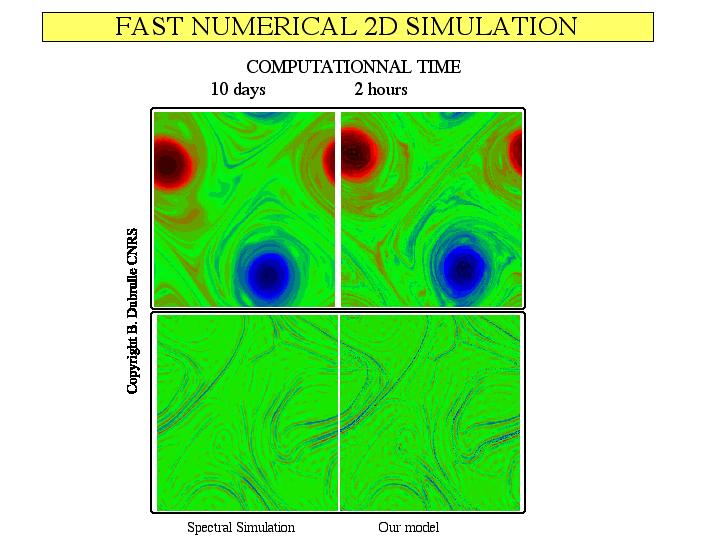
In 2D turbulence, we have shown by comparison with Direct Numerical Simulation (DNS) that the non-local approximation is excellent, due to the condensation of the large scale vortices. We have then implemented our model numerically, and studied two typical problems of 2D turbulence: decaying and forced turbulence. Our model was then compared with DNS at higher resolutions. Example of spectral comparison is given in the figure. This comparison shows that the performances of our model are better than the DNS, at the same resolution and comparable computational cost. The most significant improvement is observed in the small scale component, so that the effective inertial range increases by one or several decades compared to the DNS.
Equilibrium profiles of channel flows
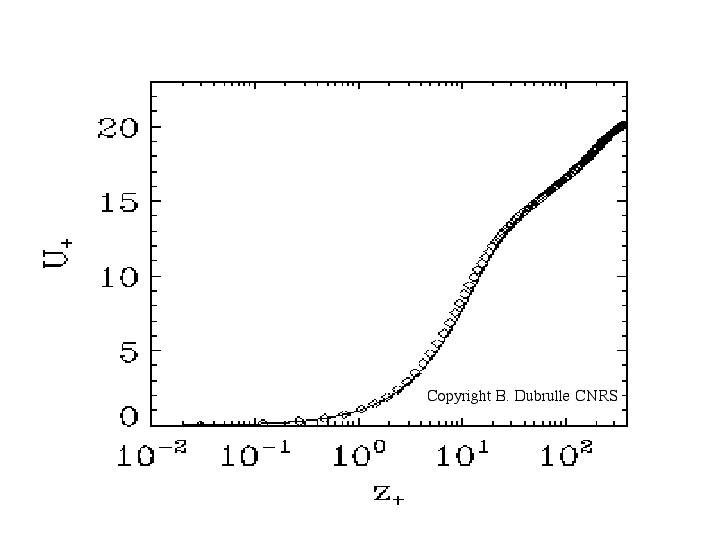
In plane parallel geometry, our model can be used to derive analytically the equilibirum profiles both in the near-wall and core regions. In the near-wall region we derive a general expression for the velocity profile which is linear in the viscous layer and logarithmic outside. This expression involves two physical parameters: the von Karman constant and the size of the viscous layer (which can be computed via a numerical implementation of our model). Fits of experimental profiles using our general formula provides reasonable values of these parameters (Karman constant between 0.4 and 0.45, size of the viscous layer about 15 wall units). In the core region, we find that the shape of the profile depends on the geometry of the flow: it ranges from algebraic in channel flow, to exponential in the bulk of boundary layers, or linear in plane Couette flow. This classification is consistent with Oberlack’s system, which is based on symmetry arguments. Fits of boundary layer flows or channel flows at different Reynolds number over the whole flow region are performed using our results, and are found to be in very good agreement with available data (see Fig).
Scaling laws in thermal convection
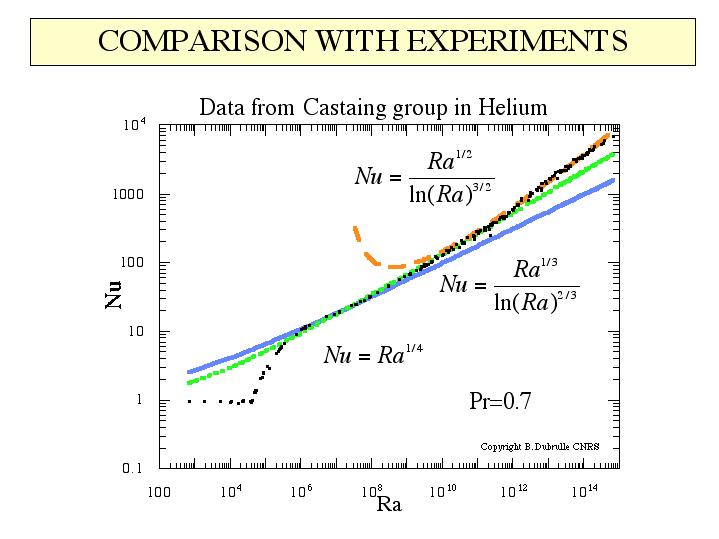
Our model can be used to predict both the structure and the scaling laws in thermal convection. In the boundary layer, the velocity profile is logarithmic and the temperature decays like the inverse of the distance to the wall. The transport of heat depends on the interplay between the thermal, viscous and integral scales of turbulence, and thus, on both the Prandtl number and the Reynolds numbers. At low Reynolds numbers, when most of the dissipation comes from the mean flow, we recover power classical scaling regimes of the Nusselt versus Rayleigh number, with exponent 1/3 or 1/4. At larger Reynolds number, velocity and temperature fluctuations become non-negligible in the dissipation. In these regimes, there is no exact power law dependence the Nusselt versus Rayleigh or Prandtl. Instead, we obtain logarithmic corrections to the classical soft (exponent 1/3) or ultra-hard (exponent 1/2) regimes, in a way consistent with the most accurate experimental measurements available nowadays. Exampls is given in the figure, showing the comparison between the data of the Castaing group in Helium, versus the theoretical predictions (lines). The theory has also been extended to describe turbulent thermal convection at large Prandtl number. We show that two regimes arise, depending on the Reynolds number Re. At low Reynolds number, Nu Pr^{-1/2} and Re are a function of Ra Pr^{-3/2}. At large Reynolds number Nu Pr^{1/3} and Re Pr are function only of Ra Pr^{2/3} (within logarithmic corrections). In practice, since $Nu$ is always close to Ra^{1/3}, this corresponds to a much weaker dependence of the heat transfer in the Prandtl number at low Reynolds number than at large Reynolds number. This difference may solve an existing controversy between measurements in SF6 (large Re) and in alcohol/water (lower Re). We link these regimes with a possible global bifurcation in the turbulent mean flow. We further show how a scaling theory could be used to describe these two regimes through a single universal function. This function presents a bimodal character for intermediate range of Reynolds number. We explain this bimodality in term of two dissipation regimes, one in which fluctuation dominate, and one in which mean flow dominates. Altogether, our results provide a six parameters fit of the curve $Nu(Ra,Pr)$ which may be used to describe all measurements at Pr >0.7.
Structure of the Planetary Surface Layer
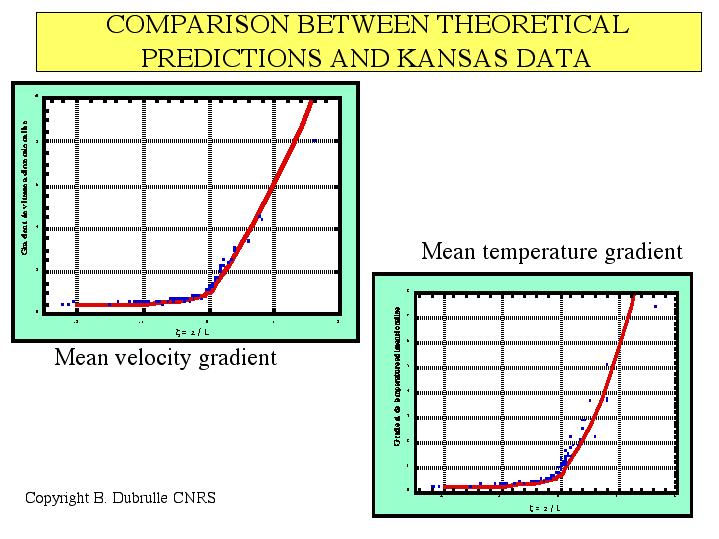
Our model was also used to determine the mean velocity and temperature in the Planetary Surface layer, as a function of the stability of the layer. Our predictions are compared with observations drawn form the Kansa 68 data. The theory allows for analytic non perturbative solutions in any surface layer and can be easily generalized to include other effects, such as rotation, and thus could potentially be used to estimate momentum and temperature fluxes in the planetary boundary layer for larger-scale (climate) models.
2D MHD with a background shear
Turbulent transport and equilibrium profile are studied in 2D MHD in the presence of a background shear flow and a large–scale magnetic field; the latter are assumed to point in the same direction and to vary in the perpendicular direction. We explore both kinematic and dynamic cases in the case of unit magnetic Prandtl number and calculate the magnetic vector potential and momentum fluxes (due to total Reynolds stress), thereby determining turbulent diffusivity and viscosity and equilibrium profile of the mean shear flow. The turbulent diffusion is found to be suppressed for a strong (large–scale) magnetic field. The Lorentz force changes the sign of the total Reynolds stress resulting in the turbulent viscosity with an opposite sign compared to that in the hydrodynamical case; the former reduces the amplitude of the total Reynolds for a fixed shear. Since the divergence of momentum flux acts as an effective force on the background shear, the presence of the magnetic field can lead to an equilibrium shear profile which is different from that of the pure hydrodynamic case.
Turbulence and Dynamo
The dynamo effect is a process of magnetic field generation through the movement of an electrically conducting medium. The instability results from a competition between amplification of a seed magnetic field via stretching and folding, and magnetic field damping through diffusion. In a laminar fluid, it is controlled by a dimensionless number, the magnetic Reynolds number, which must exceed some critical value for the instability to operate. In a turbulent medium, velocity fluctuations induce fluctuations of the control parameter, making the turbulent dynamo problem similar to an instability in the presence of multiplicative noise. This so-called turbulent dynamo problem remains challenging, experimentally and theoretically. In this field, the prevailing theory is the Mean-Field Dynamo where the dynamo effect is monitored by the mean magnetic field.

In recent years, it has been shown on stochastic oscillators that this type of approach could be misleading. We have developed a stochastic description of the turbulent dynamo effect which enables us to define unambiguously a threshold for the dynamo effect, namely by globally analyzing the probability density function of the magnetic field instead of a given moment. We have also studied dynamo generation using numerical simulations in a Taylor-Green flow. Such a flow is subject to hydrodynamic bifurcations occur in between different metastable states with different dynamo action, and are triggered by the numerical noise.
The various states encountered range from stationary to chaotic or turbulent through possible oscillatory states. The corresponding sequence of bifurcations is reminiscent of the sequence obtained in the von Karman flow. We then use kinematic simulations to compute the dynamo thresholds of the different metastable states. A more detailed study of the turbulent state reveals the existence of two windows of dynamo action. Stochastic numerical simulations are then used to mimic the influence of turbulence on the dynamo threshold of the turbulent state. We show that the dynamo threshold is increased (resp. decreased) by the presence of large scale (resp. small scale) turbulent velocity fluctuations. Finally, direct numerical simulations of the magneto-hydrodynamic equations are used to explore the linear and non-linear stage of the dynamo instability.
In the linear stage, we show that the magnetic field favors the bifurcation from the basic state directly towards the turbulent or chaotic stable state. The magnetic field can also temporarily stabilize a metastable state, resulting in cycles of dynamo action, with different Lyapunov exponents. The critical magnetic Reynolds number for dynamo action is found to increase strongly with the Reynolds number. Finally, we provide a preliminary study of the saturation regime above the dynamo threshold.
At large magnetic Prandtl number, we have observed two main types of saturations, in agreement with the analytical prediction described above :
- intermittent dynamo, with vanishing most probable value of the magnetic energy ;
- dynamo with non vanishing mean value of the magnetic energy.
We describe a sequence of bifurcation of the dynamo at low Reynolds number and at increasing magnetic Prandtl number, where the dynamo switches from stationary mode to chaotic modes in a complex manner, involving intermittency in a way reminiscent to what is observed in dynamical systems with low number of degrees of freedom. We also find that the bifurcation is subcritical, and show its bifurcation diagram. We connect the associated hysteretic behavior with hydrodynamics changes induced by the Lorentz force. We show the geometry of the dynamo magnetic fields and discuss how the dynamo transition can be induced when an external field is applied to the flow. Finally, I am member of the VKS collaboration, that experimentally study dynamo action.
Statistical Mechanics of Out of Equilibrium Systems
Turbulence is a very special example of far from equilibrium system. Describing the complexity of turbulent flows with tools from statistical mechanics is a long-standing dream of theoreticians. In 1949, five years after the publication of its solution for the problem of phase transition in the 2D Ising model, Onsager published a notorious study of the statistical mechanics of the point vortex model , a special solution of the 2D Euler equations that allows to interpret the emergence of long lived coherent structures in terms of the pairing between vortices mutually interacting through a long range Coulombian potential.
That Onsager chose the special case of 2D turbulence is probably not a coincidence: as soon as 1947, he was aware of the existence of the dissipative anomaly in 3D flows that precludes the use of classical equilibrium tools such as micro-canonical measures. In other words, the non-vanishment of the energy flux at vanishing viscosity for 3D flows makes 3D turbulence an intrinsically far-from-equilibrium system, which cannot be approximated by crudely setting the viscosity to zero in the Navier-Stokes equations. Quite remarkably, the dissipative anomaly does not exist in 2D, justifying Onsager’s choice for his statistical mechanics approach. Since Onsager, the description of 2D turbulence using statistical mechanics has greatly improved. Starting from the seminal work of Robert-Miller-Sommeria and subsequent work from then, it led to a description of the coherent structures that seems to match the observed large scale organization in experimental and numerical 2D turbulence. However, the 3D case still escapes theoretical grasp.
A first light of hope may come from the special case of von Karman (VK) turbulence, a now classical human size experiment that reaches very large Reynolds numbers of the order of $10^6$ through the stirring of a fluid in between two counter-rotating propellers. At this value, there is no doubt that the turbulence is fully developed with a wide range of interacting scales. Previous analysis of turbulence properties in the middle shear layer evidenced scaling properties and intermittency corrections in agreement with other measurements in fully developed turbulent flows in different geometries. Some indications exist though, that the number of effective degrees of freedom in a turbulent VK flow is not so large : at Reynolds number around $10^5-10^6$, one can perform Poincare maps of the torque exerted by the turbulence on each propeller and exhibit beautiful attractors, limit cycles, or any kind of zoology that was usually observed in dynamical systems, with only 3 or 4 degrees of freedom. This suggests that only a few global quantities would be able to describe the system so that some kind of statistical mechanics approach should be used in this system, in order to identify hydrodynamical analogues for « temperatures » or « chemical potentials ». The purpose our work is to provide experimental evidence that the large scale coherent average states observed in VK experiments can indeed be described using the language and tools from statistical mechanics.
The starting point of our analysis is the observation that VK turbulence is not isotropic. Besides, and as far as the average flow is concerned, the swirling flows obtained in VK devices seem to provide an example of 3D turbulence with axial symmetry.
We have shown that axially symmetric turbulence is an intermediate case between 2D and 3D turbulence, for which equilibrium theories yield non trivial insights. VK turbulence is however not axially symmetric, and the question remains open whether the predictions obtained using an « axi-symmetric ansatz » are relevant to account for the coarse-grained properties of such flows. Preliminary comparisons performed at large Reynolds numbers suggest that the steady states of experimental VK flows can be described in terms of a restricted set of meta-stable equilibria of the 3D axially symmetric Euler equation. I have shown how the light of the statistical mechanics can be used beyond the scope of ideal theories, to provide a useful framework of analysis of the data. We will evidence a deep analogy between the VK steady states and lattice models of Ferro-magnetism. We call this analogy « Ferro-Turbulence ».
We have developped a theory and used measurements performed in a turbulent von Karman flow to show that there is actually a direct link between its fluctuations and the mean flow properties, in a way analogous to the classical Fluctuation Dissipation Theorem. This link provides a measurement of effective statistical temperatures, that are found different according to the observable. The theory might be generalizable to other out of equilibrium systems, such as granular flows. The simplified thermodynamic approach of the incompressible axisymmetric Euler equations we are using is based on the conservation of helicity, angular momentum and microscopic energy. Statistical equilibrium states are obtained by maximizing the Boltzmann entropy under these sole constraints. We assume that these constraints are selected by the properties of forcing and dissipation. The fluctuations are found to be Gaussian while the mean flow is in a Beltrami state. Furthermore, we show that the maximization of entropy at fixed helicity, angular momentum and microscopic energy is equivalent to the minimization of macroscopic energy at fixed helicity and angular momentum. This provides a justification of this selective decay principle from statistical mechanics. These theoretical predictions are in good agreement with experiments of a von Karman turbulent flow and provide a way to measure the temperature of turbulence and check Fluctuation-Dissipation Relations (FDR). Relaxation equations are derived that could provide an effective description of the dynamics towards the Beltrami state and the progressive emergence of a Gaussian distribution. They can also provide a numerical algorithm to determine maximum entropy states or minimum energy states.
We have also characterized the thermodynamical equilibrium states of axisymmetric Euler-Beltrami flows. They have the form of coherent structures presenting one or several cells. We find the relevant control parameters and derive the corresponding equations of state. We prove the coexistence of several equilibrium states for a given value of the control parameter like in 2D turbulence [Chavanis and Sommeria, J. Fluid Mech. 314, 267 (1996)]. We explore the stability of these equilibrium states and show that all states are saddle points of entropy and can, in principle, be destabilized by a perturbation with a larger wavenumber, resulting in a structure at the smallest available scale. This mechanism is therefore reminiscent of the 3D Richardson energy cascade towards smaller and smaller scales. Therefore, our system is truly intermediate between 2D turbulence (coherent structures) and 3D turbulence (energy cascade). We further explore numerically the robustness of the equilibrium states with respect to random perturbations using a relaxation algorithm in both canonical and microcanonical ensembles. We show that saddle points of entropy can be very robust and therefore play a role in the dynamics. We evidence differences in the robustness of the solutions in the canonical and microcanonical ensembles. A scenario of bifurcation between two different equilibria (with one or two cells) is proposed and discussed in connection with a recent observation of a turbulent bifurcation in a von Karman experiment [Ravelet et al., Phys. Rev. Lett. 93, 164501 (2004)].
Quantum Turbulence
At low temperatures, liquid Helium 4 is subject to a phase transition, from a classical fluid phase HeI (T> 2.18 K at saturated vapor pressure) to a superfluid one HeII which behaves like a two-fluid system, with one normal component, following classical Navier-Stokes equations, and one superfluid irrotational component, with quantized small scale vortices and zero viscosity. Both components interact with these vortices, which gives raise to the mutual friction between these components. When a superfluid Helium 4 flow is forced within a tank or past an obstacle, it can become turbulent. An important open question is how much analogy such « quantum turbulence » bears with « classical » turbulence, and how much it can be explained within the above mentioned two-fluid model, and its mutual friction term . I am member of the SHREK (Superfluid Helium high REynold number von Karman flow) collaboration that experimentally study dynamo quantum turbulence.

The SHREK facility exploits the capacities of a high cooling power refrigerator (400W at 1.8K) for a large dimension von K�rm�n flow (inner diameter 0.78 m), which can work with gaseous or subcooled liquid (HeI or He-II) from room temperature down to 1.6 K. The flow is produced between two counter-rotating or co-rotating disks. The large size of the experiment allows exploration of ultra high Reynolds numbers based on dissipative scale and rms velocity1 (R?>10000) or resolution of the dissipative scale for lower Re. We have measured the dissipation in SHREK experiment for different forcing conditions, through a regime of global hysteretic bifurcation. Our macroscopical measurements indicate no noticeable difference between the classical fluid and the superfluid regimes, thereby providing evidence of the same dissipative anomaly and response to asymmetry in fluid and superfluid regime. A detailed study of the variations of the hysteretic cycle with Reynolds number supports the idea that (i) the stability of the bifurcated states of classical turbulence in this closed flow is partly governed by the dissipative scales and (ii) the normal and the superfluid component at these temperatures (1.6K) are locked down to the dissipative length scale.
Statistical Mechanics and Climate
While the alternation of glacial and interglacial periods, on a scale of tens of thousands of years, is linked (still somewhat mysteriously) to variations in the Earth’s orbital parameters, there are also much more rapid climate changes, the cause of which remains largely unknown. Indeed, the climate of the last ice age, particularly around the regions bordering the North Atlantic, was marked by very significant warming and cooling, of the order of 10 C or more, in just a few decades. These abrupt variations are most certainly linked to changes in the ocean circulation in the Atlantic. This continues to give rise to many concerns about the future of this ocean circulation in the current context of climate change. Indeed, some models predict a bistable behaviour of this circulation, which would explain repeated shifts during the ice age, in the presence of external forcing, in the form of recurrent freshwater inputs from ice caps. While this idea helps to explain some aspects of the phenomenon (bistability, abrupt changes, etc.), other characteristics (pseudo-periodicity, global nature of the events, independence with respect to the size of the ice caps, etc.) do not easily fit into this classical scheme. We explored an alternative hypothesis, based on self-sustained oscillations of the thermohaline circulation.
Such oscillations have recently been observed in turbulent flows, notably at the SPEC. They can result a priori from two scenarios: either via a linear oscillating mode of the system, or via a stochastic resonance between two equilibrium states of the system. During this thesis, we studied the relevance of these two scenarios, by coupling analytical calculations and simulations using an existing numerical model, commonly used by climatologists (CLIMBER). In particular, we sought to characterize the equilibrium states of the system and their associated relaxation equations using a new formalism of out-of-equilibrium statistical mechanics, developed by Robert and Sommeria for two-dimensional turbulence, which makes it possible to obtain the organization of the fluid on a large scale by a principle of maximization of an entropy under constraints. The equilibrium structures obtained reproduce well the zoology of the vortices obtained in two-dimensional turbulence. The formalism also makes it possible to understand and reproduce the different bifurcations between the equilibrium states obtained, by varying the control parameters. This very general theory in its formulation can also be extended to the case of a two-dimensional ocean, subjected to temperature and salinity variations, and could thus allow to initiate a statistical mechanics of thermohaline oscillations.
Maximum Entropy Principle (MEP) and Climate
In 1976, Paltridge show that the temperature distribution at the Earth’s surface could be reproduced fairly accurately, using an empirical principle of maximizing entropy production. This result had aroused a lot of interest at the time, particularly because it opened up the prospect of building climate models without adjustable parameters, which were not very demanding in terms of digital resources. However, the empirical nature of the maximization principle, as well as some mysteries surrounding the parameterization of clouds had led the community to suspect that this beautiful result was only due to a nefarious adjustment of well-chosen constants, and the Paltridge model had fallen into oblivion.
With D. Paillard, we supervised a PhD student, Corentin Herbert to take the model in detail, to clean it of all its arbitrariness, in order to make it a true model without adjustable parameters, which could be scientifically compared with results from observations or climate model simulations. To do this, Corentin completely redesigned the model, introduced a modern radiative transfer module and reconstructed it in such a way that other effects, such as the water cycle or the CO2 cycle, could be included. This work allowed the construction of a new climate model that is flexible, fast, and without adjustable parameters Although this model is beginning to interest the climate community, it is still based on an empirical principle without theoretical foundations.
To understand this mystery, Didier and I hired a new PhD Martin Mihelich . During his thesis, Martin worked on off-equilibrium model systems (ASEP, zero-range) to study the validity of the principle of entropy maximization in an analytical and numerical way. He first showed that the principle of maximum entropy production was in fact a min-max (one first minimizes the entropy production to find all possible stationary systems, then one selects the one with the highest entropy production to keep the most stable). He also highlighted the link between the entropy production maxima and the entropy maxima. of Kolmogorov-Sinai , then between the maxima of the Kolmogorov-Sinai entropy, and the minimum mixing-time. From all this, we have concluded that if the principle of maximum entropy production works, it is because it selects the states with the weakest mixing time, that is, those that converge most rapidly to the stationary state. Since the first principle is easier to implement than the second, this justifies its practical use in complex systems, such as climate models. Our next PhD Vincent Labarre has applied and principle in convection.
Looking for singularities of the Navier-Stokes Equations
In nature, many phenomena involve the movement of viscous fluids, which can be written by the fundamental equations of Navier-Stokes (NS). These partial differential equations translate the conservation laws of mass, momentum and energy. They form the basis for numerical simulations of fluid dynamics in fields as varied as aeronautics, astrophysics and climate studies. The economic stakes associated with these studies are also considerable, since the energy losses induced by the effects of turbulence (land, sea and air transport, sources of wind and hydropower) are considerable.
A central issue, common to all these areas, is to correctly describe the dissipation of energy during the flow of a fluid. Under the action of external forces, the fluid becomes turbulent, and is structured in swirling motions over a range of orders of magnitude. The mechanical energy at the origin of the global motion is thus transferred to smaller and smaller structures, only to be dissipated under the effect of viscosity, at the smallest scales, for which the Reynolds number Re is typically of the order of 1 (Kolmogorov scale). In order to simulate numerically the behaviour of fluids and this energy conversion, it is crucial to know whether the Navier-Stokes equations are correct: does a solution obtained at a time T remain regular or, on the contrary, does it develop singularities after a finite time? The answer to this question is for the moment an open-ended problem, so much so that the proof of the existence of globally regular NS solutions in dimension 3 has been identified as one of the seven millennium challenges by the Clay Mathematics Institute (CMI), each with a prize of 1 million dollars.
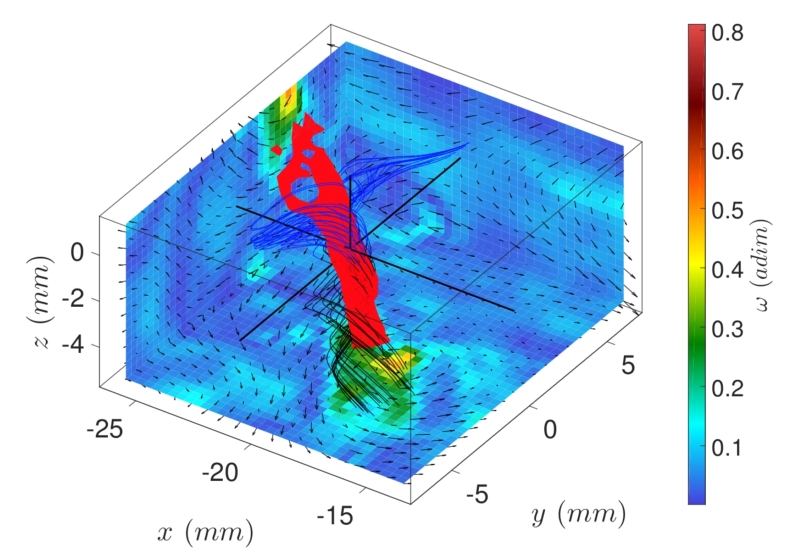
One of the indirect proofs of the existence of singularities in NS could come from the behavior of the energy dissipation rate when the Reynolds number becomes very large. Since Taylor « s experiments (1934), it has been known that this quantity is saturated and becomes independent of viscosity within the limit of low viscosity? (i.e. for large Reynolds numbers). As early as 1940, Lars Onsager proposed to link this observation to the existence of singularities of velocity, which would produce an « inertial » dissipation, independent of viscosity. It was only in 2000 that two French mathematicians, Jean Duchon and Raoul Robert, succeeded in calculating the expression of this inertial dissipation, using the formalism developed in 1934 by Jean Leray. The experimental measurement of this inertial dissipation in a turbulent flow encountered technical difficulties for a long time, due to the difficulty of measuring the velocity field over a sufficiently wide range of scales and positions. The recent development of methods for measuring fluid velocity fields by means of a series of dispersed particle velocity fields on scales ranging from the ecimetre to the millimetre and covering the frequency range 1Hz – 1kHz now makes it possible to overcome this difficulty.
Using this technique, my team has just carried out the first quantitative experimental measurement of inertial dissipation in a turbulent vortex flow [134]. The measurements show for the first time, the emergence of extreme inertial dissipation events at scales where viscosity is supposed to dampen all motion and dissipate all energy. The velocity fields corresponding to these extreme events have been classified according to their topological nature. Four classes of velocity fields have been observed, ranging from fronts, spirals, to jets, to cusps, to spirals. These structures could correspond to pre-singularities, events that are precursors to the singularities sought by mathematicians. We subsequently showed that they were responsible for the intermittent turbulence and that their behavior was consistent with multifractal theory. These observations underscore the non-trivial nature of the movements and energy transfers at the dissipative scales, and place strong constraints on the size of the scales to be solved in order to hopefully simulate real fluids accurately. To go one step further, we obtained ANR funding over 4 years (EXPLOIT project), for the construction of a giant (1 m in diameter!) von Karman experiment allowing easier access to dissipative scales and 3D measurements.




