Ondes et tourbillons dans la matière active sous-critique : un nouveau modèle

La matière active est composée d'entités individuelles convertissant de l'énergie en travail, ce qui entraine leur mise en mouvement, et leur permet de s'organiser spontanément du fait de leurs interactions mutuelles. De nombreux systèmes vivants peuvent être vus sous cet angle, mais aussi, de plus en plus, des ensembles de microparticules actives synthétiques ou extraites de cellules. L’approche théorique de la matière active ne bénéficie pas des résultats généraux valides à l’équilibre thermodynamique, mais elle en garde les thèmes principaux : symétries, lois de conservation, et transitions de phase sont déterminantes, mais les propriétés émergentes de la matière active sont bien souvent nouvelles, offrant de nouvelles voies d’auto-organisation dynamique.

Dans un article récent publié dans PNAS, Hugues Chaté (IRAMIS/SPEC), Xia-qing Shi et le groupe de Tian Hui Zhang (Université de Suzhou) montrent qu'un système de colloïdes actifs juste sous critique (i.e. près du seuil de leur mise en mouvement) présente de nouveaux types de dynamique collective auto-organisée spectaculaires, comme des tourbillons auto-organisés isolés composés de milliers de particules.

Les systèmes de matière active généralement étudiés sont constitués d’objets (biofilaments, cellules, particules colloïdales, robots, animaux, etc…) qui bougent, même lorsqu'ils sont seuls ou isolés. Leurs propriétés collectives sont fascinantes et leur étude permet de mieux comprendre comment l'énergie injectée dans le système est convertie en travail.

Les résultats des études réalisées par Hugues Chaté (IRAMIS/SPEC) et Xia-qing Shi, associés au groupe de Tian Hui Zhang (Soochow University) et récemment publiés dans PNAS, montrent que des particules isolées potentiellement actives mais pratiquement sans mouvement perceptible peuvent présenter des propriétés d'organisation collective spécifiques et remarquables du fait de l'interaction avec leur congénères. En combinant expériences, théorie et simulations numériques, il est montré qu'une telle matière active sous-critique peut être réalisée avec des « rouleurs de Quincke » : par ses travaux pionniers (1896) Georg Hermann Quincke* a montré que des particules colloïdales isolantes immergées dans un fluide conducteur et soumises à un champ électrique continu d'intensité supérieure à un seuil E_c subissent une instabilité conduisant à leur rotation dans le fluide. Pour des particules plus denses que le fluide, les particules commencent à rouler au fond du récipient dans une direction arbitraire.

Cette dynamique collective des rouleaux de Quincke* a déjà été étudiée dans le régime supercritique E > E_c. Il est ici montré que des phénomènes collectifs spectaculaires émergent aussi en régime sous-critique, i.e. pour un champ inférieur à E_c. Dans ce régime une certaine dynamique est possible, parce que les particules proches les unes des autres peuvent commencer à rouler même pour E < E_c. Les phénomènes organisés rapportés, fonction de la densité Φ de particules, incluent des ondes d'activité rapides et des tourbillons isolés stables de taille arbitraire composés de milliers de particules se déplaçant à la même vitesse.

Résultats expérimentaux : (A) Schéma du dispositif expérimental. (B-J) Différentes vues où les particules sont colorées selon leur vitesse (selon le code couleur mentionné à droite). L'échelle spatiale mentionnée est de 100 μm. Les particules au repos sont laissées en blanc. Les figures de la rangée supérieure présentent une densité de particules élevée (B-E, Φ ≃ 0.4 ) et sont ordonnées de gauche à droite par valeur croissante de E/Ec. De même pour la rangée inférieure où la densité de particules est faible (F-J, Φ ≃ 0.2).

Différentes configurations sont obtenues selon les valeurs de E/E_c : les images B et F montrent des clusters au repos, avec un ordre hexatique local de 0,65 E_c. (C) large vague d'activité à E = 0.89 E_c. (D) flocage sous-critique à grande échelle à E = 0.98 E_c. (E) Flocage sous-critique à E = 0.98 E_c. (G) Activité localisée à E = 0.9 E_c. (H) Tourbillon autostable isolé à E = 0.948 E_c. (I) Anneau autostable isolé à E = 0.968 E_c. (J) Flocon en spirale à E = 0.98 E_c.

Ces dynamiques collectives remarquables ne peuvent être expliquées par les modèles simples usuellement applicables à de tels systèmes. Un nouveau type de modèle doit être introduit pour rendre compte de l'ensemble des phénomènes observés.

Résultats de la modélisation : (A-E) Configurations typiques dans un domaine de 960 μm avec des conditions aux limites périodiques. Les disques de diamètre 10 μm sont centrés sur les positions des particules. Les particules immobiles sont en blanc tandis que celles en mouvement sont colorées selon leur vitesse avec le code couleurs mentionné en (E). Le système est caractérisé par 2 quantités : un seuil d'activité m_c, fonction pondérée du nombre moyen de particules actives et immobiles autour d'une particlue donnée et un facteur de remplissage Φ. (A) ondes d'activité se propageant de gauche à droite dans un système dense (m_c = 8.9, Φ = 0.33, soit ~ 3900 particules). (B) régime de flocage sous-critique dans un système dense avec des particules (~ 5530) se déplaçant principalement de droite à gauche (m_c = 3, Φ = 0,47). (C-E) formation de vortex et de structure en anneau (Φ = 0.12, 1433 particules). (C) vue instantanée en régime transitoire (m_c = 3). (D) vortex final comprenant la plupart des particules du système (m_c = 0.5). (E) Configuration finale de l'anneau comprenant la plupart des particules du système (m_c = 0,05).

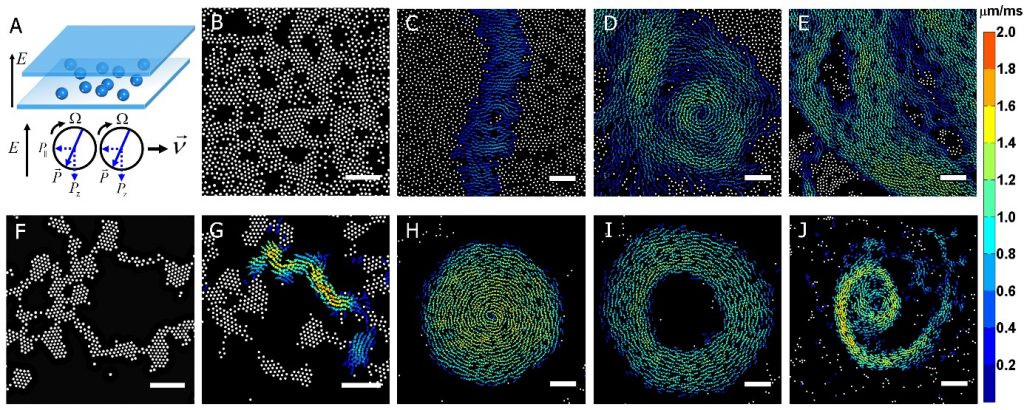
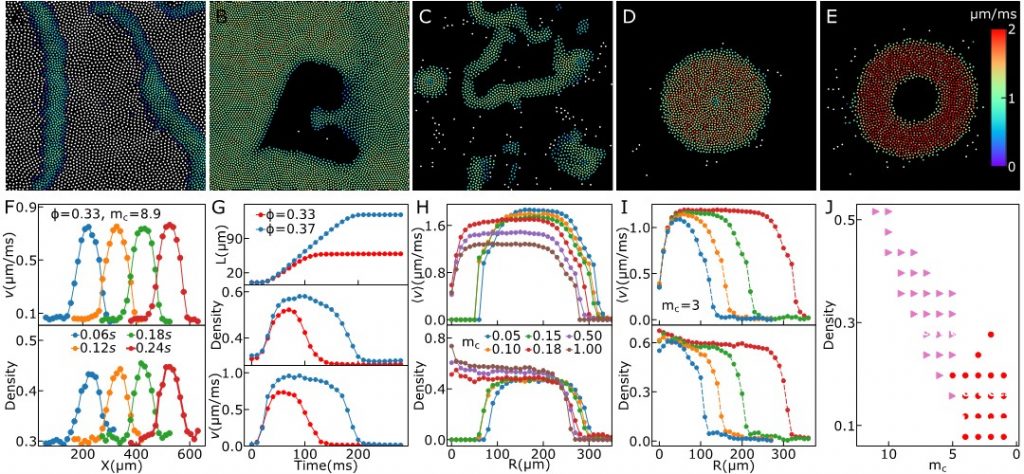
Les figures montrant les résultats expérimentaux et ceux de la modélisation L'expérience et la modélisation montrent ainsi toute la richesse du système étudié, où pour obtenir une description les propriétés collectives des particules actives considérées, il est nécessaire, au-delà des interactions entre particules usuellement considérées dans les modèles simples de matière active, de tenir compte du fluide qui les entoure et des configurations locales.

Cette étude se poursuit actuellement par l'exploration expérimentale et numérique de plusieurs pistes prometteuses : application d’un champ périodiquement modulé, utilisation simultanée de plusieurs tailles de particules, etc. Ceci permet de faire varier plus d’un paramètre que la simple valeur de champ électrique constant, révélant toujours plus de modes d’auto-organisation dynamique.

Références :

« Activity waves and freestanding vortices in populations of subcritical Quincke rollers”
Zeng Tao Liu, Yan Shi, Yongfeng Zhao, Hugues Chaté, Xia-qing Shi, and Tian Hui Zhang, PNAS 118(40) (2021) e2104724118.

*Rouleaux de Quincke : structures observées par Georg Hermann Quincke en 1896, frère de Heinrich Quincke, premier à décrire en 1882 l'angiœdème, ou œdème de Quincke.

Contact CEA-IRAMIS : Hugues Chaté (SPEC/SPHYNX)

Collaboration :

Z.T. Liu, Y. Shi, Y. Zhao, H. Chaté, X.-q. Shi, and T.H. Zhang, Center for Soft Condensed Matter Physics and Interdisciplinary Research, Soochow University, Suzhou 215006, China.