En information quantique, il est essentiel de connaître complètement l’état quantique de l’objet (photon, électron ou spin) qui porte l’information. Ceci est possible par une procédure, appelée tomographie, qui consiste à mesurer la fonction d’onde par tranches successives. La tomographie est une procédure aujourd’hui bien connue pour un photon. Elle consiste à mélanger celui-ci avec le faisceau intense d’un laser (i.e. un champ intense de photons) et à observer les interférences qui en résultent. Cette méthode ne peut s’appliquer à un fermion, car il n’existe pas l’équivalent du champ intense de photons (l’amplitude d’un champ quantique de fermion est limitée, chaque état accessible étant occupé au plus par un seul fermion). La tomographie d’un électron unique itinérant dans un conducteur demande ainsi le développement d’une méthode originale.
Les chercheurs du SPEC au CEA Saclay, en collaboration avec le LPN CNRS pour les échantillons fournis, ont réussi à atteindre la sensibilité de mesure ultime permettant la première tomographie d’un électron [1]. Pour tester cette mesure, les électrons à tomographier ont été générés sous forme de « lévitons » [2] dont la fonction d’onde bien comprise a pu être comparée aux mesures de bruit en courant révélant l’interférence de lévitons avec un champ de fermion obtenu par un petit courant électronique alternatif appliqué au conducteur. Ces résultats ouvrent la voie à la caractérisation d’états quantiques plus complexes et sont une avancée importante pour des « qubits volants », support d’information quantique, portés par des électrons dans des conducteurs quantiques.

L’objectif de notre étude a été d’effectuer la première tomographie quantique d’un fermion. Pour ceci, il a été choisi de tester une méthode proposée théoriquement récemment [3] s’appliquant à des électrons itinérants dans des conducteurs balistiques.
Mais à quoi sert la tomographie quantique? La connaissance complète de la fonction d’onde d’un fermion demanderait de mesurer parfaitement sa dépendance en temps et en énergie. Mais le principe d’Heisenberg interdit de mesurer simultanément ces grandeurs conjuguées : il faut donc un grand nombre de mesures différentes sur des systèmes strictement identiques pour explorer complètement cette fonction d’onde, ce que fait la tomographie quantique. À noter que diverses représentation de la fonction d’onde du système peuvent être utilisées : la représentation sous forme de paquet d’onde est la plus commune, mais il est aussi possible d’utiliser la « matrice densité » dont chaque élément donne la projection croisée de l’état quantique sur les éléments de la base des états choisie. Enfin, une représentation dans l’espace des phases (temps-énergie) sous la forme d’une densité de probabilité non conventionnelle (car normalement interdite) appelée « fonction de Wigner », peut aussi être utilisée. Un intérêt de cette représentation est que les valeurs négatives de la densité de probabilité attestent du caractère quantique de l’état observé.
La démonstration récente par notre équipe de la possibilité d’injecter, de façon reproductible et contrôlée, un électron unique dans un conducteur sous la forme d’une excitation électronique minimale appelée « léviton » [2], offre un système de choix pour réaliser cette première tomographie. Parmi les diverses méthodes mises au point depuis moins d’une décennie pour injecter à la demande des électrons uniques dans un conducteur. L’injection de « léviton » apparait comme la plus simple et la plus performante. Plus simple, car les méthodes précédentes utilisent des boîtes quantiques nécessitant une étape délicate de nanolithographie, tandis que celle-ci utilise un pulse de tension injectant une charge élémentaire dans le conducteur. Plus performante aussi car, pour un pulse de forme particulière (lorentzien), la charge est injectée sous forme d’une excitation électronique minimale.
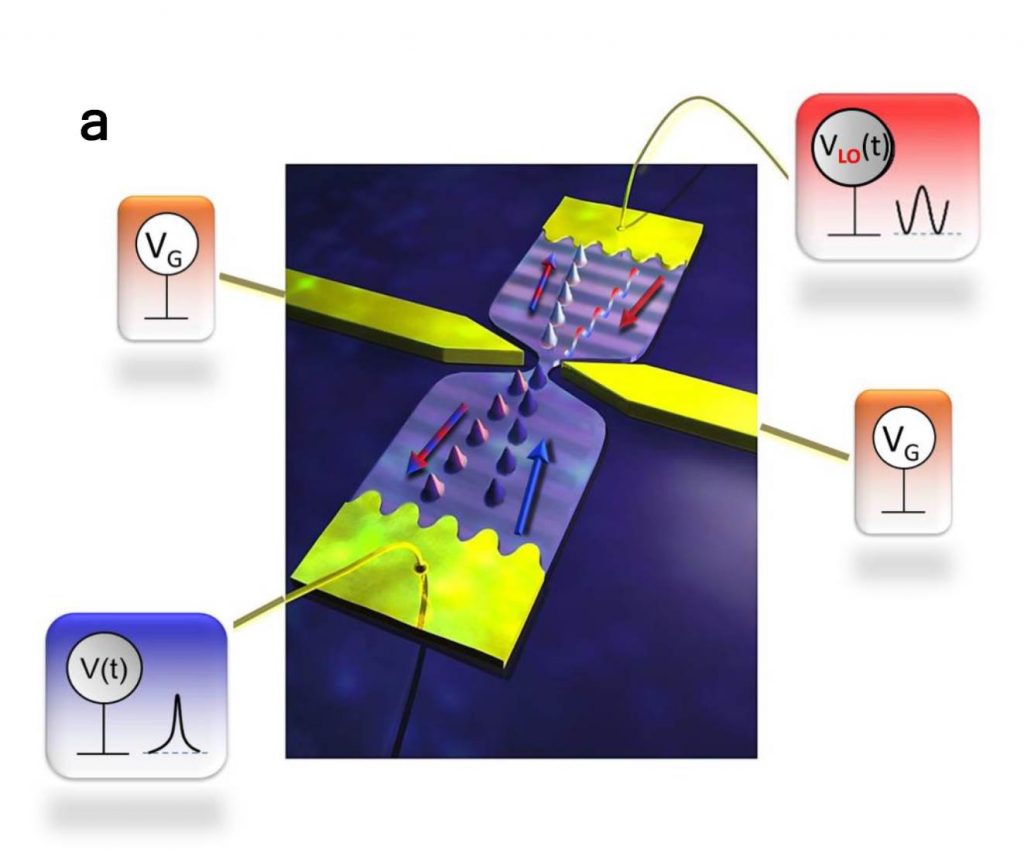
En pratique la détermination de la matrice densité en énergie de la fonction d’onde est utilisée. Ses éléments diagonaux ne sont autres que la densité de probabilité en énergie. Les termes non-diagonaux caractérisent la cohérence quantique. Leur mesure demande de trouver un moyen de faire interférer la fonction d’onde avec elle-même pour deux énergies différentes. C’est possible en envoyant les lévitons sur l’équivalent électronique d’une lame séparatrice en optique : un contact ponctuel quantique. Cette constriction ultime (voir figure ci-contre) permet une transmission partielle les lévitons dont le caractère probabiliste est révélé par des mesures de bruit. Pour sonder la distribution en énergie du léviton, on injecte des électrons cohérents avec le léviton sur le contact opposé dont on fait varier l’énergie de Fermi (i. e le potentiel électrique). Sachant que les électrons injectés par ce contact suppriment la contribution au bruit du léviton correspondant à leur énergie, le bruit à basse fréquence du courant électronique est mesuré. Pour obtenir les éléments non-diagonaux de la matrice densité, on superpose à la polarisation continue du contact une petite tension alternative de fréquence ν portant les électrons injectés dans une superposition d’état à deux énergies séparées par hν. La variation du bruit observé (avec ou sans injection d’électrons) permet de mesurer la partie diagonale de la matrice densité. Pour chaque fréquence une tranche (tomographie) hors diagonale de la matrice densité du léviton est obtenue, puis la distribution de Wigner est reconstituée (figure ci-dessous).
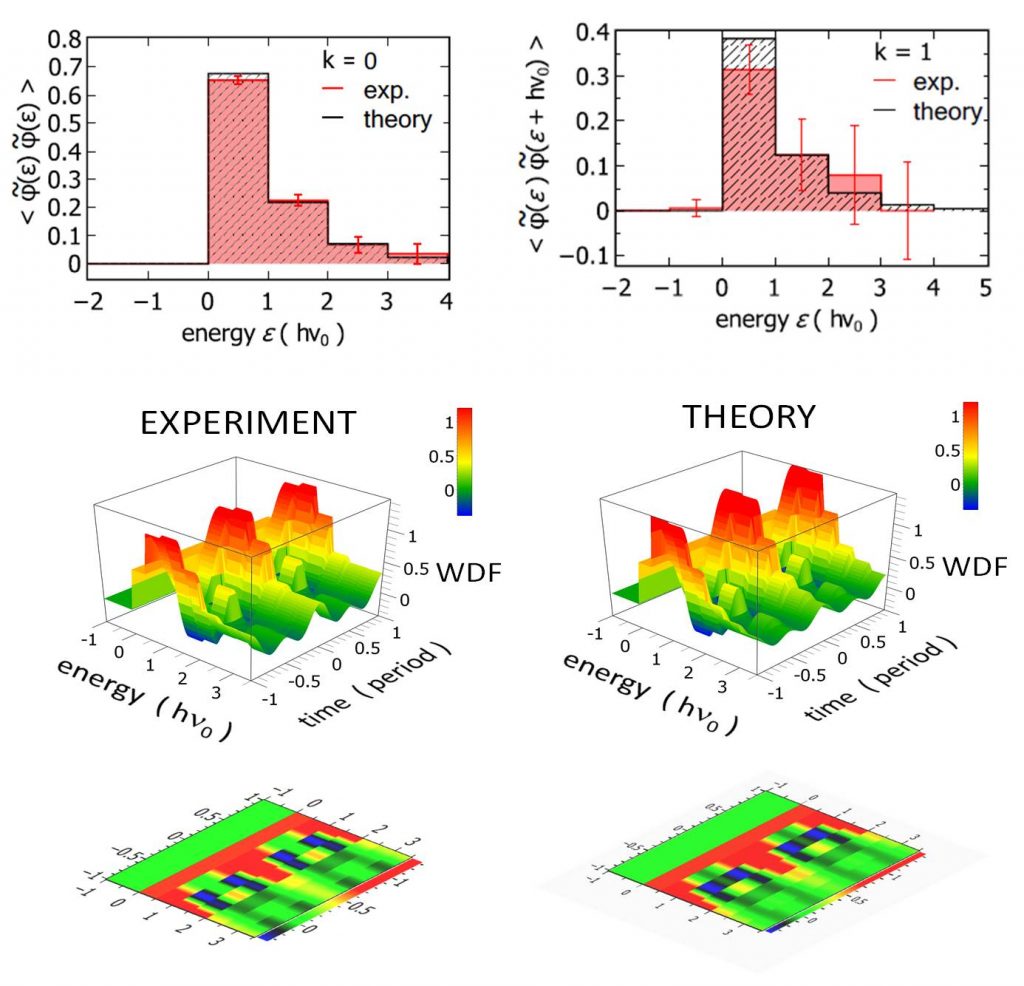
En haut : histogrammes donnant les éléments diagonaux (k=0, à gauche) et non diagonaux (k=1, à droite) de la matrice densité, d’où est déduite la fonction de Wigner expérimentale (figure 3d couleur) qui se compare bien à la fonction théoriquement prévue pour un léviton. Figure du bas : projections dans le plan temps-énergie des fonctions de Wigner expérimentale et théorique. Les zones bleues indiquent les zones dont la densité de à probabilité est négative, preuve du caractère intrinsèquement quantique de la fonction d’onde ainsi mesurée.
Cette première démonstration de tomographie quantique pour un système de fermions place les conducteurs balistiques comme une plateforme de choix, pour le développement du traitement de l’information quantique par optique quantique électronique. La méthode développée peut trouver une application directe pour sonder l’intrication de qubits électronique volants, la décohérence des électrons et leurs interactions mutuelles. Elle pourrait être également transposée aux systèmes d’atomes froids composés de fermions. Ce résultat est aussi essentiel pour le développement du calcul quantique, qui exige des systèmes à plusieurs particules dans un état quantique initial complètement défini.
|
[1] « Qantum tomography of an electron », T. Jullien, P. Roulleau, B. Roche, Y. Jin, A. Cavanna and D. C. Glattli, Nature 514, 603 (2014). |
|
|
[2] « Minimal-excitation states for electron quantum optics using levitons », J. Dubois, T. Jullien,P. Roulleau, F. Portier,P. Roche, Y. Jin, A. Cavanna W. Wegscheider, and D.C. Glattli, Nature 502, 659 (2013). Voir le fait marquant IRAMIS : « Les lévitons : des électrons sans bruit pour l’optique quantique électronique« |
|
|
[3] « Single electron quantum tomography in quantum Hall edge channels » Ch Grenier, R Hervé, E Bocquillon, F D Parmentier, B Plaçais, J M Berroir, G Fève and P Degiovanni, New Journal of Physics 13, 093007 (2011). |
Contact CEA : Christian Glattli, IRAMIS/SPEC – Groupe « Nanoélectronique ».
Collaboration: Groupe de Physique et Technologie des Nanostructures (PHYNANO), CNRS – Laboratoire de Photonique et de Nanostructures (LPN), Marcoussis (France).





