Tout objet dans un état de superstition d’états quantiques mais non isolé, perd sa cohérence (décohérence quantique) et seuls les états observables macroscopiquement sont finalement observables.
Des chercheurs du SPEC ont réussi pour la première fois à contrôler la cohérence quantique des électrons d’un conducteur (quasi-particules) en présence d’un champ magnétique intense (8 Teslas, i.e. en régime d’effet Hall quantique entier). Les longueurs de cohérence quantique ont pu être augmentées d’un facteur deux en modifiant le couplage du conducteur quantique avec son environnement, grâce à des grilles de polarisation judicieusement placées.
Le contraste des franges d’interférences en sortie d’un interféromètre électronique est un bon reflet de cette cohérence. Cette expérience a ainsi permis de comprendre la dépendance de la visibilité des interférences quantiques en fonction de l’énergie des électrons injectés.
Une des questions au cœur de la physique fondamentale des conducteurs quantiques est de déterminer à quel point les quasi-particules d’un conducteur se comportent comme des particules libres sans interaction. Un outil très utile à la compréhension de l’interaction d’une quasi-particule avec son environnement est de déterminer sa longueur de cohérence, c’est à dire la distance sur laquelle une quasi-particule perd sa cohérence quantique, reflet de ses propriétés ondulatoires.
Le régime d’effet Hall quantique entier, qui s’obtient à basse température (quelques dizaines de mK) en appliquant un fort champ magnétique (quelques Teslas) perpendiculairement à un gaz bidimensionnel d’électrons, constitue une plateforme expérimentale pour comprendre cette physique. En effet, dans un tel régime, le transport se fait par des fils unidimensionnels sur les bords du conducteur. Le transport est également chiral, ce qui veut dire que les électrons dans ces fils vont dans la même direction, mimant ainsi un faisceau d’électrons dans le vide.
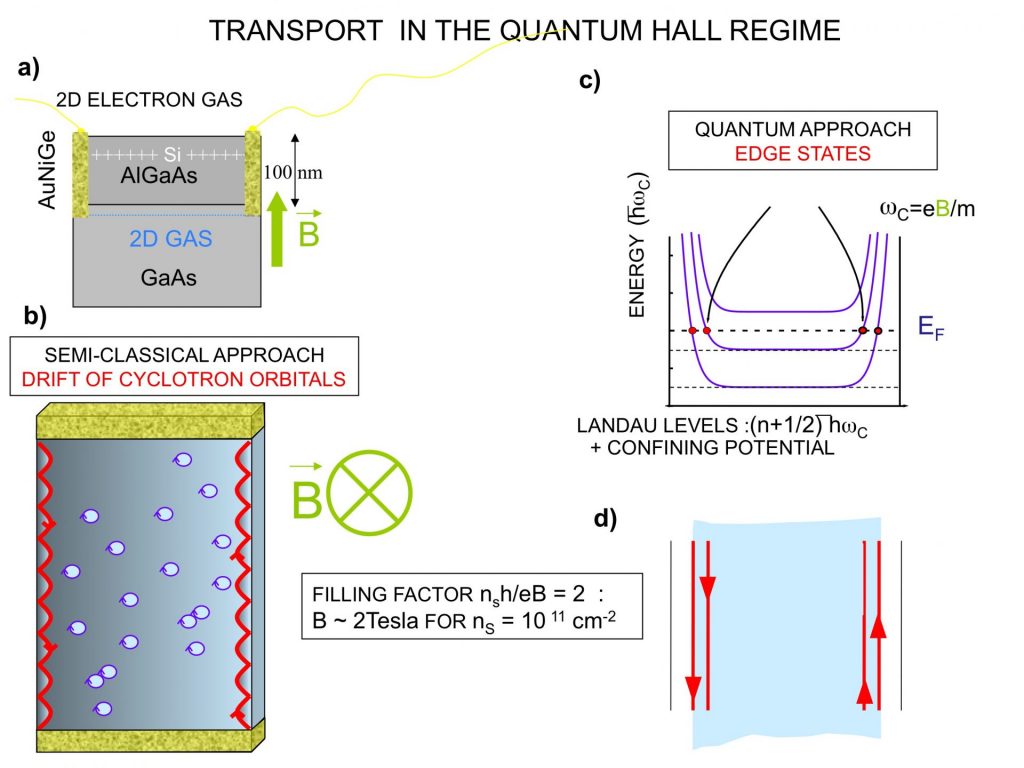
Figure 1: a) Les fils unidimensionnels chiraux mimant des faisceaux d’électrons sont obtenus en appliquant un fort champ magnétique perpendiculairement à un gaz bidimensionnel d’électrons dans GaAs/GaAlas. b) La chiralité peut être comprise comme le rebond successif des orbites cyclotrons sur le bord de l’échantillon ou c) comme le croisement des niveaux de Landau avec le niveau de Fermi. d) Ces fils sont localisés sur le bord de l’échantillon. Leur nombre est égal au nombre d’électrons par quantum de flux.
Le nombre de fils unidimensionnels sur le bord de l’échantillon dépend du nombre d’électrons par quantum de flux, nombre appelé facteur de remplissage. Pour un facteur de remplissage de 2, qui correspond à un champ magnétique de l’ordre de 2 Tesla pour une densité électronique de 1011 électrons par cm2, il y a deux fils chiraux rapprochés, de telle sorte que les deux fils sont en interaction.
Dans ce régime, on peut réaliser des interféromètres électroniques quantiques, équivalents à des interféromètres optiques mais avec des électrons et dans un conducteur. Les lames séparatrices utilisées en optique, correspondent ici à des grilles métalliques déposées à la surface de l’échantillon qui vont permettre de coupler deux états de bord où les électrons se propagent en sens inverse (contre-propagation). On obtient ainsi des interférences quantiques (amplitude relative des interférences) ayant une visibilité de l’ordre de 70 % à 15 mK.
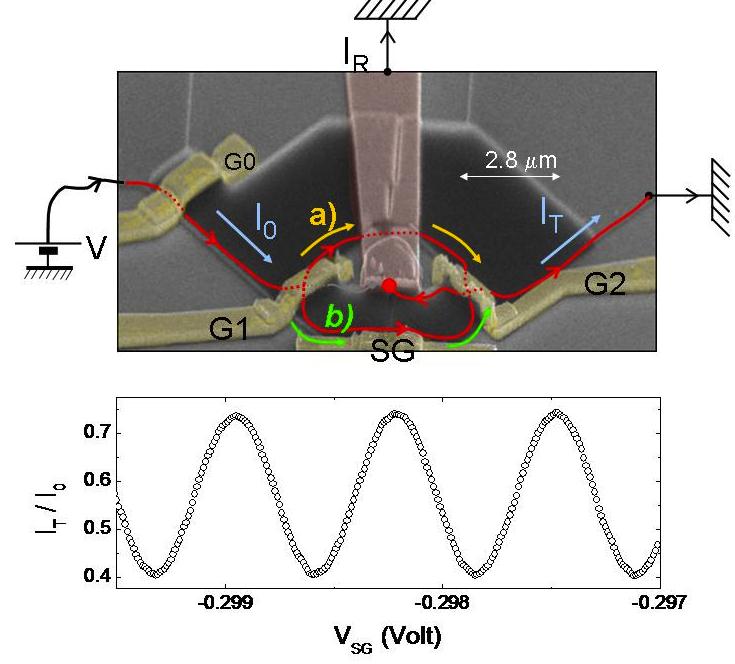
Figure 2 : Vue SEM d’un interféromètre électronique de Mach-Zehnder. Les grilles G1 et G2 sont l’équivalent des lames séparatrices de l’optique. La grille SG permet de changer la différence de longueur des trajets a) et b). Les interférences quantiques sont révélées par des oscillations dans le courant transmis IT lorsqu’on varie la tension grille VSG.
Le facteur limitant pour ces interférences est la perte de cohérence quantique due à l’interaction des quasi-particules du fil avec son environnement. Ces dernières années, les chercheurs du groupe NanoElectronique (GNE) du SPEC ont réussi, à déterminer pour la première fois la dépendance en température de cette longueur de cohérence [1], et à montrer que le bruit thermique de charge dans l’environnement [2] est à l’origine de cette décohérence.
Cette démonstration a été rendue possible car pour un facteur de remplissage de 2, l’environnement d’un des fils chiral est un autre fil chiral où les électrons se propagent dans le même sens (co-propagation). Une expérience « which path » [3] a été réalisée afin de mieux comprendre la cohérence des états de bords. Elle consiste à réduire l’amplitude des interférences quantiques en sondant la présence de la quasi particule interférant dans l’un des bras de l’interféromètre. Cette mesure projette alors la quasi particule sur un des bras, supprimant la superposition quantique de l’excitation sur les deux bras et par conséquent les interférences quantiques.
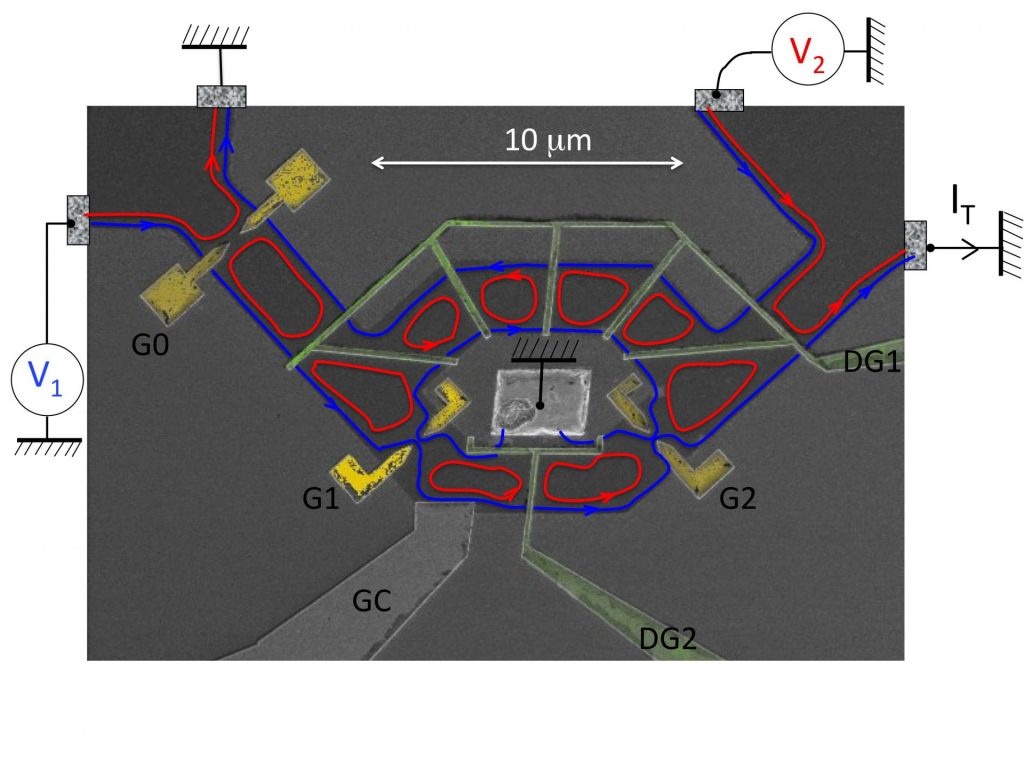
Figure 3: Interféromètre électronique de Mach-Zehnder modifié: Les grilles addionnelles DG1 et DG2 permettent de modifier le couplage entre les états de bord et ainsi de contrôler la cohérence quantique dans l’état de bord « bleu » au moyen d’une simple tension grille.
Ce fait marquant porte sur la dernière avancée de cette recherche : en contrôlant la forme et le couplage entre les deux états de bords, les chercheurs du GNE ont réussi à augmenter la cohérence quantique d’un facteur deux [4].
Dans l’échantillon visible sur la figure 3, l’état de bord interférant est représenté en bleu alors que l’état de bord qui correspond à son environnement est représenté en rouge. L’action principale des grilles additionnelles (DG1 et DG2) en forme de peigne est de localiser l’état rouge sur des trajectoires fermées. On écarte ainsi partiellement l’état rouge de l’état bleu, en modifiant leur couplage. Ce dernier est par ailleurs mesurable [4]. Sur la figure 4, on peut observer la transmission des états de bord à travers le peigne (cercles noirs) ainsi que la visibilité des franges d’interférences (en rouge) en fonction de la tension grille appliquée sur le peigne supérieur. La visibilité des franges d’interférence augmente énormément jusqu’à la formation des boucles rouges et diminue ensuite.
Un schéma représentant la configuration des états de bords est également représenté sur cette figure. Alors que l’augmentation de la visibilité traduit une augmentation de la longueur de cohérence, la diminution pour des valeurs plus négatives de DG1 traduit un déréglage de l’interféromètre.
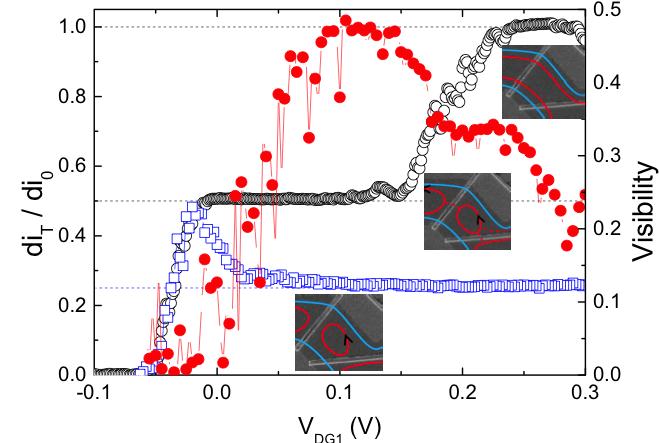
Figure 4 : Cercles ouverts (noirs) : transmission dIT/dI0 au travers de la structure en peigne permettant de suivre la fermeture de l’état de bord interne. Trois représentations schématiques des états de bord correspondant à la mesure de transmission sont représentées. La visibilité des interférences quantiques (points rouges) augmente jusqu’à la fermeture de l’état interne en boucles puis diminue. La diminution est due à un déréglage de l’interféromètre traduit par un écart des carrés bleus (valeur du courant moyennée sur une oscillation quantique) à 0.25 (échelle de gauche). Les chutes soudaines de visibilité sur la courbe rouge sont dues à un alignement des niveaux d’énergie des boucles rouges avec le niveau de Fermi, menant à un bruit de charge dans l’environnement délétère pour les interférences quantiques.
La prochaine étape de cette expérience sera de mesurer/contrôler la longueur de cohérence des quasi-particules injectées au dessus de la mer de Fermi.
Références :
- Direct measurement of the coherence length of edge states in the integer quantum hall regime,
P. Roulleau, F. Portier, and P. Roche, A. Cavanna, G. Faini, U. Gennser, and D. Mailly, Phys. Rev. Lett. 100, 126802 (2008). - Noise dephasing in edge states of the integer quantum hall regime,
P. Roulleau, F. Portier, and P. Roche, A. Cavanna, G. Faini, U. Gennser, and D. Mailly., Phys. Rev. Lett. 101, 186803 (2008). - Tuning decoherence with a voltage probe
P. Roulleau, F. Portier, and P. Roche, A. Cavanna, G. Faini, U. Gennser, and D. Mailly, Phys. Rev. Lett. 102, 236802 (2009). - Quantum coherence engineering in the integer quantum hall regime
P-A. Huynh, F. Portier, H. le Sueur, G. Faini, U. Gennser, D. Mailly, F. Pierre, W. Wegscheider, and P. Roche, Phys. Rev. Lett. 102, 256802 (2012).
Contacts :
P. Roulleau, F. Portier, and P. Roche, P-A. Huynh,
CEA, Nanoelectronic group, Service de Physique de l’État Condensé, CEA Saclay, F-91191 Gif-Sur-Yvette, France.
A. Cavanna, G. Faini, U. Gennser, and D. Mailly, H. le Sueur, F. Pierre,
CNRS, Phynano team, Laboratoire de Photonique et Nanostructures, Route de Nozay, F-91460 Marcoussis, France.



