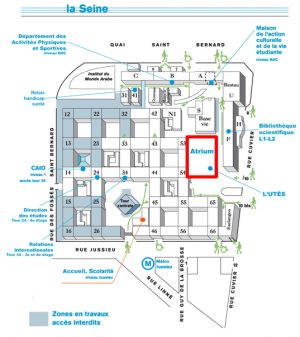
Soutenance dans la salle de visioconférence au RdC de l’Atrium du campus de Jussieu (Univ. Paris VI).
Les graphes des réseaux d’interactions sociales révèlent des propriétés topologiques dont nous cherchons à comprendre l’origine. Dans ce but nous manquons de références qui permettraient de construire une échelle de comparaison de leurs caractéristiques géométriques. Cette thèse propose une méthode générique pour produire des graphes synthétiques dont les propriétés sont ajustables, dans l’ambition de réaliser un balisage de l’espace des graphes.La méthode proposée dérive de procédures markoviennes dont l’étape élémentaire consiste à échanger les extrêmités de liens du graphe. Selon les contraintes imposées, une telle procédure doit être adaptée ; nous discutons alors des difficultés inhérentes à sa réalisation pratique et les moyens à notre disposition pour estimer sa validité. Puis nous rendons compte d’applications pratiques sur des réseaux technologiques, de collaborations, ou d’échanges commerciaux. Le principe mis en oeuvre dans ces illustrations consiste à construire une suite d’ensembles de graphes obéissant à des contraintes de plus en plus exigeantes ; puis à comparer les propriétés de chacun aux données réelles, a fin de déterminer quels éléments topologiques ont un rôle essentiel. Au fil des exemples, nous proposons des améliorations techniques de nos algorithmes qui permettraient d’en élargir les utilisations possibles.Cette méthode serait suffisamment générale pour pouvoir décrire des réseaux d’interactions d’une autre nature, mais aussi pour intégrer des informations supplémentaires à la description graphique telles que l’activité temporelle des agents ; nous proposons pour conclure quelques éléments de réflexion pour réaliser ces objectifs.