Comment mesurer un état quantique efficacement mais de manière aussi peu invasive que possible ? Nous avons abordé cette question de principe avec des expériences sur des circuits quantiques supraconducteurs dans lesquels nous avons observé comment la dynamique des transitions entre états quantiques était affectée par des mesures d’intensité variable.
Les états quantiques que nous avons sondés sont des états localisés, appelés états d’Andreev, présents dans toutes les jonctions entre supraconducteurs, que ce soit des jonctions tunnel (les jonctions Josephson), des jonctions via des métaux non-supraconducteurs, des constrictions, etc. Pour nous, les jonctions sont des contacts réduits à un seul atome entre deux électrodes supraconductrices. Ces jonctions sont obtenues à partir d’un pont en aluminium de quelques microns de long suspendu sur un substrat plastique souple (Fig. 1e). En pliant le substrat de manière très contrôlée, dans le vide cryogénique à 30mK, on étend le pont, qui s’affine, et on sait s’arrêter juste avant qu’il ne casse, quand le pont ne tient plus que par un seul atome. C’est ce qu’on appelle un « contact atomique », où apparaissent des états d’Andreev à des énergies inférieures au gap du supraconducteur, mais dépendant de la configuration de tous les atomes à proximité du contact. En répétant l’opération, on obtient à chaque fois des états d’Andreev avec des énergies différentes, ce qui permet de mesurer les mêmes effets dans différentes conditions.
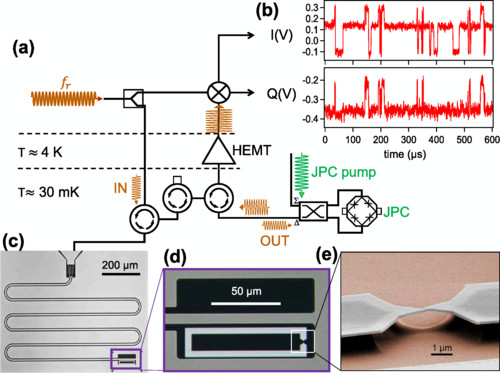
Figure 1 : Contrôle continu de l’état quantique d’un contact de taille atomique : (a) dispositif de mesure micro-onde : un signal micro-ondes continu à la fréquence fr du résonateur nu est envoyée à la cavité micro-ondes. Le signal réfléchi est amplifié à basse température par un convertisseur paramétrique Josephson (JPC), puis mélangé avec une tonalité d’oscillateur local pour obtenir les composantes homodynes I et Q de la réponse. Un point toutes les 10 ns est enregistré à l’aide d’une carte d’acquisition rapide, ce qui permet d’obtenir des traces temporelles telles que celles présentées en (b), qui montrent les sauts entre les états. (c) La cavité est un résonateur micro-ondes coplanaire d’un quart de longueur d’onde gravé dans un film de Nb de 150 nm d’épaisseur sur un substrat de Kapton. (d) Une boucle en aluminium est fabriquée près de l’extrémité court-circuitée du résonateur. (e) La boucle contient un pont suspendu étroit qui peut être aminci, sous vide cryogénique, en pliant le substrat, jusqu’à obtenir un contact atomique.
La méthode de choix pour mesurer les circuits quantiques est de les coupler à des résonateurs microonde de fort facteur de qualité (Fig. 1c), dont le rôle est double : d’une part ils filtrent le bruit extérieur, d’autre part ils permettent de mesurer l’état quantique du circuit, qui est révélé par la manière dont il décale la fréquence de résonance du résonateur. En pratique, on mesure l’amplitude des signaux en phase (I) et en quadrature (Q) d’une impulsion microonde à fréquence fixe réfléchie par la cavité, elle-même faiblement couplée à une ligne de mesure (Fig. 1a). Le résultat est représenté par un point dans le plan complexe. En répétant plusieurs milliers de fois le même protocole expérimental, on obtient des nuages de points (Fig. 2) dont les poids relatifs sont déterminés par les occupations statistiques des états et les coefficients des superpositions d’état. Dans le cas des états d’Andreev dans un contact atomique, il y a de manière générique 3 états : l’état fondamental (g), un état excité correspondant à une double occupation de l’état d’Andreev par une paire de Cooper excitée (e), et un état dit « impair » (o) dans lequel une quasiparticule unique occupe l’état d’Andreev.
Quand l’amplitude du signal de mesure est faible (Fig. 2, premier panneau à gauche), l’amplitude du signal réfléchi l’est aussi, et les trois nuages de point sont enchevêtrés. En augmentant l’amplitude (Fig. 2), les nuages se séparent de plus en plus et chaque mesure détermine de manière de plus en plus discriminante l’état du circuit. Mais on observe que le poids relatif des nuages varie avec l’amplitude de mesure, ce qui trahit une influence de la mesure sur la dynamique des transitions entre états.

Figure 2 : Histogrammes des valeurs de (𝐼,𝑄) enregistrées lors de mesures continues à différentes amplitudes du signal de mesure. (a) Contact avec une fréquence de transition de 6.33GHz, à des amplitudes de sonde relatives α0 croissantes. Dans chaque panneau, la couleur est associée à la valeur de α0, et la luminosité dans l’échelle des couleurs code le nombre de coups par pixel, avec une variation linéaire de 0 à 12000.
Pour caractériser cet effet, nous avons analysé de longues mesures continues montrant un grand nombre de transitions (un extrait est montré Fig. 1b) pour en déduire les taux de transition. C’est ainsi que nous avons déterminé l’évolution des taux de transition avec l’intensité de la mesure, et comparé quantitativement avec une théorie que nous avons étendue pour couvrir la large gamme de paramètres à laquelle nous avons accédé en répétant l’expérience sur plusieurs contacts atomiques.
Nos résultats quantifient l’effet de la mesure sur la dynamique des transitions entre états quantiques et permet d’optimiser l’intensité et la durée des mesures pour atteindre le meilleur compromis entre fidélité et discrimination.
Référence : Effects of measurement power on state discrimination and dynamics in a circuit-QED experiment. L. Tosi, I. Lobato, M. F. Goffman, C. Metzger, C. Urbina, and H. Pothier, Phys. Rev. Research 6, 023299 (2024). arXiv preprint arXiv: 2310.04556
Contact CEA-SPEC : Hugues Pothier, Marcelo Goffman et Cristian Urbina, groupe Quantronique, SPEC, IRAMIS
Ce travail a été financé par le contrat ANR JETS, et par le contrat FET-Open AndQC. L.T. a bénéficié de la bourse Marie Skłodowska-Curie n° 705467.




