Spin-orbit coupling offers many possibilities for converting spin signals into charge ones and vice versa. In particular, charge currents may be generated by pure spin injection via the spin galvanic effect — the conversion of a non-equilibrium spin accumulation into a charge current.
In certain settings, and notably in a novel generation of oxide-based experimental setups, spin injection takes place through an inversion symmetry-broken tunnel junction. Quantum coherent processes taking place under such barrier give rise to an anisotropic, non-local and (only apparently) non-reciprocal charge current generation.
A key concept in spintronics is that of « spin-charge interconversion ». In simple terms, this means the generation of electric currents by injecting spin angular momentum into a metallic systems, or vice versa. The interconversion arises from spin-charge correlations due to spin-orbit coupling, and may take place in very different settings, e.g. transition metals, doped semiconductors, the conducting surfaces of 3D topological insulators or the two-dimensional electron gases (2DEGs) existing at some oxide interfaces.
Charge currents are typically generated via the inverse spin Hall effect and the spin galvanic effect. In the first case the electric current appears in response to a transverse pure spin current — the flow of spin angular momentum without any associated charge flow. In the second one it is a consequence of a non-equilibrium spin accumulation.
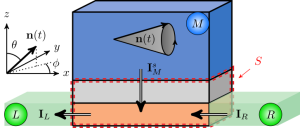
Now consider the standard spin pumping setup sketched in Fig. 1: the top magnetic electrode (M) is driven, and its precessing magnetisation injects angular momentum — but no charge — into the underlying metallic system, where spin-orbit coupling converts it into a measurable voltage drop between two other electrodes (L and R). If the receiving system (orange layer) is two-dimensional the injected spin cannot flow away from the magnet but simply accumulates in the two-dimensional layer: there is no spin Hall effect, and only spin galvanic conversion is possible.

The injection process itself is however non-trivial, as it happens through the inversion-asymmetric magnetic tunnel junction (gray layer) separating the top electrode from the 2DEG. To describe such a generalised spin galvanic conversion one has to consider the full spin-active structure, consisting of the magnetic injector, asymmetric tunnel barrier and spin-orbit coupled 2DEG The key point is that under-the-barrier transmission is not only spin-sensitive, but also skewed in momentum space — « up » electrons tunnel better « going left », while « down » electrons do so « going right ». This is a consequence of spin-orbit coupling within the barrier and on the 2DEG side, furthermore affected by the presence magnetism. Since the internal spin-orbit field is anisotropic, conversion should also be so.
Indeed, the LNO group at SPEC recently measured a strongly anisotropic conversion in the 2DEG at the LaAlO3|SrTiO3 interface, carrying imprints of the internal effective spin-orbit field. This contrasts however with the known fact that the Onsager reciprocal phenomenon — the generation of a non-equilibrium spin accumulation by driving a current — is isotropic in the very same kind of systems.
To explain such an anisotropic response, and to clarify the apparent breakdown of Onsager reciprocity, we developed a theory of spin-charge conversion for multi-terminal setups in which a driven magnetic electrode acts as a pure spin injector — so that only spin angular momentum but no net charge flows through the tunnel barrier and into the underlying spin-orbit coupled 2DEG. The theory respects by construction Onsager constraints, and allows to identify a spin-charge conversion channel mixing skew-tunneling and standard spin galvanic physics which we dubbed « tunneling anisotropic spin galvanic effect ». The general theory was tested in a model system for a LaAlO3|SrTiO3 spin pumping setup, see Fig. 2, validating certain phenomenological arguments describing the experiments and establishing that the anisotropic spin-charge conversion is robust to impurity scattering.

References : Tunneling anisotropic spin galvanic effect, G. Fleury, M. Barth, C. Gorini, Phys. Rev. B 108, L081402 (2023)
Contact CEA : Cosimo Gorini, Modeling and Theory Group (SPEC/GMT)
Collaboration :
• Service de Physique de l’Etat Condensé (SPEC), UMR 3680 CEA-CNRS, Université Paris-Saclay
• Institute of Theoretical Physics, University of Regensburg, Germany