La crise d’ébullition comme un phénomène critique

Etudier un fluide près du point critique liquide-gaz et en microgra­vité permet de profiter du ralentissement critique pour observer la crise d’ébullition, un phénomène en même temps énigmatique et important pour les échangeurs de chaleur industriels. L'observation de ce ralentissement nous a permis de découvrir un régime précédant immédiatement la crise d’ébullition : dans ce régime, la partie asséchée de la paroi chauffante, située sous les bulles de vapeur, forme des amas de percolation de structure fractale.

Quand on chauffe de l’eau dans une casserole, des bulles de vapeur naissent progressivement au fond. Si on pouvait augmenter encore plus fortement la puissance de chauffage, une pellicule de vapeur apparaîtrait brutalement entre le fond de la casserole et l’eau. Ce phénomène s’appelle la crise d’ébullition. Impossible à réaliser dans une cuisine, cette transition existe bien en milieu industriel. Elle est très dangereuse car elle provoque une hausse très importante de la température de la paroi chauffante et peut conduire à sa fusion. La dynamique d’assèchement de la paroi chauffante est extrêmement fugace et difficile à visualiser. On peut la ralentir en réalisant les expériences au voisinage du point critique, où la diffusivité thermique diminue et où la croissance des bulles de vapeur sur la paroi devient donc plus lente. Mais il faut également réduire la gravité, car la tension superficielle diminuant, les bulles de vapeur ne peuvent plus exister sous la gravité terrestre.

L’expérience a été réalisée au voisinage du point critique de H₂ (33 K, 13 bar) en utilisant le banc HYLDE (HYdrogen Levitation DEvice) au Service des basses températures du CEA-Grenoble. La gravité est compensée dans l’hydrogène par le champ magnétique B d’une bobine supraconductrice de 8T : en effet, la force volumique totale f exercée sur le fluide s’écrit : $f=\frac{\mathrm{\chi }}{\mathrm{2\mu ₀}}{\mathrm{\nabla (B}}^2\mathrm{)+\; <em>\rho g</em>}$ , où χ et ρ sont respectivement la susceptibilité magnétique et la densité du fluide, g la gravité et μ₀ la perméabilité du vide. Puisque χ est proportionnelle à la densité ρ, la valeur de ${\mathrm{\nabla (B}}^2)$ nécessaire pour satisfaire la condition f = 0, est indépendante de ρ. Cela signifie que la gravité peut être compensée simultanément dans les phases gazeuse et liquide.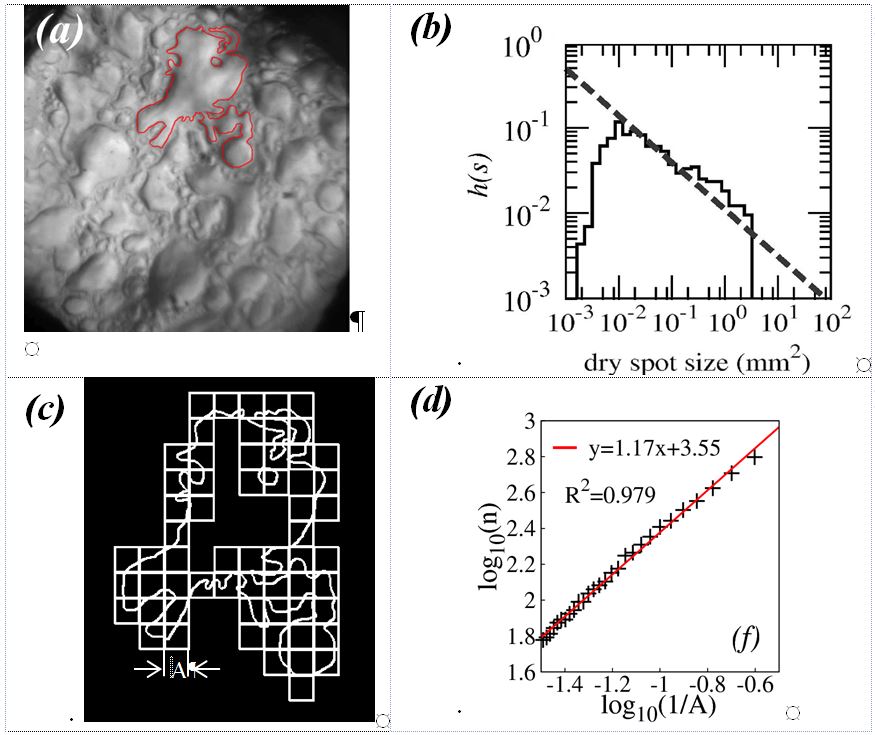

La dynamique de l’assèchement (Fig1a) a été observée à travers une paroi transparente chauffée par un courant électrique injecté dans un film conducteur, également transparent. Nous avons mis en évidence un nouveau régime de croissance des parties sèches de la paroi chauffante qui apparaît juste avant la crise d’ébullition. Il est caractérisé par l’apparition d’amas secs percolants. Le traitement des images de la paroi montre que la taille des amas est distribuée selon une loi de puissance et que les contours possèdent des propriétés fractales (Fig. 1). Il s’agit de la signature de la dynamique critique, situant ainsi la crise d’ébullition dans la catégorie des phénomènes critiques et des lois d’échelle universelles.

Référence :

Criticality in the slowed-down boiling crisis at zero gravity,
T. Charignon, P. Lloveras, D. Chatain, L. Truskinovsky, E. Vives, D. Beysens, and V. S. Nikolayev, Phys. Rev. E 91, (2015) 053007

L’article a été présenté sur la page de kaléidoscope de Phys. Rev. E en mai 2015.

---

Collaboration : T. Charignon¹, P. Lloveras², D. Chatain¹, L. Truskinovsky², E. Vives³, D. Beysens^1,4, and V. S. Nikolayev^5,*

Contact CEA  : Vadim Nikolayev – SPEC/SPHYNX