La turbulence dans un fluide est un phénomène familier, qui se caractérise par la présence de tourbillons de toutes tailles et un comportement désordonné et imprédictible. Losrqu’on augmente le nombre de Reynolds (Re), grandeur sans dimension donnée par le rapport entre forces d'inertie et forces visqueuses, on distingue différents régimes d'écoulement, depuis l'écoulement laminaire, puis chaotique jusqu'à l'état pleinement turbulent, dans lequel on observe une cascade d’énergie des grandes échelles d’injection à l’échelle de dissipation (cascade de Kolmogorov).
De nouvelles expériences modèles d'études de la turbulence, réalisées par l'équipe SPHYNX de l'IRAMIS/SPEC, ont permis de mettre en évidence de façon inattendue un comportement chaotique dans le régime de turbulence développée (i.e. à très grand nombre de Reynolds),. Ce résultat inattendu, conduit à nous interroger sur l'origine des situations d'intermittence que l'on observe en météorologie, dans les océans ou les turbines industrielles.
Le comportement d'un fluide que l'on agite est complexe et subit lorsque l'on augmente l'agitation une suite des transitions aujourd'hui clairement établies : à basse vitesse (nombre de Reynolds Re de l'ordre de 2 000), la viscosité domine l'écoulement laminaire du fluide. Au-delà d'un seuil d'agitation (Re > 2 000), les forces d'inerties dominent le système et le flux devient turbulent. La vision communément admise jusqu'à aujourd'hui est que cette turbulence augmente avec l'agitation : plus l'agitation est forte, plus la structure turbulente sera complexe, permettant une cascade efficace de l'énergie globalement fournie des grandes vers les petites échelles où elle est finalement dissipée.
Entre les deux régimes extrêmes, des comportements intermédiaires peuvent se développer présentant des structures tourbillonnaires stables ou oscillantes, pouvant présenter des comportements chaotiques à petit nombre de degrés de liberté (< 10), infiniment sensibles aux conditions initiales. Mais une fois le régime turbulent atteint, le désordre engendré semblait pouvoir être décrit comme celui d'un système uniformément agité, qui retrouve toutes ses symétries, avec un nombre très important de degrés de liberté (de l’ordre de 1014 à Re= 106).
On observe cependant dans différents systèmes réels à très grand nombre de Reynolds (météo, sillages de bateaux ou d’iles, … ou encore turbines industrielles) des régimes turbulents, oscillants de manière chaotique entre plusieurs régimes stationnaires. C’est le cas en particulier de la circulation zonale et bloquée qui caractérise le comportements des anticyclones dans l’hémisphère nord. Ce comportement chaotique est-il lié à la sensibilité de ces systèmes complexes à des conditions externes fluctuantes, ou les états moyens du fluide turbulent sont-ils intrinsèquement instables ?
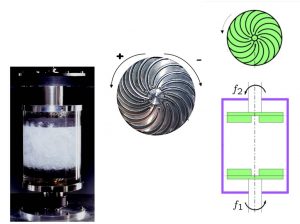
Pour répondre à ce type de question, l'équipe Sphynx de l'IRAMIS/SPEC a conçu une expérience modèle d'écoulement dit de « von Karman » : un fluide dans un cylindre est agité par deux turbines contra-rotatives (voir figure) et le vecteur vitesse en chaque point du fluide dans un plan méridien est mesuré par « Particle Image Velocimetry ». Pour une excitation symétrique des turbines, le schéma classique vers la turbulence est observé : écoulement laminaire, tourbillons stationnaires, oscillants, puis chaotiques, et enfin turbulent.
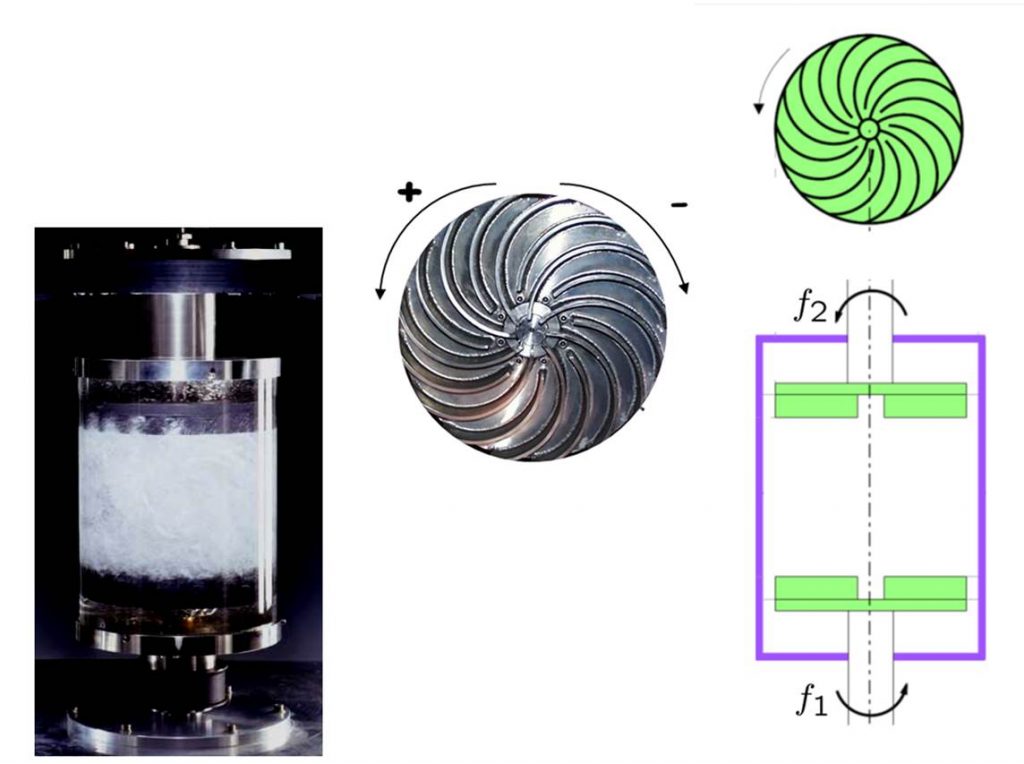
Ci-contre, en haut : trajectoire du système dans le plan θ-γ lors d'une excitation à fréquences imposées. Cycle d'hystérésis parcouru en faisant varier θ, la différence de fréquence de rotation des turbines haut et bas. En bas : trajectoire pour une excitation des deux turbines à couples constants.
L'étude s'est poursuivie en imposant au système une excitation asymétrique et en imposant soit des fréquences fixes aux deux turbines, soit des couples moteurs constants. Cette brisure de symétrie a des conséquences imprévues :
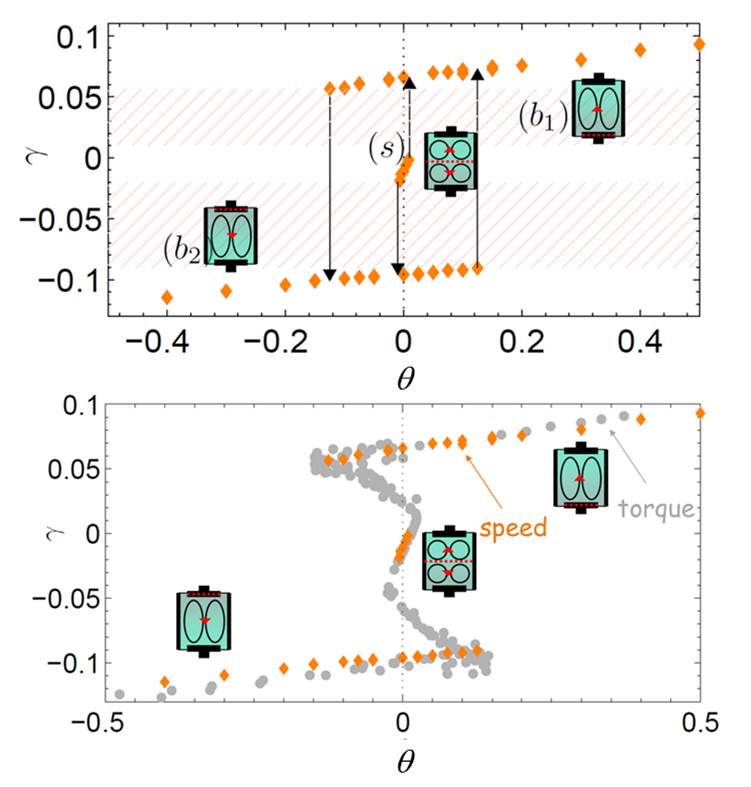
- Pour une excitationà fréquences imposées, la différence adimensionnée de couple moteur g, en fonction de l'écart de fréquence entre les 2 turbines q, présente un cycle d'hystérésis marqué. On peut aussi noter qu'il n'est pas possible de revenir en dynamique à la situation de départ (q = 0), résultant de l'excitation symétrique initiale : l’état turbulent garde en quelque sorte la mémoire de son histoire.
- Pour une excitation à couples imposés, le cycle dans le plan θ-γ est complétement différent et ne montre plus d'hystérésis (voir figure). À noter les zones à pente négative, où une diminution de la différence de couple moteur entraine une augmentation de la différence de fréquence de rotation.
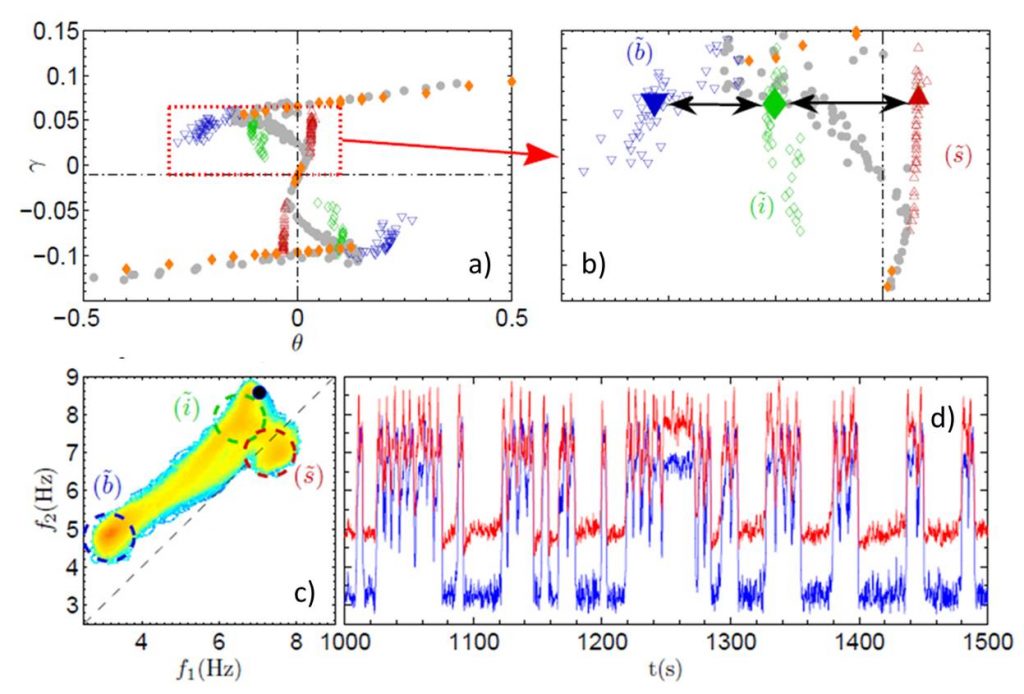
Enfin dans ce régime, selon la valeur de γ imposée, on observe le basculement dans le temps entre plusieurs configurations momentanément stationnaires, dont l'analyse montre un comportement typiquement chaotique.
Cette observation sur un système modèle bien contrôlé de régimes multi-stables dans le domaine turbulent, ouvre de nouvelles questions très profondes sur la nature de la turbulence, et conduit à la proposition suivante : « un système hydrodynamique pleinement turbulent (à nombre de Reynolds Re grand) peut avoir plusieurs états statistiquement stables et être intrinsèquement chaotique ». Si le caractère générique d'une telle affirmation peut être prouvé, alors tout système météorologique peut être intrinsèquement instable et le dimensionnement de turbines hydrauliques doit tenir compte de l'ensemble des régimes possibles et des sauts associés, pour résister aux fortes variations rapides de couple qui en résultent. Ce type d'étude se poursuit aujourd'hui par la recherche du bon modèle pour décrire les états et la dynamique de ces systèmes hydrodynamiques modèles « hors équilibre ».
Références :
– Evidence for forcing-dependent steady states in a turbulent swirling flow,
B. Saint-Michel, B. Dubrulle, L. Marie, F. Ravelet, and F. Daviaud, Physical Review Letters, 111 (2013) 234502.
– A zero-mode mechanism for spontaneous symmetry breaking in a turbulent von Kármán flow,
B Saint-Michel, F Daviaud and B Dubrulle, New J. Phys. 16 (2014) 013055.
– Influence of Reynolds number and forcing type in a turbulent von Kármán flow
B. Saint-Michel, B. Dubrulle, L. Marié, F. Ravelet and F. Daviaud, New Journal of Physics 16 (2014) 063037.
Contact CEA : François Daviaud (SPEC – UMR 3680 CEA-CNRS).