Comment un banc de poissons passe-t-il d’un comportement collectif à l’autre ?

Collaboration entre l’IRAMIS/SPEC du CEA et le Centre de Recherches sur la Cognition Animale (UMR 5169, UPS – CNRS)

En collaboration avec des biologistes et physiciens du Centre de Recherches sur la Cognition Animale de Toulouse, l'équipe de Hugues Chaté (IRAMIS/SPEC/SPHYNX) a construit puis étudié un modèle permettant de simuler numériquement la dynamique collective d'un banc de poissons. Contrairement aux nombreux autres modèles proposés dans la littérature pour l’étude des mouvements collectifs d’espèces grégaires (souvent intéressants pour le théoricien mais peu réalistes), ce modèle a été élaboré après avoir longuement analysé le comportement de poissons en bassin et ainsi identifié la nature des interactions entre individus. Il prédit l’existence de différentes phases dynamiques collectives (de type « essaim », « banc » ou « vortex »), en accord avec les observations expérimentales. Les résultats montrent que le passage d’une phase à une autre est déterminé par la vitesse des poissons et leur tendance à rester proches les uns des autres (interaction attractive) en pointant dans une même direction (interaction d’alignement).

Chez de nombreuses espèces grégaires, se mouvoir efficacement est une question de survie. La dynamique du groupe doit pouvoir alterner rapidement entre différentes phases selon les circonstances : déplacement rapide et coordonné du troupeau, formation de vortex ou simple agrégation sans mouvement global. Ces comportements collectifs sont dits émergents car l'apparition de l'ordre global ne nécessite aucune hiérarchie apparente au sein du groupe mais repose uniquement sur des interactions simples à l'échelle des individus. L'enjeu est alors d'identifier la nature des interactions et les mécanismes liés aux changements de régimes dynamiques.

Depuis près de vingt ans, l'intérêt pour ces phénomènes collectifs s'est diffusé au-delà de la communauté des biologistes : les physiciens, considérant les troupeaux en mouvement comme un nouvel état de la matière (la matière active) ont investi ce champ d'étude en proposant une grande variété de modèles théoriques ou numériques, inspirés de l'hydrodynamique et de la physique statistique hors-équilibre. Parmi ceux-ci figure par exemple l'emblématique modèle de Vicsek [1]. Toutefois ces modèles sont construits à partir d'hypothèses simplistes, en ne raisonnant parfois que sur les symétries du problème. S’ils sont d'un grand intérêt théorique, il est difficile de les confronter quantitativement aux observations biologiques.

Le modèle considéré ici [2] se distingue en ce qu'il est le fruit d'une collaboration étroite entre biologistes expérimentateurs et physiciens théoriciens. Les premiers ont récolté une grande quantité de données issues de l'enregistrement de la trajectoire de poissons (Kuhlia Mugil) évoluant collectivement dans un bassin. A partir de l'analyse statistique de ces données, les seconds ont identifié les interactions mises en jeu et ont construit un modèle décrivant la dynamique du banc. Chaque poisson nage à une vitesse constante mais en tournant de manière persistante. A chaque instant, la vitesse de rotation du poisson s'ajuste en fonction de la configuration de son entourage, afin de s'aligner avec ses voisins ou de rester proche d'eux. Ces interactions d'alignement et d'attraction sont pondérées par des paramètres dont il est possible d'ajuster les valeurs grâce aux données expérimentales.

Fig.1 – Banc de poisson formant un vortex (image issue de la vidéo attachée à la référence [3]).

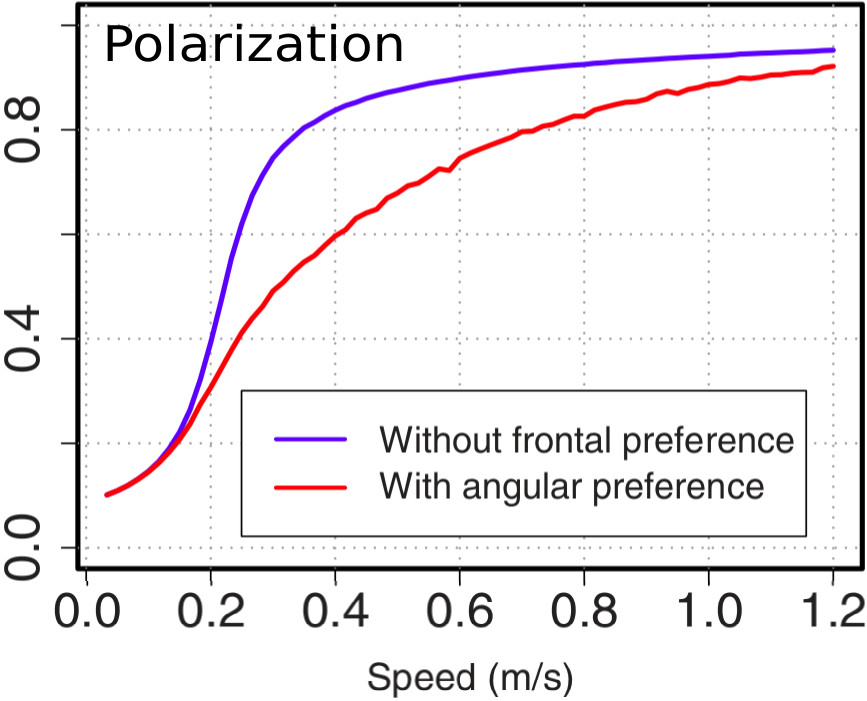
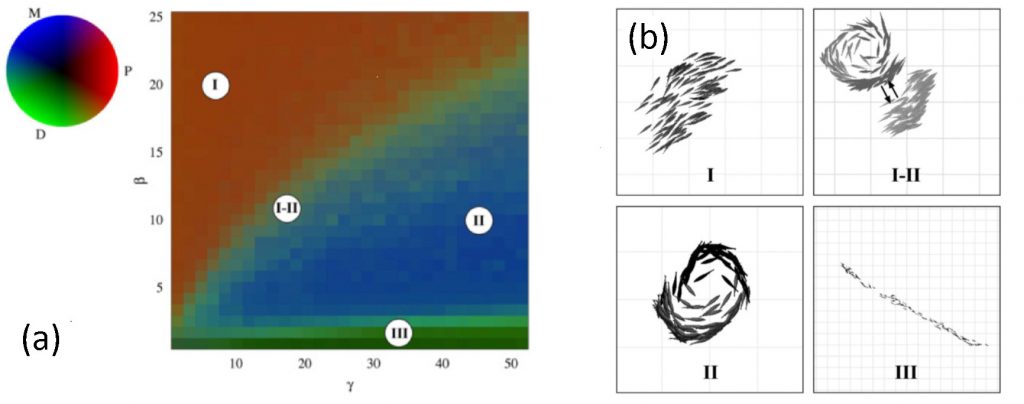
Dans une publication récente [3], nous présentons une étude numérique de ce modèle, ainsi qu'une variante dans laquelle est introduite une préférence frontale de l'interaction (dans ce cas, les poissons sont surtout influencés par leurs voisins situés devant eux). Dans les deux variantes du modèle, nous observons l'existence d'une transition de phase entre deux comportements collectifs lorsque la vitesse des poissons augmente (voir Fig.2) : à faible vitesse c'est un régime grégaire mais sans mouvement global (« swarming ») qui domine, mais lorsque la vitesse individuelle augmente, une phase de mouvement collectif émerge (« schooling » [Fig.3(b)-I]). Ces résultats sont en accord avec les observations expérimentales.Nous montrons également que l'émergence de structures en vortex (« milling » [Fig.3(b)-II]) est favorisée par l'hypothèse plus réaliste d'une préférence frontale. Une exploration systématique de l'espace des paramètres quantifiant l'alignement et l'attraction permet d'établir un diagramme des phases recensant les différents comportements collectifs possibles du banc [Fig.3(a)]. Il apparaît qu’un déplacement collectif global du groupe nécessite que l'interaction d'alignement domine. En revanche, lorsque l'attraction vers les voisins frontaux est privilégiée, le groupe se met à tourner en adoptant une forme de vortex. La transition entre ces deux phases est intermittente [Fig.3(b)-I+II] : le groupe peut donc éventuellement passer très rapidement d'un régime collectif à l'autre. C'est ainsi qu'en ajustant sa vitesse, ou en pondérant les différents types d'interaction avec ses plus proches voisins, le poisson se trouve emporté dans un mouvement collectif ou dans un autre. Cette étude est l'une des rares dans ce domaine à établir un lien direct entre un modèle et des données biologiques.

Fig.2 – Paramètre d’ordre polaire (quantité proportionnelle à la vitesse moyenne du banc) en fonction de la vitesse d’un poisson.

Fig.3 – (a) Diagramme des phases. Les paramètres β et γ quantifient respectivement les interactions d’alignement et d’attraction. Ils sont normalisés par les longueurs et les temps caractéristiques du modèle. (Rouge : mouvement collectif, bleu : vortex, vert : phase transitoire ou désordonnée, filaments). (b) Configurations typiques du groupe associées aux différentes régions du diagramme des phases.

JW Player goes here

Fig.4 – Simulations numériques avec 100 poissons, respectivement dans les régions I, II, I-II et III du diagramme de phase (de gauche à droite). Vidéos sous licence Creative Commons.

Contact CEA-IRAMIS : Hugues Chaté, IRAMIS/SPEC, groupe SPHYNX

Références :

[1] Novel type of phase transition in a system of self-driven particles,
T. Vicsek, A. Czirók, E. Ben-Jacob, In. Cohen et O. Shochet, Phys. Rev. Lett. 75 1226 (1995)

[2] Deciphering interactions in moving animal groups,
J. Gautrais, F. Ginelli, R. Fournier, S. Blanco, M. Soria, H.Chaté et G. Theraulaz,
PLoS Comput. Biol. 8:e1002678 (2012)

[3] Swarming, schooling, milling: phase diagram of a data-driven fish school model
D.S. Calovi, U. Lopez, S. Ngo, C. Sire, H. Chaté et G. Theraulaz, New J. Phys. 16 015026 (2014)

Voir aussi :

[4] Emergent spatial structures in flocking models: A dynamical system insight
J.-B. Caussin, A. Solon, A. Peshkov, H. Chaté, T. Dauxois, J. Tailleur, V. Vitelli, and D. Bartolo
Phys. Rev. Lett. 112, 148102