Afin de traiter correctement la dynamique de spin pour des nano-objets, le Groupe Modélisation et Théorie du SPEC, en collaboration étroite avec une équipe du CEA/DAM, Le Ripault, a mis au point un modèle générique décrivant à l’échelle atomique la dynamique spatiale des atomes couplée à leur aimantation de spin. Sur cette base, il est possible de rendre compte, à l'aide d'un code de dynamique moléculaire magnétique optimisé, de détails fins du magnétisme du cobalt massif et de l'évolution rapide du magnétisme d'îlots nanométriques.

Depuis la première expérience de Joule il y a plus de 150 ans démontrant qu’une substance pouvait se déformer sous l'effet d'un champ magnétique, on sait que les propriétés magnétiques des matériaux sont fortement connectées à leur structure cristallographique. Cette propriété intrinsèque peut se manifester de différente manière. Au niveau macroscopique les systèmes ferromagnétiques peuvent se déformer mécaniquement sous l’effet d’un champ magnétique. On parle alors de magnétostriction. Ces mêmes matériaux présentent également un effet magnéto-mécanique (ou magnétostrictif inverse) qui se caractérise par la modification de leur susceptibilité magnétique en présence de contraintes mécaniques. A l’échelle atomique, il est aussi bien connu que le magnétisme influence les propriétés cristallographiques des matériaux. C’est par exemple la présence de magnétisme qui stabilise la structure cubique centrée du fer. Réciproquement, la présence de défauts modifie de manière importante ses propriétés magnétiques [1]. Le couplage entre magnétisme et propriétés mécaniques des matériaux peut donc être précisément caractérisé à l’échelle atomique et moléculaire.
Nous avons alors mis au point un modèle générique en dynamique moléculaire décrivant à l’échelle atomique la dynamique spatiale des atomes couplée à leur aimantation de spin [2], [3]. Dans ce formalisme, l’énergie du système est la somme de deux termes : un Hamiltonien mécanique effectif décrivant l’énergie d’un ensemble d’atomes et un Hamiltonien de type Heinseberg généralisé, rendant compte de l’interaction d’échange magnétique entre sites atomiques ainsi que de l’anisotropie magnéto-cristalline. Le couplage entre le réseau et les spins intervient d’abord par l'intermédiaire d'un tenseur décrivant l'interaction d’échange fonction de la distance interatomique entre deux sites magnétiques. La magnétostriction est quant à elle restituée par la variation du terme d’anisotropie magnétique tant dans la direction que prennent les spins environnant que de la distance qui les sépare.
Un travail algorithmique important [2] s'est révélé nécessaire pour optimiser le processus d’intégration des équations du mouvement afin de le rendre à la fois efficace et sur des critères précis. Nous avons profité de la structure particulière des équations couplant le mouvement des atomes et les spins pour les combiner en un ensemble d’intégrateurs unifié. Par ailleurs, ces algorithmes permettent de modéliser aussi bien des ensembles micro-canoniques (où l’énergie reste constante dans le temps) que des ensembles canoniques plus réalistes pour lesquels la température et même la pression peuvent être contrôlées à l’aide d’un thermostat et d’un barostat. Ce travail d’implémentation a été transféré au sein d’un très grand code (plusieurs centaines de milliers de lignes) de simulation moléculaire utilisé par une large communauté : le code LAMMPS (http://lammps.sandia.gov/).
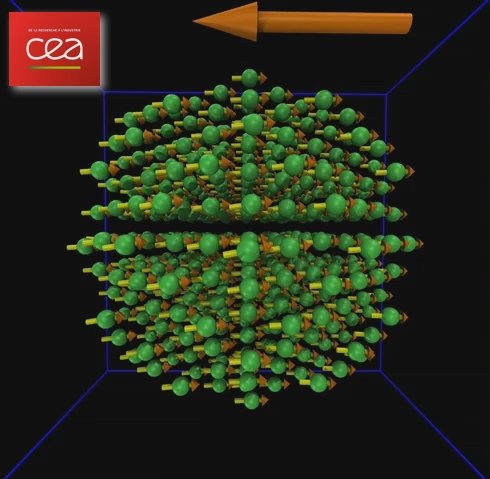
Vidéo montrant la dynamique de retournement magnétique d’une nano-sphère de 2.5 nm de diamètre de cobalt, sous l'effet d’un champ magnétique externe (flèche orange, 1 Tesla). On observe le caractère incohérent de la rotation d’aimantation et la prise en compte de la magnéto-élasticité qui fait vibrer les atomes autour de leur position d’équilibre, supposée stable à température nulle.
Nous avons ensuite appliqué ce modèle à différents systèmes magnétiques usuels à base de cobalt massif et en îlots sur un substrat et qui présentent un fort intérêt applicatif.
L'algorithme élaboré est ainsi capable de reproduire un effet aussi fin que le renversement avec la température de l’axe d’aimantation facile du cobalt hexagonal compact. Nous nous sommes ensuite intéressés à l'étude du cas plus complexe d’un îlot de cobalt déposé sur une surface de platine [3], système pour lequel des résultats expérimentaux spécifiques ont été obtenus. Les résultats concernant le comportement magnétique de ces systèmes différent notablement de ceux obtenus par les modèles simplifiés utilisés jusqu’à présent, ce qui montre leurs limitations. Les différents régimes de renversement d’aimantation en fonction de la taille du système sont notamment très bien mis en évidence, et montrent parfaitement le régime super-paramagnétique de ces îlots.
Ce travail de modélisation ouvre la voie à de multiples applications en nanomagnétisme dans l’étude de la cinétique de retournement ultra-rapide de l’aimantation, que dans l’optoélectronique et magnétique en régime terahertz. Il devrait aussi donner lieu à de nouveaux développements fondamentaux car il reste encore de nombreuses questions ouvertes (notions de température de configuration de spin, nature du bruit dans une dynamique stochastique etc …) dans ce domaine émergent.
Reférences :
[1] Vacancy and substitutional impurities in the spin-density wave state of Cr from first principles
R. Soulairol, Chu-Chun Fu et C. Barreteau, Phys. Rev. B 83, 214103 (2011).
[2] Anisotropic magnetic molecular dynamics of cobalt nanowires
D. Beaujouan, P. Thibaudeau et C. Barreteau, Phys.Rev.B 86 (2012) 174409
[3] Thermal behavior of superparamagnetic cobalt nanodots explored by anisotropic magnetic molecular dynamics simulations
D. Beaujouan, P. Thibaudeau et C. Barreteau, J.Appl.Phys. 111 (2012) 07D126.
Contacts :
- IRAMIS/SPCSI : Cyrille Barreteau (IRAMIS/SPCSI/LNOSC).
- CEA/DAM, Le Ripault : Pascal Thibaudeau.



