P.P. Cortet, E. Herbert, A. Chiffaudel, F. Daviaud, B. Dubrulle, V. Padilla
Contact: F. Daviaud
En étudiant la réponse d’un écoulement pleinement turbulent à une brisure de symétrie de son forçage, sur une gamme de nombre de Reynolds, Re, allant de 150 à 106, nous avons récemment mis en évidence pour Re = 40 000 une transition de phase analogue à la transition para-ferromagnétique. De plus, cette transition est associée à un maximum de l'amplitude des fluctuations de la symétrie de l'écoulement et correspond à des brisures intermittentes et spontanées de symétrie entre différents états métastables.Les transitions de phase sont un phénomène omniprésent dans les systèmes physiques et sont généralement associées à des brisures de symétries. La symétrie gouverne également la transition vers la turbulence: lorsque le nombre de Reynolds augmente, une succession de bifurcations brise les diverses symétries de l'écoulement laminaire. À grand nombre Reynolds, il est couramment admis que toutes les symétries brisées sont statistiquement restaurées et l’on peut se demander si cet écoulement turbulent ne peut pas être lui-même le siège de bifurcations entre différents états moyens, qui pourraient être interprétées en termes de transition de phase.
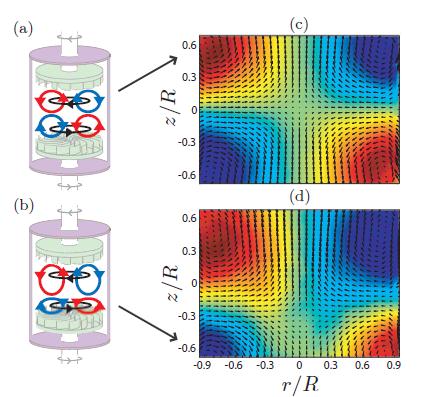
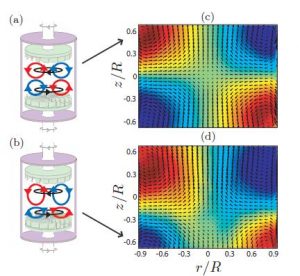
Notre montage expérimental est constitué d'un cylindre de Plexiglas® rempli d'un mélange eau-glycérol. Le liquide est mécaniquement entrainé par deux turbines coaxiales tournant en sens opposé (cf. Fig. 1). Les mesures de vitesse sont réalisées avec un système de PIV stéréoscopique fournissant les 3 composantes de la vitesse dans un plan méridien. Les paramètres de contrôle sont le nombre de Reynolds Re = (f1+f2)R2/ν avec ν la viscosité du fluide et fi la fréquence de rotation des turbines et θ = (f1-f2)/ (f1+f2) qui contrôle l'asymétrie du forçage.
 |
 |
|
|
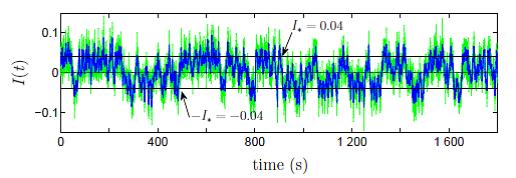
Figure 2 : Moment angulaire global I(t) pour Re = 43 000 et Θ = 0. La ligne verte/claire provient de l'acquisition PIV à 15 Hz et la ligne bleue est filtrée passe-bas à 1 Hz. On a représenté des lignes à I(t)=± I*= ± 0.04 qui correspondent à la momentisation turbulente. |
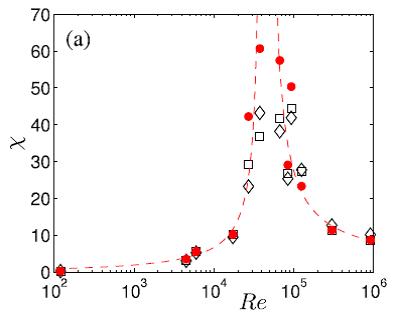
Figure 3 : Susceptibilité χ à la brisure de symétrie en fonction du nombre de Reynolds Re à Θ = 0. |
La symétrie de l’écoulement peut être caractérisée de façon quantitative par 2 scalaires : la position de la couche de cisaillement et le moment angulaire global I, deux quantités statistiquement équivalentes. Nous avons montré que la réponse de l’écoulement à une faible dissymétrie de forçage était linéaire, avec une pente qui dépendait du nombre de Reynolds : le coefficient de réponse croit avec Re et présente une divergence à un nombre de Reynolds critique Rec = 40 000 avant de redécroitre au-delà. Cette divergence coïncide avec un changement des propriétés statistiques de la symétrie de l’écoulement instantané : la pdf de I(t) devient non Gaussienne avec des maxima multiples, révélant des états métastables non symétriques. Pour un forçage symétrique, on observe également un pic de fluctuations de I(t) à Rec : ces fluctuations correspondent à des intermittences temporelles entre des états métastables de l’écoulement qui, contrairement à l’écoulement moyen –moyenné sur de très longs temps-, brisent spontanément la symétrie du système. Ces observations peuvent entre interprétées en terme de divergence de la susceptibilité à la brisure de symétrie, révélant ainsi une transition de phase analogue à la transition par-ferromagnétique et la possible existence d’une « momentisation turbulente » (cf. aimantation spontanée à champ nul).
En conclusion, cet écoulement turbulent dans lequel nous pouvons avoir accès à la fois aux évolutions des états spatio-temporels et aux moyennes des grandeurs thermodynamiques apparait comme un outil parfaitement adapté à l'étude des transitions de phase hors équilibre dans les systèmes fortement fluctuants.
Références
P.-P. Cortet, A. Chiffaudel, F. Daviaud, and B. Dubrulle, Rev. Lett. 105, 214501 (2010) “Experimental Evidence of a Phase Transition in a Closed Turbulent Flow »
P-P Cortet, E Herbert, A Chiffaudel, F Daviaud, B Dubrulle and V Padilla, J. Stat. Mech. P07012 (2011), « Susceptibility divergence, phase transition and multistability of a highly turbulent closed flow ».