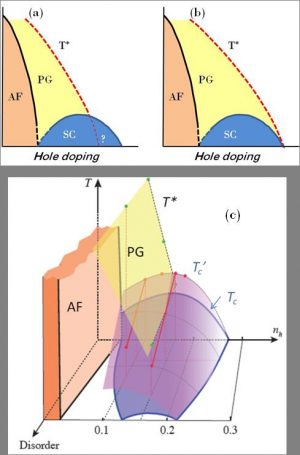
Après plus de 20 ans de recherche intensive, l’origine des hautes températures critiques observées dans les cuprates supraconducteurs n’est toujours pas élucidée. Une autre énigme de ces composés est la présence d’une phase dite de « pseudogap » caractérisée par l’ouverture partielle d’un gap dans les excitations de basse énergie au dessous d’une certaine température T*. Cette ligne de pseudogap, mise en évidence initialement par RMN [1], apparaît dans la région sous-dopée du diagramme de phase, c’est-à-dire pour des dopages inférieurs à celui où la température critique est maximale (voir figure 1). Si cette ligne de pseudogap est assez bien définie pour les faibles dopages, on trouve dans la littérature deux diagrammes de phase différents, suivant la façon dont elle se termine en fonction du système étudié et/ou de la technique expérimentale utilisée. Ces deux représentations sont reliées à des interprétations très différentes de l’origine du pseudogap. Dans le premier cas (1-a), la ligne de pseudogap atteint et/ou coupe le dôme supraconducteur au voisinage du dopage optimal et l’état pseudogap est considéré comme une phase différente, voire en compétition avec la supraconductivité ; dans le second (1-b), la phase de pseudogap enveloppe le dôme supraconducteur et est interprétée comme un état précurseur de l’état supraconducteur, les paires supraconductrices isolées se formant à T* alors que la cohérence de phase macroscopique entre les paires n’intervient qu’à la température critique de supraconduction Tc.
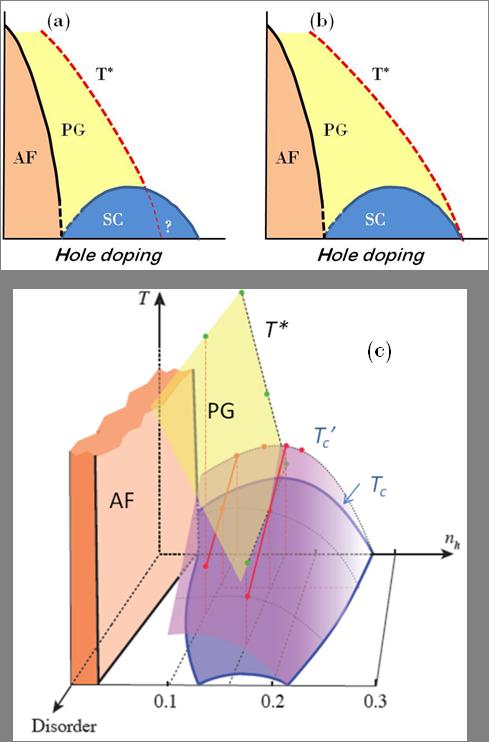
Figure 1 : (a) et (b) Diagrammes de phase schématiques proposés pour les cuprates à haute température critique. La ligne de pseudogap T* rejoint le dôme supraconducteur en (a) alors qu’il l’englobe en (b). (c) Diagramme de phase proposé en tenant compte du désordre. Les symboles représentent nos données expérimentales. La ligne T’c délimite le régime de fluctuations supraconductrices. Dans les échantillons purs, nous trouvons que T’c est supérieure à T* au voisinage du dopage optimal, montrant que le pseudogap ne peut pas être considéré comme un état précurseur de la supraconductivité. Sous l’’effet du désordre, le dôme supraconducteur se contracte, l’extension des FSC diminue légèrement alors que le pseudogap n’est pas modifié. On peut ainsi expliquer le schéma représenté en 1-b obtenu dans certains cuprates à bas Tc par des mesures spectroscopiques où la ligne T’c a été confondu avec celle du pseudogap.
Une façon de trancher entre ces deux interprétations est de déterminer à la fois l’extension des fluctuations supraconductrices (FSC) au dessus de Tc ainsi que la ligne de pseudogap au voisinage du dopage optimal. Expérimentalement, il est difficile de déterminer les FSC car il faut extraire la contribution supraconductrice d’un signal total provenant essentiellement de l’état normal qu’en général, on ne connaît pas. Dans les supraconducteurs à faible Tc, l’application d’un champ magnétique relativement faible permet de supprimer totalement l’état supraconducteur et donc de mesurer la contribution de l’état normal. Dans les cuprates supraconducteurs, les champs critiques supérieurs sont très élevés même au voisinage de Tc et ne sont pas accessibles avec les champs magnétiques disponibles actuellement.
Nous avions montré il y a quelques années qu’il était possible d’extraire la contribution des FSC à la conductivité électrique en mesurant la magnétorésistance en champ fort à des températures supérieures à Tc [2], et de déterminer très précisément la température T’c à laquelle cette contribution s’annule. Nous avons appliqué cette méthode plus récemment pour étudier les FSC dans différents cristaux de YBa2Cu3O7-δ en fonction du dopage en trous. La température T* du pseudogap pouvant être déduite de l’évolution en température de la résistivité, nous avons ainsi pu déterminer à la fois T* et T’c en utilisant la même sonde expérimentale [3,4].
Les mesures de magnétorésistance ont été effectuées en champ magnétique pulsé, jusqu’à 60 Tesla, au Laboratoire des Champs Magnétiques Intenses de Toulouse. Un exemple des courbes de magnétorésistance est reporté en fonction du carré du champ sur la figure 2. La partie hachurée sur la figure montre la contribution des fluctuations supraconductrices à la conductivité électrique qui peuvent être analysées quantitativement en fonction de la température et du champ magnétique.
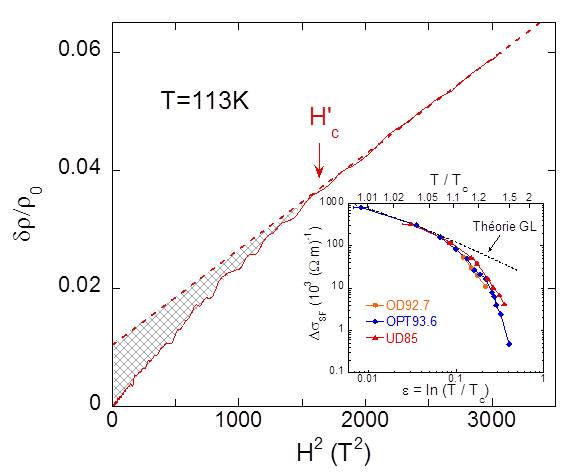
Figure 2 : Magnetorésistance δρ/ρ0=(ρ(H)-ρ(H=0))/ρ(H=0) mesurée sur un monocristal optimalement dopé de YBa2Cu3O7-δ(Tc = 93.5K). Dans l’état normal, la magnétorésistance est quadratique en champ (ligne en pointillés). Quand on diminue la température vers Tc, on observe des déviations par rapport à ce comportement au dessous d’un certain champ H’c. La partie grisée correspond à la contribution des fluctuations supraconductrices à la conductivité électrique. Remarquons qu’un champ H’c de ~40T est encore nécessaire à 113K, soit ~10K au dessus de Tc, pour tuer complètement les FSC.
L’analyse de cette contribution est reportée en fonction de la température réduite ε=Ln(T/Tc) dans l’insert pour différents cristaux caractérisés par leur position dans le diagramme de phase (OD= « overdoped », UD= »underdoped ») et leur Tc. Les données sont en bon accord avec l’approche Ginzburg-Landau des fluctuations supraconductrices tant que ε est inférieur à ~0.08.
Un résultat marquant de cette étude a été de montrer que l’on peut détecter des fluctuations supraconductrices au dessus de T* dans le composé optimalement dopé YBa2Cu3O7-δ [3], ce qui montre sans ambiguïté que le pseudogap ne peut pas être considéré comme un état précurseur de la supraconductivité et confirme donc le schéma reproduit sur la figure 1-a.
D’autre part, nous avons également montré que ce diagramme de phase pouvait être fortement modifié en présence de désordre introduit de façon contrôlée par irradiation aux électrons [5]. Notamment, on observe une augmentation significative du régime de FSC dans la région sous-dopée du diagramme de phase quand Tc est réduit par la présence de défauts. Ceci est illustré sur le diagramme général de la figure 1-c où l’effet du désordre a été rajouté sur un troisième axe. Ceci pourrait expliquer que, dans certains cuprates à bas Tc, la ligne marquant l’extrémité du régime de fluctuations ait pu être confondue avec la ligne de pseudogap, d’où le schéma de la figure 1-b.
Enfin l’analyse quantitative de l’évolution des fluctuations supraconductrices en température et en champ magnétique nous a permis de faire une détermination thermodynamique de certains paramètres microscopiques de l’état supraconducteur dans le cadre de la théorie de Ginzburg-Landau [4]. Nous avons en particulier trouvé que le gap supraconducteur extrait de cette analyse thermodynamique diminue quand on sous-dope le matériau, contrairement au pseudogap qui augmente, ce qui est une autre confirmation que la phase pseudogap est très différente de la phase supraconductrice des cuprates.
Références :
[1] H. Alloul, T. Ohno and P. Mendels, Phys. Rev. Lett. 100, 226802 (1989)
[2] F. Rullier-Albenque,H. Alloul, C. Proust, D. Colson and A. Forget , Phys. Rev. Lett. 99, 027003 (2007)
[3] F. Rullier-Albenque, H. Alloul, C. Proust, D. Colson and A. Forget , Europhys.Lett. 91, 37005 (2010)
[4] F. Rullier-Albenque,H. Alloul, G. Rikken, Phys. Rev. B 84, 014522 (2011)
[5] F. Rullier-Albenque, H. Alloul, R. Tourbot , Phys. Rev. Lett. 91, 047001 (2003)