En mesurant la conductance électrique g, on mesure la probabilité des électrons d’être transmis au travers du système mesuré. C’est la probabilité des électrons à l’énergie de Fermi EF que l’on mesure quand la température T→0. C’est la probabilité intégrée sur un intervalle d’énergie de largeur kB T autours de EF que l’on mesure quand T≠0. Pendant un temps h/(kB T) , les électrons parcourent une distance LT=vF h/(kB T) s’ils se déplacent balistiquement à la vitesse de Fermi vF. LT définit la longueur thermique.
Considérons une chaine (Fig. 1) incluant deux diffuseurs séparés d’une distance L. Quand on varie L , la transmission de cet interféromètre à EF (et donc sa conductance quand T→0) présente des oscillations de Fabry-Pérot de période égale à la moitié de la longueur d’onde de Fermi λF. Quand T≠0, l’intégrale de la transmission sur un intervalle d’énergie ~kBT autour de EF fait que ces oscillations disparaissent quand L excède LT. C’est la situation qui est habituelle en physique mésoscopique.
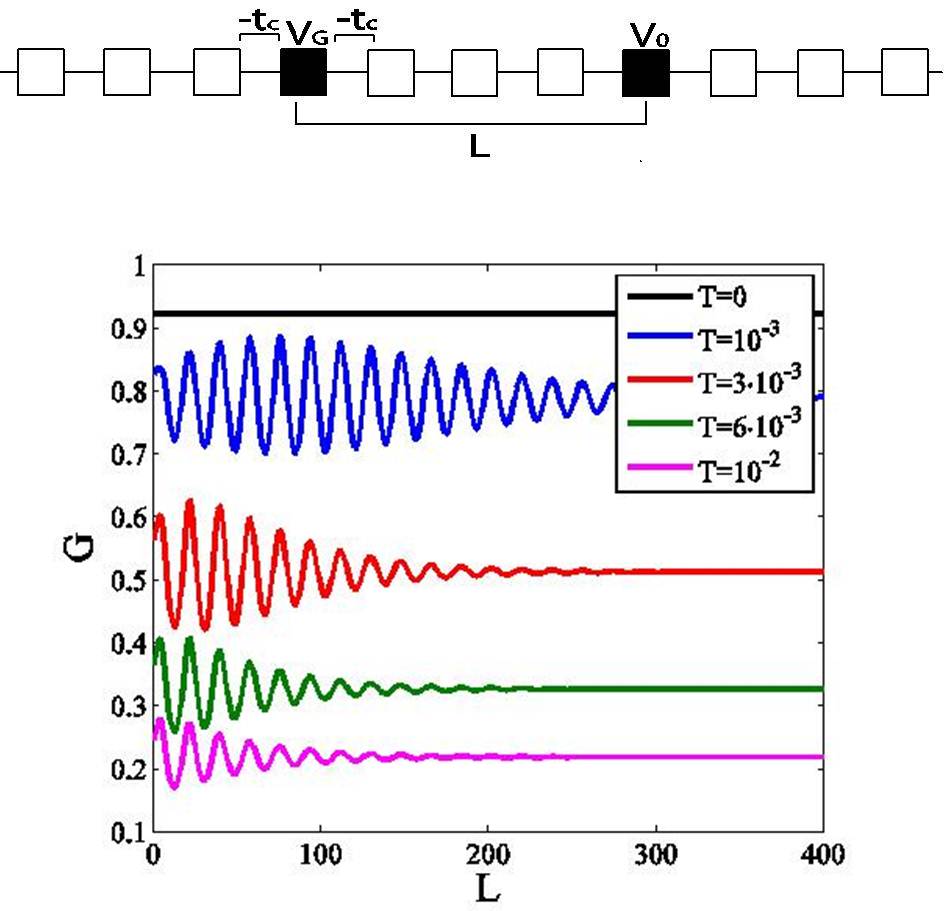
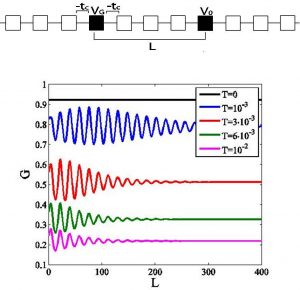
Fig 1 En haut : Un interféromètre 1d est engendré par 2 diffuseurs (potentiels VG et V0) séparés de L sites. Le site de potentiel Vg étant faiblement couplé par des termes de saut tc≪t (valeur des termes de saut entre les autres sites), le diffuseur de gauche a une transmission résonante de largeur Γ∝ tc 2 quand EF~VG.
En bas : Conductance g en fonction de la distance L à différentes températures T (en unité de t), quand le diffuseur de gauche est transparent à l’énergie de Fermi EF. La conductance est indépendante de L quand la température T→0 , mais oscille avec une période λF/2 quand T≠0.
Mais la situation se complique si l’un des 2 diffuseurs a une résonance de largeur Γ. Il devient alors possible d’ajuster la densité électronique de telle sorte que le diffuseur résonant soit totalement transparent à EF. Quand T→0 , l’interféromètre disparaît et sa conductance cesse d’osciller avec L ! C’est seulement si T≠0 que les électrons d’énergie E≠EF autour de la résonance contribuent au transport, que l’interféromètre réapparaît et que g oscille à nouveau avec une période λF/2 quand on fait varier L. Dans ce cas, nous dirons que l’interféromètre est induit thermiquement.
Une question se pose alors : jusqu’à quelle échelle peut-on observer les oscillations induites thermiquement ? Ce ne peut pas être LT, puisque les oscillations disparaissent quand LT→∞. Comme la résonance introduit une autre échelle d’énergie, sa largeur Γ , il est facile de deviner que l’échelle qui caractérise la décroissance des oscillations engendrées thermiquement doit être la longueur LΓ=(hvF )/Γ induite par la résonance, et non la longueur LT induite par la statistique de Fermi-Dirac. Une illustration d’oscillations 1d engendrées thermiquement est donnée en Fig.1.
Pour généraliser cette idée à 2d, prenons un modèle (Fig. 2) où deux réseaux carrés semi-infinis sont couplés via un seul site d’énergie VG par des éléments de saut tc. Ce contact donne lieu à une transmission résonante décrite par une forme de Breit-Wigner de largeur Γ∝tc2 . Un interféromètre est constitué en plaçant dans le demi-plan de droite un deuxième site de potentiel V0 qui diffuse les électrons transmis par le contact. La conductance g est donnée en Fig. 2 en fonction de la distance x entre le contact et le deuxième diffuseur, pour des valeurs croissantes de la température. Comme en Fig. 1. nous constatons que les oscillations de g(x) sont essentiellement induites par la température et deviennent négligeables quand T→0!
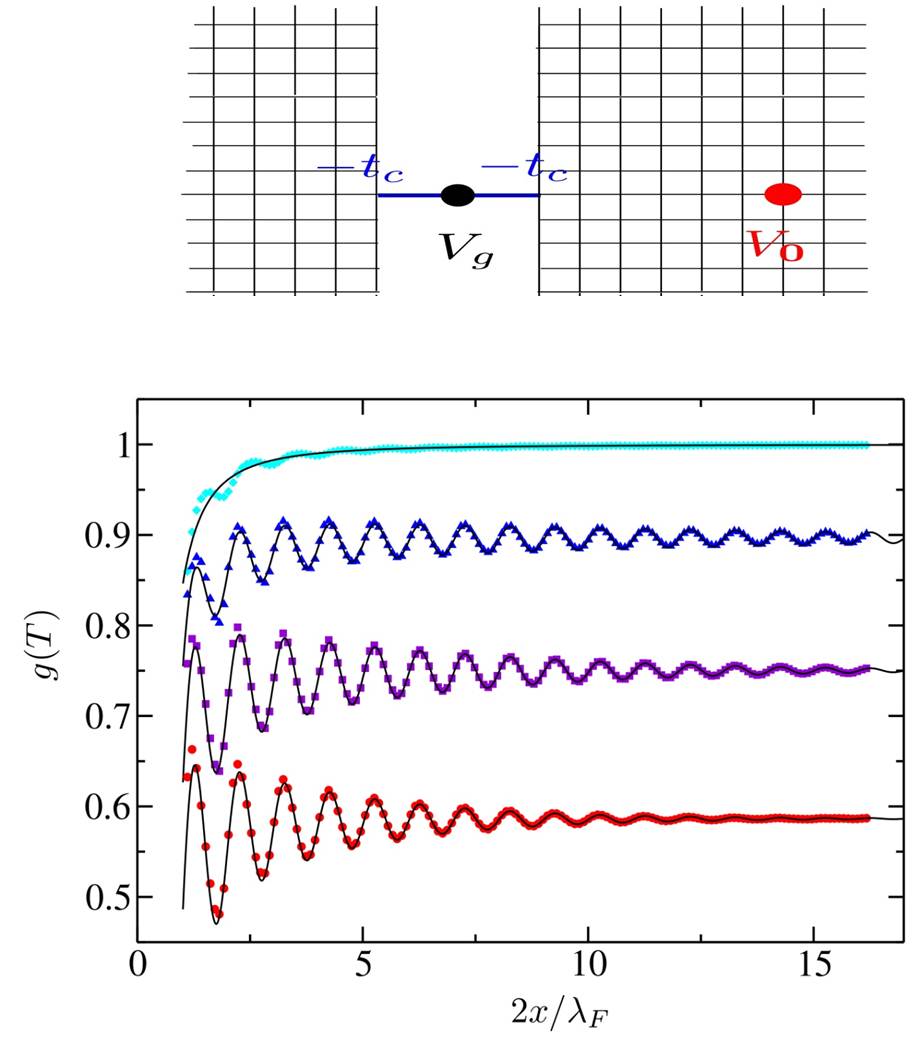
Fig.2. En haut : Le site de potentiel V_gest couplé ici à deux demi-plans par des termes de saut tc. Un diffuseur ( potentiel V0) est placé à une distance x du contact. En bas : Conductance g(2x/λF ) pour des températures croissantes (de haut en bas 2LT /λF=∞,9,4,2) quand le contact est ouvert à EF. Les franges d’interférence sont faibles quand T→0, croissent avec la température et persistent au dela de LT.
Prenons maintenant un modèle (Fig.3) où le contact n’est pas réduit à un seul site, mais à un très grand nombre de sites permettant de décrire un point selle couplant deux demi-plans dans la limite continue. En déplaçant un potentiel diffusant (tache rouge de coordonnées (x,y) dans la Fig.3) dans le demi-plan de droite, on obtient des images 2d donnant la différence g(x,y)-g0 entre les conductances avec (g) et sans ( g0) ce potentiel diffusant. L’image de gauche correspond à T→0, celle de droite à T≠0. Pour observer à nouveau des oscillations induites thermiquement, nous avons ouvert le contact aux bords du plateau où g0=e2/h quand T→0 (Fig.3-flèche verte). Nous montrons l’effet au bord du premier plateau, l’effet restant observable aux bords des autres plateaux.
La solution analytique du modèle donné en Fig.2 nous a permis de tirer les conclusions suivantes. (i) Les franges d’interférences sont peu visibles sur les plateaux, et très visibles entre les plateaux quand T→0. (ii) En se plaçant au bord d’un plateau, les franges observées sont essentiellement engendrées par la température, et peuvent persister sur des distances LΓ très supérieures à LT. (iii) Les franges sont données par des fonctions universelles de r/LΓ quand on fixe le rapport LT/LΓ, pour toute ouverture g0 du contact. (iv) La longueur LΓ est d’autant plus grande que l’ouverture des modes de conduction du contact est brutale (une petite variation de EF permettant d’ouvrir un nouveau mode). Ceci peut surprendre, mais s’explique facilement quand on réalise que l’ouverture d’un contact n’est rien d’autre qu’une forme de résonance.
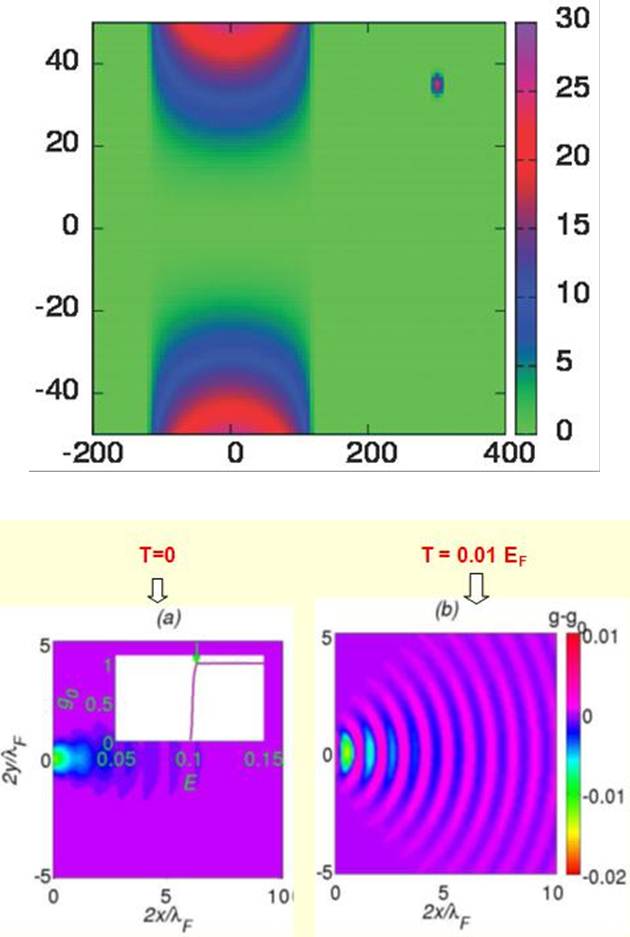
Fig.3 En haut : Le contact n’est plus réduit à un site, mais à 200×100 sites avec des potentiels indiqués par le code couleur (en unité de t=1). La tache rouge représente le deuxième diffuseur (« la pointe »).
En bas : Différence g-g0 entre les conductances avec et sans pointe, en fonction des coordonnées (x,y) de la pointe. La flèche verte indique la valeur g0 de la conductance sans la pointe quand T→0. Les franges sont faibles à gauche (T=0), alors qu’à droite, elles augmentent et persistent au dela de LT quand T~1 K (si EF~100 K).
En plus de leur intérêt théorique, ces résultats concernent des mesures faites d’abord à Harvard il y a plus de 10 ans: l’étude par microscope à effet de grille d’un contact quantique ponctuel. Le principe en est décrit en Fig.4. Cette microscopie par effet de grille permet d’étudier de façon exceptionnelle le transport quantique dans les nanostructures. Son étude a fait l’objet de 2 projets soutenus par l’ANR. ITEM-Th réunit des théoriciens du CEA Saclay et de l’IPCMS-Strasbourg. ITEM-Exp regroupe des expérimentateurs de l’institut Néel et du CEA à Grenoble, les systèmes étudiés étant fabriqués au LPN de Marcoussis. Au SPEC, la théorie de la microscopie par effet de grille de contacts quantiques a fait l’objet des thèses d’Axel Freyn (effet des interactions dans le contact) et d’Adel Abbout (effet de la température), ainsi que des post-docs de Gabriel Lemarié (calcul des fonctions d’échelle) et d’Andrii Kleshchonok (effet des interactions et de la température).
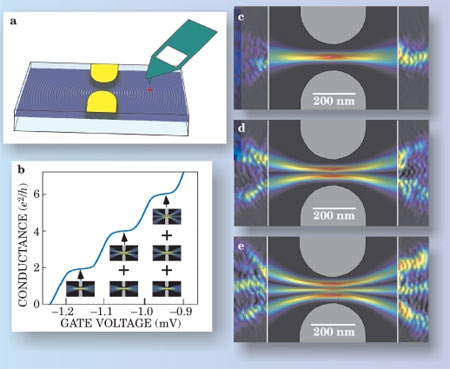
Fig. 4 Microscopie à effet de grille d’un contact quantique ponctuel : (a) Un gaz d’électrons 2d (bleu) est créé dans une hétérostructure semiconductrice. Des grilles (jaune) forment un contact au milieu. La pointe chargée (vert) d’un microscope AFM engendre une zone de dépletion (rouge) dans le gaz 2d. (b) En variant la tension sur les grilles, on ouvre les canaux de conduction du contact. En ouvrant un nouveau canal, la conductance saute de 2 e2/h. (d) Conductance (extremités des figures) de l’interferomètre en fonction de la position de la pointe quand le contact à un canal (c), 2 canaux (d) ou 3 canaux d’ouvert (e). Les ouvertures sont données par les flêches en (b)).
(d'après M. Topinka, R. Westervelt et E. Heller, Physics Today 56, 47 (2003))
Pour en savoir plus, trois références obtenues dans le cadre du projet ANR Item-Th.
[1] « Scanning Gate Microscopy of a Nanostructure Where Electrons Interact », Axel Freyn, Ioannis Kleftogiannis et Jean-Louis Pichard, Phys. Rev. Lett. 100, 226802 (2008)
[2]«What is Measured in the Scanning Gate Microscopy of a Quantum Point Contact? », Rodolfo A. Jalabert, Wojciech Szewc, Steven Tomsovic, et Dietmar Weinmann, Phys. Rev. Lett. 105, 166802 (2010)
[3] « Thermal Enhancement of Interference Effects in Quantum Point Contacts », Adel Abbout, Gabriel Lemarié et Jean-Louis Pichard, Phys. Rev. Lett. 106, 156810 (2011)