Le problème de la transition vitreuse est selon le prix Nobel de Physique P.W. Anderson le « problème le plus profond et le plus intéressant en physique de l'état condensé ». A première vue pourtant, il est difficile de penser que des matériaux aussi courants que les verres puissent encore constituer un « mystère » de la physique. De fait, les verres représentent l'archétype de ce que l'on appelle aujourd'hui les « systèmes complexes ». Leur complexité est associée à un effet de « frustration » : l'existence de contraintes antagonistes empêche les particules (atomes, molécules) d'évoluer vers une configuration d’énergie minimale par une simple optimisation des structures locales. Cet effet est présent dans beaucoup d’autres situations, comme dans les colloïdes, ou dans la matière granulaire, ou encore pour des domaines plus abstraits comme l'informatique, la théorie des jeux ou l'optimisation combinatoire.
Un verre est obtenu à partir d'un liquide refroidi suffisamment vite pour qu’il ne cristallise pas et qu’il reste dans un état métastable appelé liquide surfondu. Si à partir de cet état on baisse encore la température, le temps de relaxation τ augmente extrêmement vite, jusqu'à dépasser les temps expérimentaux typiques en dessous de la température de transition vitreuse Tg. Ce passage de l'état liquide au verre échappe pour l’instant aux théories des transitions de phase qui ont pourtant décrit avec succès de nombreux phénomènes physiques, comme la transition liquide-gaz ou paramagnétique-ferromagnétique. L'existence même d'un état vitreux bien défini et par conséquent d'une vraie transition vitreuse thermodynamique est toujours en débat; il pourrait plutôt s'agir d'une transition entre deux régimes dynamiques différents.
Dans les nombreux scénarios envisagés pour la transition vitreuse, une idée centrale est que l’évolution du système n’est permise que si dans certaines régions de l’espace, les particules « coopèrent » pour réorganiser leur structure (hétérogénéités dynamiques). Cette idée permet d’expliquer l’augmentation brutale du temps de relaxation τ lorsque la température tend vers Tg. D’un point de vue expérimental, il est de plus en plus clair que la dynamique à l'approche de la phase vitreuse est très hétérogène : des régions lentes coexistent avec des régions rapides. Ce caractère hétérogène est associé à la nécessité de réorganiser collectivement des régions entières. Le ralentissement est alors associé à la croissance d'une longueur de corrélation dynamique, observée de façon précise dans des simulations numériques, mais seulement de manière très indirecte expérimentalement.
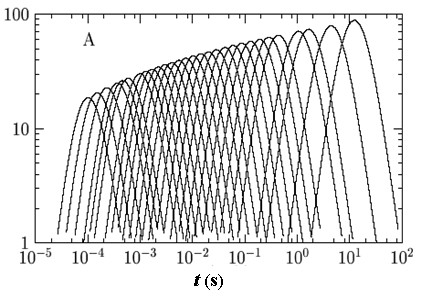
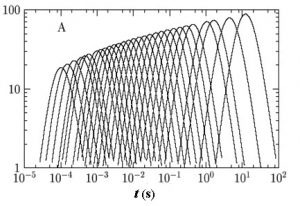
L’accès direct à cette longueur de corrélation dynamique dans les verres en formation en fonction de la température ou de la densité est donc un enjeu majeur. Avec l’Institut de Physique Théorique (CEA/IPhT) et le Laboratoire des Colloïdes, Verres et Nanomatériaux (LCVN, Montpellier II), nous avons proposé et mis en œuvre expérimentalement une méthode simple permettant d’estimer cette longueur. Cette méthode utilise une généralisation des relations fluctuation-dissipation (qui remontent, dans leur forme la plus simple, à l’article d’Einstein de 1905 sur le mouvement Brownien) pour relier la dépendance en température d’observables facilement accessibles, comme la constante diélectrique ou le facteur de structure dynamique à la taille typique des hétérogénéités dynamiques. Des expériences mettant en œuvre ces idées – sur le glycérol dans notre groupe, et sur un système colloïdal au LCVN de Montpellier – nous ont permis d’obtenir la première confirmation expérimentale qu’une longueur de corrélation dynamique croît bien à l’approche la transition vitreuse, et d’estimer cette longueur quantitativement. Un exemple de nos résultats expérimentaux est reproduit dans la figure ci-dessous: chaque courbe correspond à une mesure effectuée sur le glycérol à une température donnée, T = 232K, 231K,…, 192K de gauche à droite (Tg =190K), et montre, en ordonnée, le nombre de particules qui doivent bouger de façon concertée au temps t afin de permettre au système de passer d’une configuration microscopique à une autre.
Une extension de cette méthode à une plus grande gamme de fréquence, à d’autres matériaux (comme les verres de spin) et en dessous de la température de transition vitreuse, devrait permettre de départager les nombreux scénarios théoriques proposés au cours des quarante dernières années pour décrire la dynamique anormalement lente des verres, et de soulever un coin du voile qui recouvre l’un des grands « mystères » de la physique statistique.
L. Berthier, G. Biroli, J.-P. Bouchaud, L. Cipelletti, D. El Masri, D. L’Hote, F. Ladieu, M. Pierno, Science, 310, 1797, (2005).
C. Dalle-Ferrier, C. Thibierge, C. Alba-Simionesco, L. Berthier, G. Biroli, J.-P. Bouchaud, F. Ladieu, D. L’Hôte, and G. Tarjus, Phys. Rev. E 76, 041510 (2007).