Quand les conducteurs bruyants émettent de la lumière

La tension aux bornes d’un conducteur à l’équilibre présente des fluctuations proportionnelles à la température et à la résistance de ce conducteur. On parle dans ce cas de bruit thermique, ou encore bruit Jonhson-Nyquist. Lorsque le conducteur est couplé à des guides d’ondes coaxiaux, les fluctuations génèrent des photons dont la statistique à l’équilibre est une statistique chaotique similaire au rayonnement d’un corps noir. Lorsque que le conducteur est porté hors équilibre, l’aspect stochastique du transport électronique donne lieu à des fluctuations de courants (le bruit de grenaille) menant à une statistique de photons émis plus compliquée. Ce problème a donné lieu à de nombreuses études théoriques qui prédisent une statistique de phonons allant du chaos à un comportement non-classique [1].

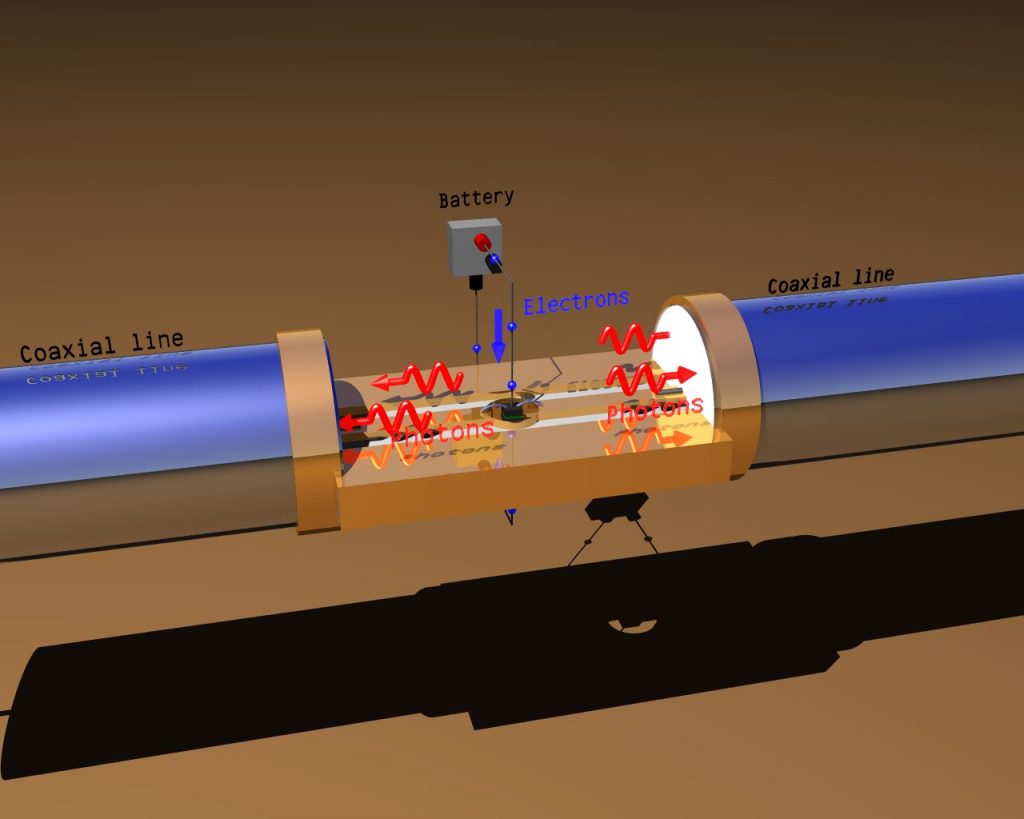
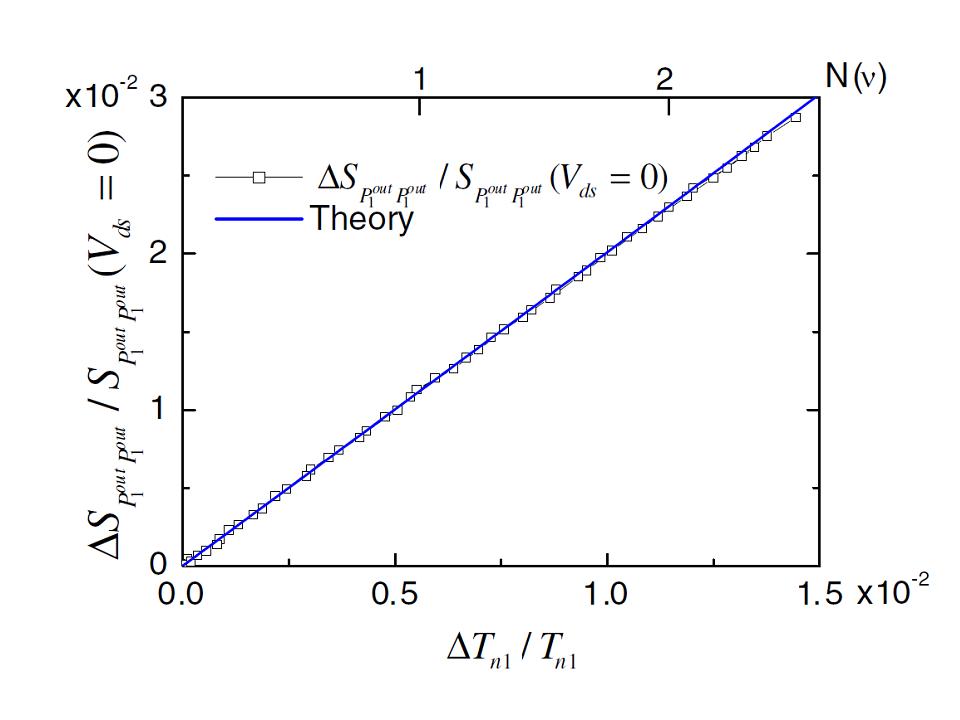
Pour apporter des réponses aux questions posées sur cette physique nouvelle, établissant un pont entre l’optique quantique et les conducteurs quantiques, l’équipe Nanoélectronique du SPEC a étudié la statistique des photons microondes émis par une jonction tunnel à basse température. Ils ont étudié les corrélations entre photons (et par conséquent leur statistique) par interférométrie Hanbury Brown-Twiss(figure 1), méthode utilisée dans les années cinquante en astronomie pour étudier la taille des étoiles. L’équipe du SPEC a montré que les photons émis par une jonction tunnel présentent une statistique chaotique, même lorsque le taux d’émission de photons est de l’ordre de l’unité. Ce travail est une étape importante vers l’étude de la statistique des photons émis par un conducteur monomode, pour lequel les théories prédisent un rayonnement sous-Poissonien[Figure 2].

---