H. Cao, A. Gukasov, I. Mirebeau, P. Bonville, C. Decorse, and G. Dhalenne
Dans les composés magnétiques géométriquement frustrés, l’état fondamental résulte d’un équilibre subtil entre différents termes d’énergie. Des ordres magnétiques exotiques à courte portée, comme les glaces de spin ou les liquides de spin, peuvent être stabilisés, sans désordre chimique. Leur étude stimule actuellement beaucoup de travaux expérimentaux et théoriques.
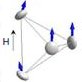
Un réseau cristallin où la frustration joue un rôle important est le réseau pyrochlore. Dans les pyrochlores de formule R2Ti2O7, les ions magnétiques de terre rare R3+ sont situés sur des tétraèdres jointifs par les sommets. La symétrie locale du site R est ternaire, relative à l’axe d’anisotropie <111> qui joint un sommet du tétraèdre à son centre. En présence d’un champ magnétique, l’orientation et la valeur du moment magnétique de chaque terre rare résulte d’un compromis entre l’énergie Zeeman associée au champ appliqué et celle du champ électrique cristallin, qui impose une anisotropie soit parallèle, soit perpendiculaire à l’axe local.
Comment mesurer la susceptibilité locale? La difficulté vient du fait que les 4 sommets d’un tétraèdre ont chacun un axe local <111> différent : la susceptibilité macroscopique, mesurée avec un magnétomètre, correspond donc à une moyenne sur les 4 axes, même lorsque l’échantillon est monocristallin. L’idée est de mesurer la susceptibilité par diffraction de neutrons polarisés, ce qui augmente la sensibilité lorsque les moments induits sont faibles (petit champ magnétique, haute température). La relation entre le moment et le champ appliqué est décrite par un tenseur de susceptibilité qui, par raison de symétrie, ne possède que deux composantes Χ// et χ⊥. L’affinement simultané de centaines de pics de diffraction permet de déterminer ces grandeurs à chaque température, indépendamment de la direction du champ.
Des mesures effectuées sur 4 composés (R=Ho, Tb, Yb, Er) ont mis en évidence une anisotropie soit planaire (Er, Yb), soit axiale (Tb, Ho). L’essentiel de la variation thermique de la susceptibilité s’explique par le peuplement progressif des niveaux de champ cristallin, dont l’espacement a été déterminé indépendamment par diffusion inélastique de neutrons. Pour expliquer complètement la susceptibilité mesurée, il faut introduire dans un modèle de champ moléculaire, une interaction d’échange et /ou dipolaire. De façon surprenante, c’est aussi une grandeur tensorielle, c’est-à-dire anisotrope. Encore plus surprenant, dans les deux cas (Er et Yb) que nous montrons, l’anisotropie semble provenir non pas du couplage dipolaire, ce qui est classique, mais de l’échange, ce qui l’est beaucoup moins. Un nouvel élément à prendre en compte dans la théorie !
Susceptibilité locale de Er2Ti2O7 (XY, AF) et Yb2Ti2O7 (XY, F) déduites de mesures de neutrons polarisés en phase paramagnétique; les lignes en pointillés représentent le calcul de champ cristallin seul, les lignes continues le calcul auto-consistent avec champ moléculaire.
Contacts : A. Gukasov, I. Mirebeau (LLB) ; P. Bonville (SPEC)
Référence :
H. Cao,1 A. Gukasov,1 I. Mirebeau,1 P. Bonville,2 C. Decorse,3 and G. Dhalenne3
Phys. Rev. Lett. 103, 056402, (2009).
1Laboratoire Léon Brillouin, CEA-CNRS, CE-Saclay, 91191 Gif-sur-Yvette, France
2Service de Physique de l’Etat Condensé, CEA-CNRS, CE-Saclay, 91191 Gif-Sur-Yvette, France
3Laboratoire de Physico-Chimie de l’Etat Solide, ICMMO, Université Paris-Sud, 91405 Orsay, France