Un nouvel état de la matière dans votre ordinateur ?

(

On pensait bien connaitre la physique des transistors, et en particulier celle de ceux qui peuplent par millions le cœur de nos ordinateurs, les MOSFETs au Silicium (Metal Oxyde Semi-conducteur Field Effect Transistor). Or, dès 1994 une nouvelle génération de MOSFETs à très haute mobilité a permis de réaliser des expériences où la densité électronique était extrêmement basse (Kravchenko et al 1994). Les expériences menées dans ces « transistors extrêmes » ont montré un comportement tout à fait spectaculaire : à basse température ils se comportent comme des métaux au lieu de l’isolant attendu. (Au lieu de diverger, la résistivité décroit d’un ordre de grandeur dans une fenêtre de température assez étroite).

Pas de métaux à 2 dimensions.

Pour comprendre l’émoi que ces résultats expérimentaux ont suscité dans la communauté, il faut remonter au célèbre article sur la localisation pour lequel P.W. Anderson a obtenu son prix Nobel en 1977 (voir article : Anderson 1958). Anderson y étudie l’effet d’un faible désordre dans les métaux et conclut qu’à très basse température (i.e. pour un système quantiquement cohérent) les interférences multiples générées par ce désordre provoquaient une localisation des fonctions d’onde du métal, le rendant ainsi isolant. L’effet est particulièrement fort à une et deux dimensions (comme dans nos MOSFETs) où il était prédit qu’un petit désordre, même arbitrairement faible, suffisait à rendre le système isolant. Pendant deux décennies, la communauté a vérifié à la fois expérimentalement et théoriquement ce paradigme : pas de métaux à deux dimensions. En particulier le SPEC, à travers notamment les travaux de M. Sanquer et de J-L Pichard, a fortement contribué à l’étude de la localisation.

Le suspect idéal, les corrélations électroniques. Les expériences de Kravchenko, reproduites ensuite dans divers groupes expérimentaux (au SPEC également, dans le groupe de D. L’Hôte) ont ainsi été à l’origine d’une petite révolution dans la communauté du transport quantique. Les modèles et mécanismes affluèrent de toutes parts pour tenter de résoudre le fâcheux différent entre la théorie et les mesures expérimentales qui persistaient à montrer un comportement métallique. Les uns cherchaient des artefacts expérimentaux tandis que les autres proposaient des modèles plus ou moins farfelus ou ad hoc. Sur un seul point un consensus émergeait : à très basse densité, les corrélations électron-électron introduites par la répulsion Coulombienne prennent une importance considérable. Or ces corrélations résistent à la plupart des approches théoriques.

Localisation et Corrélations.

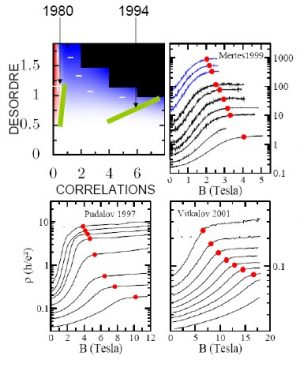
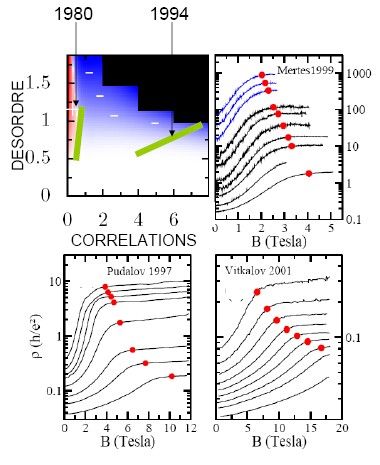
Dans le cadre de la thèse de Geneviève Fleury, nous avons développé une approche numérique, alliant Monte-Carlo quantique pour traiter le problème quantique à N corps et théorie d’échelle pour extraire la limite thermodynamique. Cette approche nous a permis, pour la première fois, d’étudier le problème couplé de la localisation d’Anderson en présence de corrélations fortes. Le diagramme de phase obtenu (voir figure) montre bien la « phase »métallique dans la région expérimentale où elle a été observée, et ce, ab initio (i.e. sans paramètre ajustable). Le scénario qui se dégage de nos calculs est en demi-teinte : d’un coté les corrélations sont bien à l’origine des observations expérimentales – une physique nouvelle émerge des corrélations. De l’autre le système reste un isolant au sens thermodynamique du terme. Autrement dit, nous prédisons qu’à plus basse température la résistivité doit diverger en accord avec le paradigme d’Anderson.

En haut à gauche : diagramme de phase obtenu. La région blanche correspond au régime diffusif, la région rouge au régime isolant et la région bleue à un « métal » apparent. Les expériences des années 80 étaient situées dans le rouge alors que celles de Kravchenko 1994 explorent la région bleue. En bas et à droite : les trois courbes montrent des exemples de magnétorésistances pour 3 expériences différentes. Les points rouges correspondent aux champs magnétiques où nous prédisons la saturation de la résistivité, en excellent accord avec les observations expérimentales. En tout, huit jeux de courbes ont été analysés et montrent un accord quantitatif avec nos résultats ab-initio, tant pour les magnétorésistances que pour les dépendances en température. Le diagramme de phase correspond à quelques dizaines d’années de calcul sur un processeur récent.

References:

[1] P. W. Anderson, Phys. Rev. 109, 1492 (1958)

[2] S. V. Kravchenko, G. V. Kravchenko, J. E. Furneaux, V. M. Pudalov, and M. D’Iorio, Phys. Rev. B 50, 8039 (1994

[3] J.-L. Pichard and G. Sarma, J. Phys. C 14, L127 (1981)

[4] Jean-Louis Pichard, Marc Sanquer, Keith Slevin, and Philippe Debray Phys. Rev. Lett. 65, 1812 (1990)

[5] R. Leturcq, D. L’Hôte, R. Tourbot, C. J. Mellor, and M. Henini, Phys. Rev. Lett. 90, 076402 (2003), http://fr.arxiv.org/abs/0902.3171

[6] G. Fleury and Xavier Waintal, http://fr.arxiv.org/find/cond-mat/1/au:+Fleury_G/0/1/0/all/0/1

[7] G. Fleury and X. Waintal, Phys. Rev. Lett. 101, 226803 (2008)

[8] G. Fleury and X. Waintal, Phys. Rev. Lett. 100, 076602 (2008)

Contacts : Geneviève Fleury et Xavier Waintal