La spectroscopie de résonance magnétique nucléaire (RMN) permet d’obtenir des informations sur la composition chimique des solides. Elle nécessite usuellement un grand nombre de spins nucléaires identiques pour obtenir un signal suffisant, ce qui restreint son application à des systèmes homogènes. Après avoir pu détecter un spin électronique unique, l’équipe Quantronique du SPEC a développé une méthode permettant la spectroscopie RMN de spins nucléaires individuels dans des solides.
Pour cela, un spin électronique, porté par un ion au sein d’un cristal refroidi à 10 mK, est utilisé comme antenne pour détecter les spins nucléaires qui l’entourent. Ce spin électronique est détecté par Spectroscopie de Résonance Paramagnétique Électronique (RPE), au moyen d’une méthode de comptage de photons micro-ondes, récemment développée par l’équipe. Le champ magnétique vu par ce spin dépend de l’état (« up » ou « down ») des spins nucléaires qui l’environnent, état que l’on peut identifier via la fréquence de résonance observée (entre états de structure hyperfine). Ces travaux ouvrent la voie à l’utilisation de spins nucléaires individuels pour le calcul quantique, et à la spectroscopie RMN de molécules individuelles.
Effectuer la spectroscopie RMN d’objets individuels, et tout particulièrement de molécules, a été un rêve du domaine depuis sa création. Cette sensibilité ultime permettrait d’accroître la résolution en éliminant l’inhomogénéité spectrale, et autoriserait l’analyse de systèmes aux propriétés hétérogènes, pour lesquels la résonance magnétique ne peut être appliquée. Ce rêve est rendu très difficile par la faiblesse du signal généré par un spin nucléaire, qui rend sa détection directe impossible. La seule méthode démontrée consiste à utiliser un spin électronique pour sonder les spins nucléaires environnants par interaction hyperfine, mais il faut alors détecter ce spin électronique individuel. Pour un tout petit nombre de types de spins électroniques, c’est possible par détection optique ou électrique, mais la grande majorité des spins électroniques ne peuvent pas être mesurés ainsi.
En 2023, une nouvelle méthode de détection de spins électroniques individuels par comptage de photons micro-ondes à 10 mK [1,2] a été mise au point au laboratoire. Cette méthode est particulièrement intéressante car elle est en principe applicable à n’importe quel spin électronique. Dans ce nouveau travail [3], il est montré que cette méthode permet aussi la détection de spins nucléaires individuels entourant le spin électronique. Ce résultat est obtenu dans un cristal de scheelite de formule chimique CaWO4, sur des ions Er3+ qui se comportent comme des spins électroniques à basse température [2] (figure a, b). Ce spin électronique est excité depuis son état fondamental ↓ vers son état excité ↑ par une impulsion micro-onde, après quoi il relaxe vers ↓ par émission d’un photon à la fréquence de transition ωs entre ces deux niveaux, qui est par la suite détecté par un compteur de photon micro-onde basé sur un qubit supraconducteur [4]. La grande majorité des atomes d’oxygène et de calcium n’ayant pas de spin nucléaire, c’est le tungstène qui fournit des spins nucléaires autour de chaque ion Er3+, par son isotope 183W (abondance naturelle de 14%) qui possède un spin nucléaire ½.
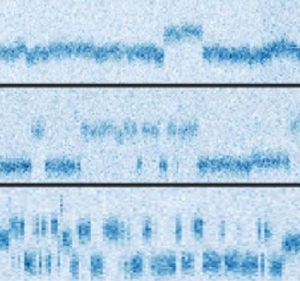
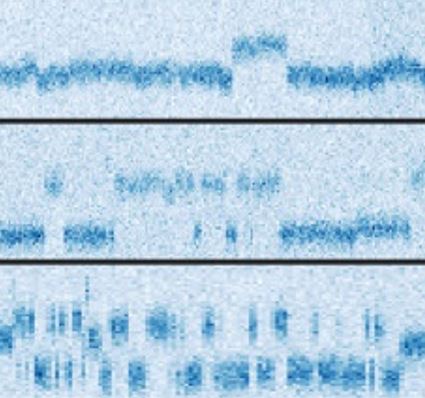
Dans une première étape, les sous-niveaux électroniques des atomes d’Er3+ sont séparés, avec l’application d’un champ magnétique, par effet Zeeman. L’écart précis en énergie entre niveaux est fonction des détails de l’environnement de chaque ion. Par spectroscopie, il devient alors possible d’ajuster le champ externe, pour accorder la fréquence de transition entre ces niveaux pour un atome individuel avec celle d’un résonateur de détection, utilisé pour exalter la relaxation radiative par effet Purcell de spin [5]. Suite à une impulsion micro-onde d’excitation dont on fait varier la fréquence ω, on mesure le nombre C(ω) de photons micro-ondes ré-émis, qui présente un excès lorsque ω est résonant avec la fréquence ωS du spin d’Er3+. Cette mesure de C(ω) est répétée pendant 150 minutes.
Pour certains atomes, on observe que ωS change soudainement et de manière répétée.
Chaque saut est la signature du changement d’orientation du spin nucléaire d’un atome de 183W voisin. L’écart en fréquence donne directement la valeur du couplage hyperfin A entre le spin de 183W et celui d’Er3+ (figure d). L’observation de ces sauts quantiques est une preuve directe qu’il s’agit de spins nucléaires individuels, puisque chaque atome d’Er3+ a une configuration de 183W différente autour de lui, du fait du caractère probabiliste de l’occupation de chaque site cristallin du tungstène par cet isotope.
En mesurant le nombre de coups C(ω) obtenus après excitation de l’atome d’Er3+ à l’une de ces deux fréquences (ω = ωS ± A/2), on obtient une lecture en un coup de l’état du spin nucléaire de 183W (figure e). On peut alors procéder à la spectroscopie de ce spin, dans le but de mesurer sa fréquence de résonance ωI. Pour cela, on cherche à exciter des transitions dites interdites (mais faiblement autorisées), où le spin électronique et le spin nucléaire changent simultanément d’état, pour les fréquences ωS ± ωI (figure d). Le spin nucléaire de 183W est préparé dans l’état ⇓ (voir paragraphe suivant), puis une impulsion d’excitation micro-onde à ωS + δ est appliquée, suivie de la mesure de l’état du spin nucléaire. La figure (f) montre la probabilité que le spin reste à l’état ⇓ (absence de transition) en fonction de δ. Une résonance est observée pour ωI /2π = -785 kHz. On vérifie ainsi que le rapport gyromagnétique ωI/B0 correspond bien à la valeur connue de 1.774MHz/T, pour un atome de 183W.
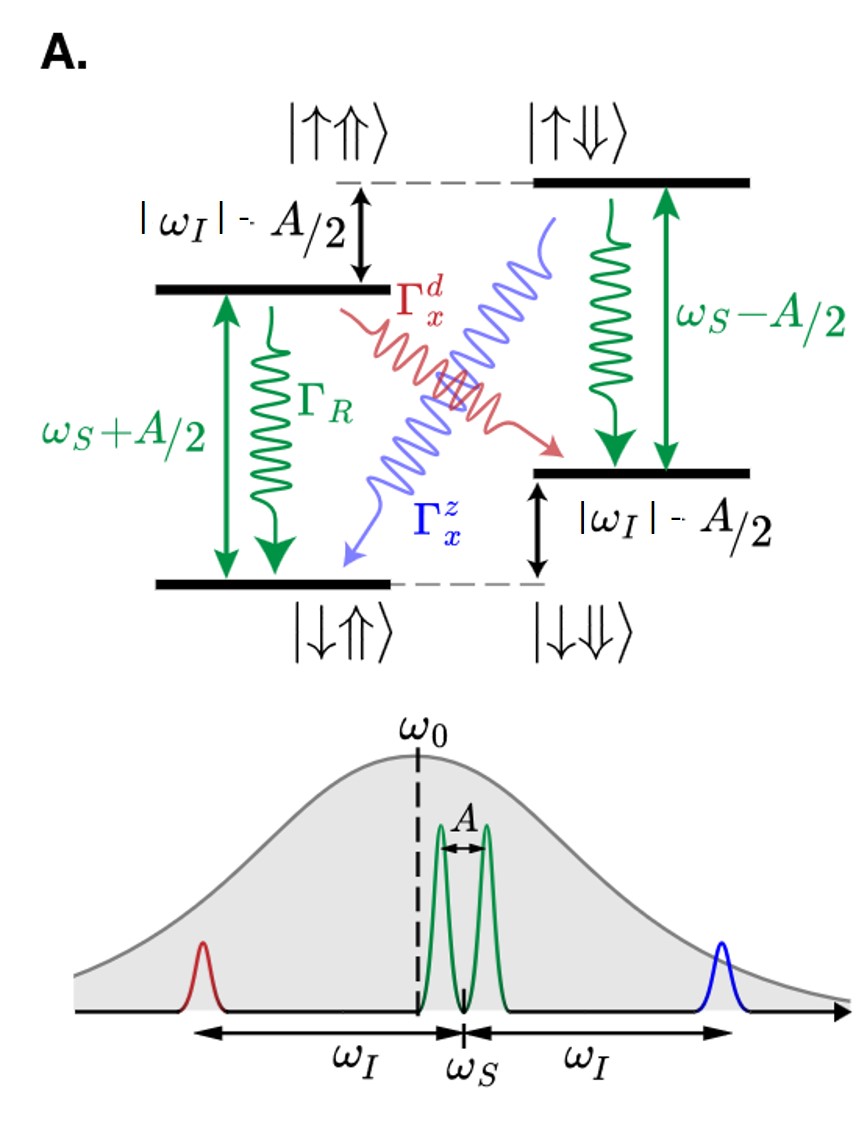
Figure 1 : En haut : Schéma des niveaux hyperfins de l’atome d’Er3+ en présence d’un atome 183W adjacent porteur d’un spin nucléaire, et les différentes transitions entre niveaux : en vert, les transitions dipolaires magnétiques permises, avec retournement du spin électronique ↓ → ↑ et sans retournement du spin nucléaire (⇓ (⇑) → ⇓(⇑)). En rouge et violet les transitions « interdites », avec retournement du spin nucléaire de 183W.
En bas : spectroscopie des niveaux et les différentes fréquences utilisées.
Pour finir, les transitions interdites peuvent être utilisées pour polariser un ou plusieurs spins nucléaires autour de l’atome d’Er3+ de manière déterministe dans leur état de plus basse (⇑) ou de plus haute (⇓) énergie. Pour ceci, on préparer le spin nucléaire de 183W dans l’état ⇑ en appliquant 10 impulsions à la fréquence ωS + ωI suivi de l’application répétée d’impulsions micro-ondes à la fréquence ωS – ωI . Si le spin nucléaire est dans l’état ⇓, rien ne peut se passer car aucun niveau n’est accessible depuis |↓ ⇓> à cette fréquence. L’état |↓ ⇑> peut en revanche être excité vers l’état |↑ ⇓>, suivi d’une relaxation vers |↓ ⇓> avec une forte probabilité. Au bilan, la probabilité totale de trouver le spin nucléaire dans l’état ⇓ a augmenté. L’application de plusieurs impulsions, séparées du temps nécessaire à la relaxation, permet de à préparer l’état ⇓ avec une grande probabilité. Cet effet est démontré à la figure (g), où une probabilité de 0.8 est atteinte après quelques impulsions. Cette technique de polarisation dynamique nucléaire par effet solide a été découverte par Abragam en 1958 [6] ; elle est ici appliquée avec succès à des spins nucléaires individuels.
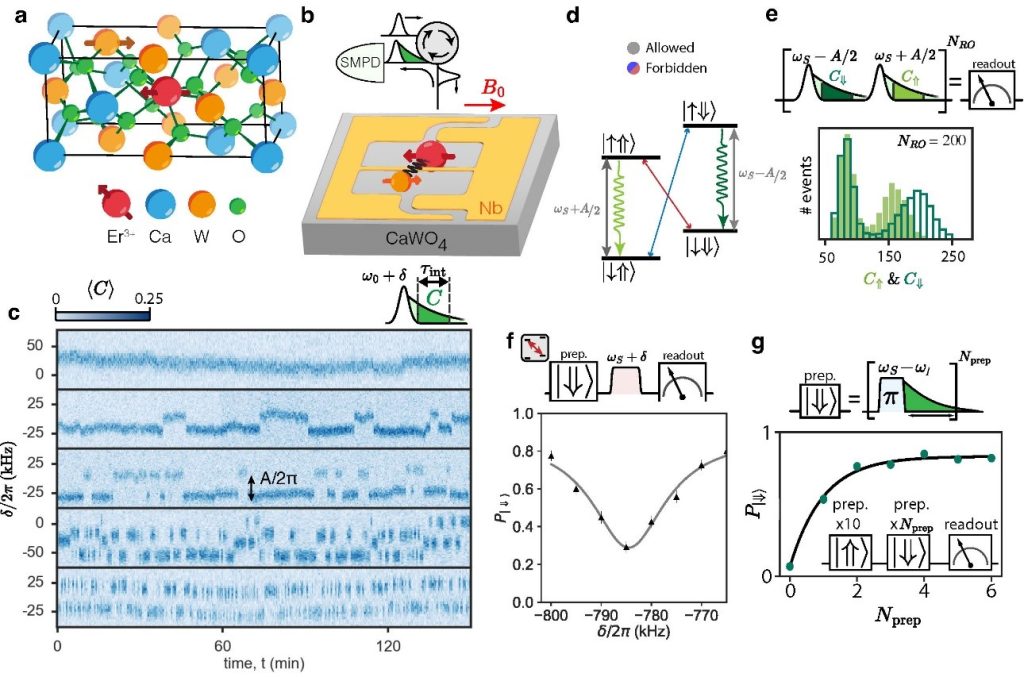
Figure 2 : Principe détaillé de l’expérience
(a) Maille élémentaire de CaWO4 : au centre de la maille, un ion Er3+ (rouge), en substitution de Ca2+, se comporte comme possédant un spin électronique S=1/2 (flèche rouge). Un atome adjacent de W (orange) peut être l’isotope 183W (abondance 14%), qui possède un spin nucléaire I=1/2 (flèche).
(b) L’ion Er3+ est placé dans un champ magnétique B0 ajustable qui permet d’accorder sa fréquence de transition ωS entre niveaux Zeeman hyperfins, à la fréquence de résonance ω0 d’un résonateur micro-onde supraconducteur (en jaune), auquel il est couplé magnétiquement. L’ion excité à cette fréquence ωS relaxe en émettant un photon micro-onde, détecté par un compteur de photons micro-ondes individuels.
(c) Sauts quantiques de spins nucléaires individuels de 183W. Mesure pour 5 ions Er3+distincts du nombre de photons <C(ω)> détectés par unité de temps d’intégration (code couleur) en fonction de l’écart δ = ωs – ω0 entre la fréquence d’excitation et celle du résonateur. La mesure est répétée pendant 150 minutes. Pour 4 de ces atomes, δ présente des sauts quantiques, d’amplitude A, signature de l’inversion du spin nucléaire de 183W.
(d) Schéma des niveaux électroniques hyperfins du système de spin couplé Er3+–183W. L’état fondamental (excité en spin) de Er3+ est noté ↑ (↓) et ceux de 183W : ⇓ (⇑). Les deux transitions dipolaires magnétiques conservant l’état du spin nucléaire (flèches verticales grises) sont autorisées et présentent un écart en fréquence A. Les transitions où le spin électronique de Er3+ et le spin nucléaire de 183W sont simultanément inversés (flèches bleues et rouges) sont « interdites », ou faiblement autorisées, et peuvent être excitées par des impulsions micro-ondes aux fréquences ωs ± ωI.
(e) Lecture en un coup du spin nucléaire : après excitation répétée (NR0 = 200 fois) des transitions autorisées (spin nucléaire de 183W invariant ⇑ ou ⇓) Les histogrammes de C⇓ et C⇑ sont bivalués.
(f) Spectroscopie de transition interdite. Le 183W est initialement préparé dans l’état ⇓, avant l’application d’une impulsion de fréquence ωs + δ. L’état du spin nucléaire de 183W est ensuite lu, et la probabilité de le retrouver dans l’état final ⇓ (absence de transition) est donnée en fonction de δ ; une résonance est observée pour ωI = δ/2π = -785 kHz.
(g) Polarisation du 183W. Après préparation dans l’état ⇓, Nprep impulsions sont appliquées à la fréquence ωs -ωl. La probabilité de détecter 183W dans l’état ⇓ augmente avec Nprep, pour atteindre 0.8 après seulement quelques impulsions.
Ces résultats ouvrent la voie à l’utilisation de spins nucléaires individuels pour le calcul quantique, permettant ainsi d’accéder à des temps de cohérence supérieur à la seconde. Ils constituent aussi un premier pas vers des mesures de spectroscopie RMN sur des molécules individuelles.
Références :
[1] “Detecting spins by their fluorescence with a microwave photon counter”,
Emanuele Albertinale, Léo Balembois, Eric Billaud, Vishal Ranjan, Daniel Flanigan, Thomas Schenkel, Daniel Estève, Denis Vion, Patrice Bertet, Emmanuel Flurin, Nature 600, 434 (2021)
[2] “Single electron-spin-resonance detection by microwave photon counting”,
Z. Wang, L. Balembois, M. Rančić, E. Billaud, M. Le Dantec, A. Ferrier, P. Goldner, S. Bertaina, T. Chanelière, D. Estève, D. Vion, P. Bertet, E. Flurin, arxiv:2301.02653 (2023) – Nature 619, (2023) 276.
[3] “All-microwave readout, spectroscopy, and dynamic polarization of individual nuclear spins in a crystal”, J. Travesedo, J. O’Sullivan, L. Pallegoix, Z. W. Huang, P. Hogan, P. Goldner, T. Chaneliere, S. Bertaina, D. Esteve, P. Abgrall, D. Vion, E. Flurin, P. Bertet, arXiv:2408.14282, Science Advances 11(10) (2025) eadu0581.
[4] « Enhancing the sensitivity of single microwave photon detection with bandwidth tunability”, L. Pallegoix, J. Travesedo, A. S. May, L. Balembois, D. Vion, P. Bertet, E. Flurin, arXiv:2501.0735
[5] “Controlling spin relaxation with a cavity”,
A. Bienfait, J. J. Pla, Y. Kubo, X. Zhou, M. Stern, C. C. Lo, C. D. Weis, T. Schenkel, D. Vion, D. Esteve, J. J. L. Morton, P. Bertet, Nature 531, 74 (2016)
[5] « Une nouvelle méthode de polarisation des noyaux atomiques dans les solides », A. Abragam, W. Proctor,. C.R. Acad. Sci. Paris, 2253 (1958)
Voir aussi :
Individual solid-state nuclear spin qubits with coherence exceeding seconds.
O’Sullivan, J., Travesedo, J., Pallegoix, L. Zhiyuan W. Huang, Patrick Hogan, Alexandre S. May, Boris Yavkin, Sen Lin, Ren-Bao Liu, Thierry Chaneliere, Sylvain Bertaina, Philippe Goldner, Daniel Estève, Denis Vion, Patrick Abgrall, Patrice Bertet & Emmanuel Flurin, Nat. Phys. 21, 1794–1800 (2025).
Faits marquants antérieurs :
- Détection de la résonance de spin d’un électron unique, par comptage de photons micro-ondes (2023),
- RPE : Détection de de la réponse de spins individuels avec un capteur de photon unique (Décembre 2021)
- Contrôler la relaxation de spin avec une cavité (Février 2016)
Contact CEA : Patrice Bertet (SPEC/Quantronique)