Les circuits électroniques exploitant les lois de la mécanique quantique ont émergé, ces dernières années, comme une plate-forme permettant de réaliser des tâches hors de portée des circuits classiques. On peut penser, par exemple, aux promesses du calcul quantique ou de l'électronique moléculaire, mais les circuits quantiques permettent également de réaliser des amplificateurs de sensibilité ultime, de communiquer via des champs électromagnétiques non-classiques, etc…
La réalisation d'un circuit quantique n'est cependant pas aussi simple que celui d'un circuit classique où il suffit de rassembler et connecter des composants. Dans le monde quantique, chaque composant intéragit avec l'ensemble des éléments du circuit, ce qui conduit à de nouelles règles d'assemblage. Dans un article paru dans la revue en ligne en accès libre Physical Review X [1], des chercheurs des groupes Nanoélectronique et Quantronique du SPEC établissent ces nouvelles règles pour une large classe de composants quantiques, ouvrant ainsi la voie à une ingénierie des circuits quantiques.
Les circuits électroniques exploitant les lois de la mécanique quantique ont émergé, ces dernières années, comme une plate-forme permettant de réaliser des tâches hors de portée des circuits classiques. On peut penser, par exemple, aux promesses du calcul quantique ou de l'électronique moléculaire, mais les circuits quantiques permettent également de réaliser des amplificateurs de sensibilité ultime, de communiquer via des champs électromagnétiques non-classiques, etc…
Comme pour les circuits classiques, le développement de circuits quantiques avec des fonctionnalités riches nécessitera de combiner plusieurs composants quantiques. Cependant, l'ingénierie nécessaire pour concevoir de tels circuits est encore incomplète, notamment pour les circuits maintenus hors d'équilibre par des sources de tension. En effet, dans un circuit quantique les composants sont interdépendants : vu de chaque composant, le reste du circuit peut être considéré comme « l'appareil de mesure » du-dit composant, modifiant son comportement de façon non-linéaire. Par conséquent, à la différence des composants classiques, lorsqu'on met deux composants quantiques en série, on ne peut pas ajouter leurs résistances qui auraient été mesurées indépendamment au préalable et il faut donc trouver de nouvelles « règles de composition ». C'est objet des recherches conduites par les équipes Nanoélectronique et Quantronique du SPEC.
Jusqu'ici ces nouvelles règles de composition n'étaient connues que pour un seul composant : la jonction tunnel. L'interaction de ce composant avec le circuit environnant est en effet bien décrite par la théorie du « blocage de Coulomb dynamique » développée au début des années 90 notamment par le groupe Quantronique.
Dans les années 80, Rolf Landauer et Markus Büttiker (entre autres) ont montré qu'on peut décrire le transport électrique dans un composant quantique comme une diffusion cohérente d'électrons, chaque « patte » du composant étant vue comme un guide d'ondes électroniques. Cette approche est très générale car elle s'affranchit de tout modèle spécifique de composant. Elle fournit néanmoins des prédictions très concrètes, telle la fameuse « formule de Landauer » qui relie la conductance électrique G aux probabilités {Tn} de transmission des différents modes électroniques : G=(e²/h)ΣTn . Cette dernière formule explique notamment le spectaculaire phénomène de « conductance quantifiée » à des multiples de (e²/h) lorsque les Tn valent soit 0 soit 1, tel que dans les constrictions réalisées dans des conducteurs balistiques ou dans l'effet Hall quantique. Or, assez paradoxalement, l'approche de Landauer et Büttiker ne peut pas être utilisée dans des circuits quantiques : bien que les composants considérés soient quantiques, ils sont supposés connectés à des réservoirs d'électrons classiques dont le potentiel est parfaitement bien défini. Au contraire, dans un circuit quantique chaque nœud du circuit voit son potentiel électrique fluctuer quantiquement (voir Fig. 1).
Les chercheurs du SPEC ont d'abord montré qu'il était possible –sous certaines conditions– d'incorporer ces fluctuations quantiques du potentiel dans la description de Landauer et Büttiker, et donc de comprendre comment ces fluctuations affectent le transport des électrons de façon générique. Cette approche revient à réaliser une synthèse entre la description de Landauer et Büttiker et la théorie du blocage de Coulomb dynamique qui n'est dès lors plus restreinte aux jonctions tunnel. Cette synthèse apporte quelques surprises : non seulement la « formule de Landauer » n'est généralement pas valable dans les circuits quantiques, mais les fluctuations peuvent, en outre, modifier les probabilités de transmission des différents modes par un effet électrostatique révélé par ce travail.
Dans un deuxième temps, en supposant que les fluctuations sont approximativement gaussiennes, les chercheurs ont explicité le jeu d'équations permettant de déterminer complètement lesdites fluctuations (et simultanément la conductance, via les relations fluctuation-dissipation). Cette approche permet donc de prédire le comportement d'un composant « mesuré » par un circuit quelconque, généralisant ainsi les règles de combinaison des jonctions tunnel à des composants quantiques plus généraux.
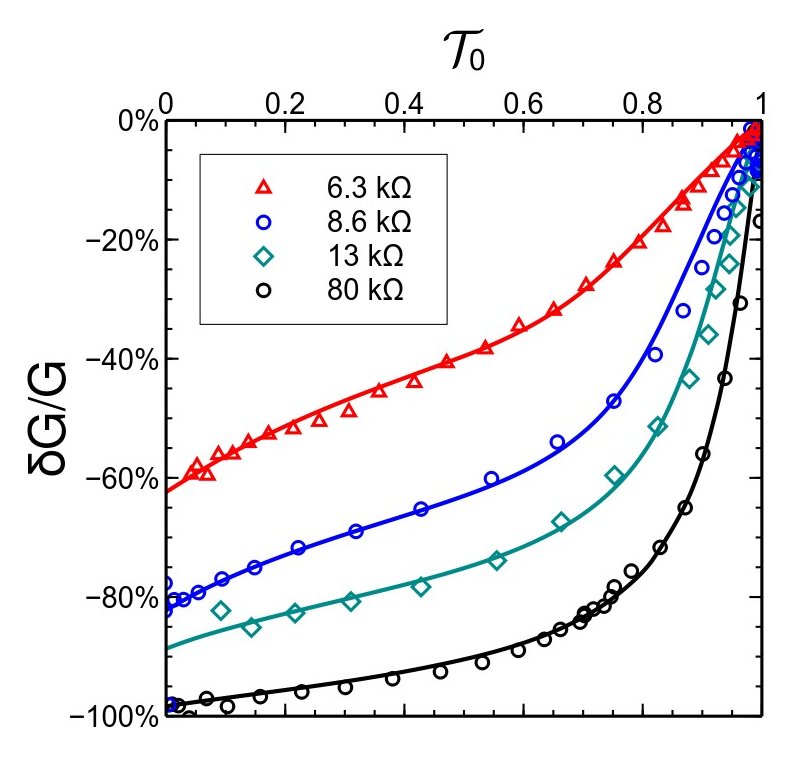
Pour illustrer les progrès permis par leur approche, les chercheurs du SPEC ont finalement montré qu'ils pouvaient expliquer précisément une série d'expériences pour lesquelles jusqu'ici il n'existait pas de théorie satisfaisante (voir Fig. 2). Dans ces expériences, Frédéric Pierre et son équipe (CNRS Marcoussis), avaient mesuré comment la conductance d'un « contact ponctuel quantique » réalisé dans un gaz d'électron bidimensionnel était modifiée quand on lui ajoute une résistance en série [2].
Ce travail devrait ouvrir de nouvelles perspectives pour l'ingéniérie des circuits quantiques. En effet il va permettre de transposer aux circuits quantiques les très nombreux résultats obtenus dans l'approche de Landauer et Büttiker tels, par exemple, ceux portant sur le transport de chaleur. Ce travail fournit également une théorie plus générale du couplage des circuits quantiques hors d'équilibre au champ électromagnétique que celle disponible actuellement.
Références :
[1] Interacting electrodynamics of short coherent conductors in quantum circuits
C. Altimiras, F. Portier et P. Joyez,, Phys. Rev. X 6, 000000 (2016).
[2] Experimental test of the dynamical coulomb blockade theory for short coherent conductors
C. Altimiras, U. Gennser, A. Cavanna, D. Mailly, and F. Pierre, Phy. Rev. Lett. 99, 256805 (2007),
Strong back-action of a linear circuit on a single electronic quantum channel,
F. D. Parmentier, A. Anthore, S. Jezouin, H. le Sueur, U. Gennser, A. Cavanna, D. Mailly and F. Pierre
Nat. Phys. 7, 935‑938 (2011),
Tomonaga–Luttinger physics in electronic quantum circuits,
S. Jezouin, M. Albert, F.D. Parmentier, A. Anthore, U. Gennser, A. Cavanna, I. Safi and F. Pierre,
Nat. Commun. 4, 1802 (2013).