La spectroscopie théorique a pour objectif de calculer la réponse de la matière à une excitation, qui peut être un rayonnement électromagnétique ou un faisceau d’électrons. La comparaison avec l’expérience permet d’aider à l’interprétation des mesures, d’identifier les phénomènes prédominants, ou de valider le niveau d’approximation du formalisme.
L’état de l’art de la spectroscopie théorique repose sur les calculs ab initio, c’est-à-dire à partir des premiers principes. Parmi ceux-ci, la théorie de la fonctionnelle de la densité dépendant du temps (TD-DFT) est un formalisme précis et relativement léger permettant d’obtenir les spectres de perte d’énergie d’électrons et d’absorption. Dans le cas des cristaux infinis (3D), la périodicité permet de travailler en espace réciproque, ce qui rend les codes de calculs extrêmement efficaces.
L’intérêt pour les propriétés exceptionnelles des nano-matériaux a conduit à tenter d’utiliser ce cadre périodique pour étudier les nano-objets isolés, en les introduisant dans une supercellule. L’équipe de Spectroscopie Théorique montre que le formalisme développé pour les cristaux 3D ne peut être appliqué sans être fondamentalement adapté pour les objets bidimensionnels isolés (2D). Cette analyse théorique clarifie la nature de la réponse optique (coefficient de réflexion, transmission ou d’absorption sur l’ensemble du spectre) obtenue en TD-DFT pour une couche ultra-mince et établit un formalisme pour la calculer correctement.
La théorie de la fonctionnelle de la densité (DFT) est parfaitement adaptée pour décrire l’état fondamental d’un milieu et toutes ses propriétés. Pour atteindre les propriétés optiques et la réponse à une excitation optique, la méthode est étendue par l’introduction d’un potentiel oscillant dépendant du temps. Cette méthode TD-DFT (pour l’anglais Time-Dependent-DFT) repose sur un formalisme bien établi depuis les années 1960 [1]. Pour un cristal infini, la prise en compte de la périodicité conduit à réaliser le calcul dans l’espace réciproque et la formule d’Adler et Wiser [2, 3] permet d’en déduire la fonction diélectrique macroscopique et le spectre d’absorption.
Pour les nanomatériaux, qui présentent des propriétés nouvelles, leur taille finie doit être prise en compte. Ceci conduit à utiliser ce formalisme périodique en remplaçant la cellule cristalline unitaire par une supercellule, qui contient les plans atomiques entourés de vide de part et d’autre, l’ensemble étant répété périodiquement. Il apparaît cependant que la présence du vide ainsi pris en compte et celle des répliques conduisent à une fonction de réponse non physique pour l’objet 2D isolé.
Afin de résoudre cette difficulté, un nouveau formalisme a été développé par l’équipe de Spectroscopie Théorique du LSI [4]. La méthode décrit la couche isolée à l’aide de fonctions de réponse auxiliaires périodiques de période égale à l’épaisseur de matière. En résolvant l’équation de la TD-DFT dans un sous-espace de vecteurs du réseau réciproque (nx2π/L, méthode « Selected-G »), on obtient des spectres indépendants de la taille de la supercellule, tout en gardant l’efficacité des codes en espace réciproque. La méthode a été appliquée avec succès pour le calcul du spectre d’absorption de surfaces, ainsi qu’au calcul de spectres de perte d’énergie d’électrons de couches mince de graphène [5,7].
La question du spectre d’absorption de la couche mince restait sujet à débat. Le travail s’est donc poursuivi et a permis de mettre en évidence les raisons pour lesquels le formalisme 3D ne s’applique plus aux objets 2D, de clarifier la nature de l’observable calculée en TD-DFT, ainsi que la méthodologie qui permet de l’obtenir.
Cette autre partie du travail a consisté à décrire la couche mince dans le cadre du modèle de Lorentz (voir Figure), où les électrons sont décrits de façon classique comme étant reliés à leur noyau par une force élastique, et à étudier leur réponse à un champ électrique oscillant. Il a alors pu être établi que pour un objet quasi-2D, le champ électrique induit parallèlement au plan de la couche est négligeable, et montré que la composante longitudinale de l’excitation donne naissance à une polarisation transverse.
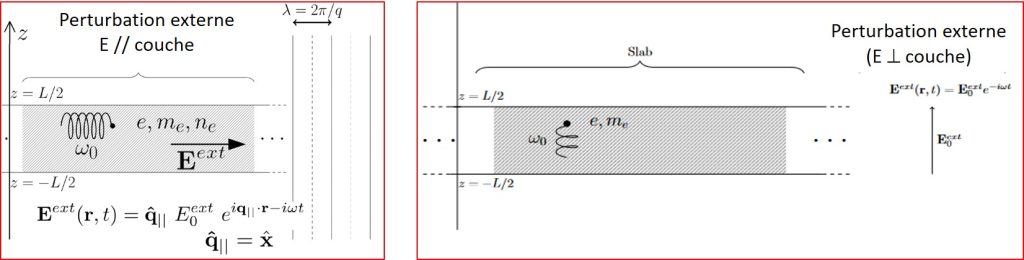
Fig. 1 : Schéma d’une couche mince d’épaisseur L, soumise à une excitation électromagnétique de vecteur d’onde q et de fréquence ω, dont le champ électrique possède des composantes parallèle et perpendiculaire à la couche. Selon le modèle de Lorentz, les électrons de charge e-, de masse me et de densité ne sont considérés comme des oscillateurs harmoniques classiques de fréquence caractéristique ω0.
- À gauche : pour la composante du champ parallèle à la surface de la couche, de vecteur d’onde q// : contrairement à un volume infini, la présence des 2 interfaces de la couche mince, induit un champ électrique dans la direction orthogonale à la surface. Pour L<< λ, le champ électrique induit est beaucoup moins intense que celui qui serait induit en volume. Le système n’est alors plus capable de maintenir une excitation collective à la fréquence du plasma, et la fonction de réponse de la couche tend vers le spectre d’absorption.
- À droite : pour la composante du champ perpendiculaire à la surface de la couche (L<< λ), le champ électrique induit a la même intensité qu’en volume et la couche est alors capable d’entretenir une oscillation collective des électrons dans cette direction (excitation plasmon).
La réponse d’une couche mince à une excitation quelconque présente ainsi la double signature d’un pic d’absorption et d’excitations collectives plasmons, en accord avec les calculs de TD-DFT.
En revenant à la définition du tenseur diélectrique macroscopique, ces résultats montrent pourquoi la fonction diélectrique macroscopique ne peut plus être calculée à partir de la formule d’Adler et Wiser [2, 3], et ont permis d’établir une nouvelle expression de cette grandeur [5, 6].
Le formalisme de la TD-DFT en espace réciproque, avec la méthode « Selected-G » pour un objet quasi-2D isolé [4], a été utilisé pour étudier une couche de ~2 nm d’épaisseur de silicium, dont la résonance d’absorption est située à ~4 eV et la fréquence plasma à ~17 eV. On observe alors que la fonction de réponse change brutalement lorsqu’on augmente l’épaisseur de la matière d’environ 0.5 nm par rapport à l’extension des positions atomiques (Voir Fig. 2 – comparaison des spectres marron et orange) : il apparaît un pic à ~17 eV, c’est-à-dire à la fréquence plasmon. L’épaisseur ajoutée correspond à la distance nécessaire pour que la fonction de réponse (décrite en espace réel) s’annule, et se révèle définir l’interface entre l’objet quasi-2D et le vide. Ainsi la réponse optique d’un objet-quasi 2D calculée en TD-DFT, pour une excitation selon une direction qx +/- qz est une combinaison linéaire de l’absorption et du plasmon (spectres rouge et vert à droite), contrairement à la fonction de réponse de l’objet massif qui donnerait des spectres similaires à ceux de la figure 2-gauche, avec un pic unique à ~4 eV, quelle que soit la direction d’excitation. Cette composante à 17 eV montre également que la réponse calculée en TD-DFT ne permet pas d’accéder à la réponse transverse pour une excitation perpendiculaire à la couche mince.
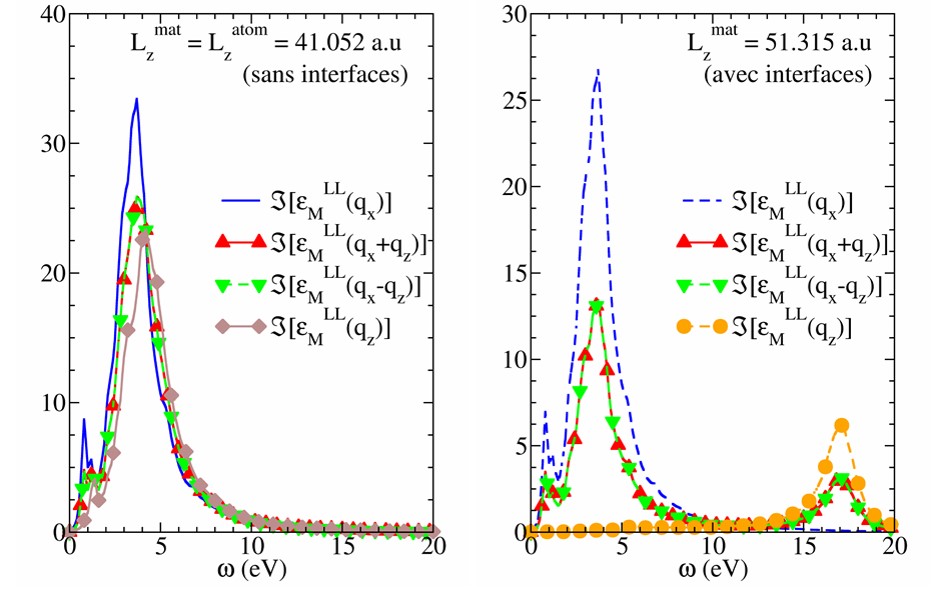
Fig. 2 : A gauche : coefficient d’absorption (partie imaginaire de la composante zz du tenseur diélectrique) d’une couche mince de 2 nm de silicium, présentant une résonance d’absorption à ~4 eV. À droite : même grandeur calculée en ajoutant une épaisseur d’interface de 0.5 nm, ce qui fait apparaitre une absorption supplémentaire vers ~17 eV, à la fréquence plasmon. Ce pic supplémentaire n’est pas présent si l’on considère la surface d’un objet 3D, et est directement lié à la nature du système 2D.
Pour exploiter ce résultat, la réflectance, la transmittance et l’absorbance ont été calculées à partir du modèle d’électromagnétisme classique d’Airy, en considérant une lumière polarisée p (Fig. 3). Les spectres correspondants sont présentés sur la figure 4 (noir, rouge et vert) : on observe qu’ils présentent tous une double structure à ~ 4eV et à ~17eV. Le développement limité à l’ordre 1 en fonction de l’épaisseur de matière des formules d’Airy confirme que ces deux résonances correspondent bien à l’absorption et au plasmon. Ces spectres, fondamentalement différents de la réflectance sur une surface (formule de Fresnel – courbe bleue tiretée), résultent de la présence de la seconde interface avec le vide [5, 7].
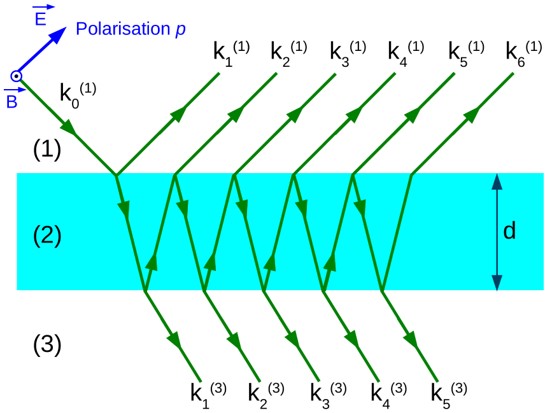
Figure 3 : Modèle d’Airy : série de réflexions et transmissions d’un champ électromagnétique de polarisation p sur aux interfaces d’une couche mince.
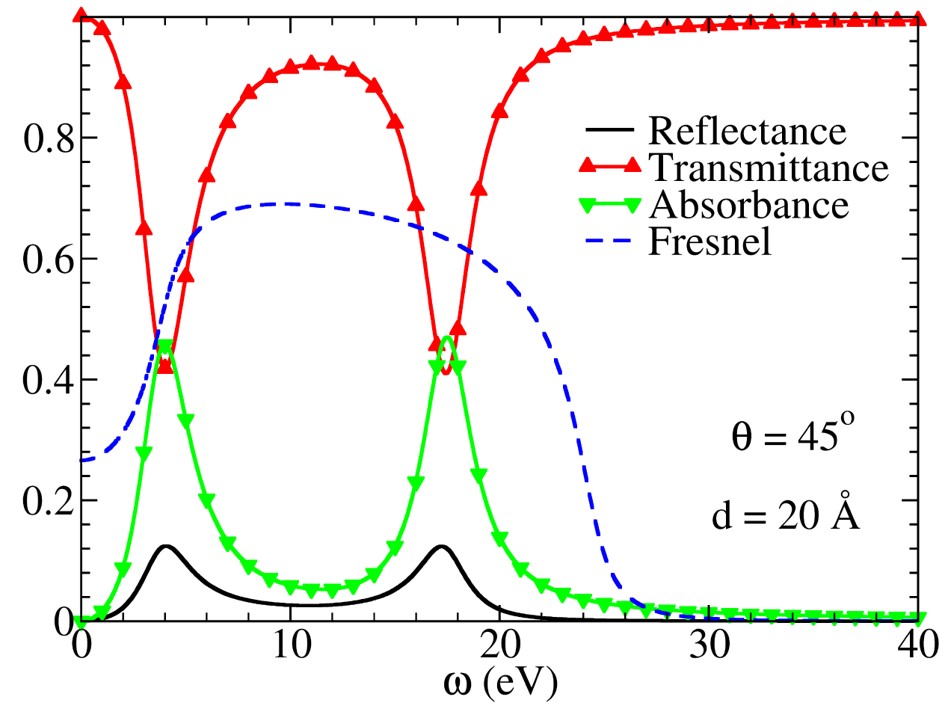
Figure 4 : Variation du facteur de transmission (courbe rouge ▲), réflexion (courbe noire) et d’absorption (▼) d’un champ électromagnétique incident de polarisation p, éclairant une couche ultra-mince de silicium. Par comparaison, la courbe bleue-tiretée donne le coefficient de réflexion selon la formule simple de Fresnel (dont l’application suppose que l’on considère un solide 3D). Ce résultat est essentiellement différent du résultat du modèle donné par la courbe noire, résultat du calcul TD-DFT pour un plan atomique 2D.
Ce travail a ainsi montré l’importance de réinterroger les formalismes théoriques et a permis :
- d’identifier les raisons pour lesquelles le formalisme 3D ne s’applique plus aux objets 2D,
- d’établir une nouvelle formule pour calculer le spectre d’absorption dans le plan de la couche,
- de donner un critère pour définir l’extension de la matière à considérer,
- de montrer que la TD-DFT ne permet pas d’accéder à la réponse transverse pour une perturbation perpendiculaire à la couche
- et de préciser la nature de l’observable calculée en TD-DFT.
Ainsi, le formalisme de la TD-DFT permet toujours de calculer la réponse optique d’une couche ultra-mince, mais l’observable obtenue n’est plus la constante diélectrique macroscopique usuelle (permittivité) conduisant au spectre d’absorption, comme c’est le cas pour un matériau massif, mais la transmittance ou la réflectance, qui sont fonction des spectres d’absorption et de plasmon.
En perspective de ce travail il reste à inclure les effets excitoniques et étudier le cas d’autres types de nano-objets (nanotubes, clusters).
Références :
[1] « The Optical Properties of Solids », edited by J. Taux (1966) p. 106, H. Ehrenreich
[2] « Quantum Theory of the Dielectric Constant in Real Solids »,
S. L. Adler, Phys. Rev. 126 (1962) 413.
[3] « Dielectric Constant with Local Field Effects Included »,
N. Wiser, Phys. Rev. 129 (1963) 62
[4] « Optical properties of surfaces with supercell ab initio calculations: Local-field effects », N. Tancogne-Dejean, C. Giorgetti and Valérie Véniard, Phys. Rev. B 92 (2015) 245308
[5] « Second Harmonic Generation from silicon surfaces functionalized with DNA nucleobases: an ab initio description« , Stefano Mazzei, PhD Thesis, IPP, December 2021.
[6] « Optical response of two-dimensional systems: Insights from classical electromagnetism to calculations » , S. Mazzei and C. Giorgetti, Phys. Rev. B 106 (2022) 035431
[7] « Optical properties of quasi-two-dimensional objects from time-dependent density functional theory: Longitudinal versus transverse dielectric functions » , S. Mazzei and C. Giorgetti, Phys. Rev. B 107 (2023) 165412.
Contact CEA-IRAMIS : Christine Giorgetti, Groupe de Spectroscopie théorique, Laboratoire des Solides Irradiés – LSI – UMR7642 (CEA, CNRS, IPP).