Mise en évidence d’une relaxation thermo-mécanique dans un liquide usuel après cisaillement

Il est communément admis que les ondes de cisaillement ne se propagent pas dans un milieu liquide. L’énergie des ondes de cisaillement est supposée se dissiper presque instantanément. Pourtant, de récents travaux expérimentaux et théoriques montrent que les liquides peuvent propager les ondes de cisaillement, comme le font les solides, mais à l’échelle confinée. Nous nous proposons d’explorer une des propriétés « de l’état solide » les plus remarquables : la thermo-élasticité. L’effet thermo-élastique découvert par Joule et décrit par Kelvin, reflète la capacité d’un solide à convertir une déformation en variation de température et vice-versa. En confinant un liquide (glycérol) entre deux surfaces mouillantes séparées à l’échelle sub-millimétrique et en le soumettant à une soudaine déformation en cisaillement (fonction échelon), nous mettons en évidence une réponse thermique quasi-instantanée du liquide; une zone chaude et une zone froide apparaissent, symétriques en amplitude, et relaxant de manière complémentaire, en l’absence d’apport d’énergie.

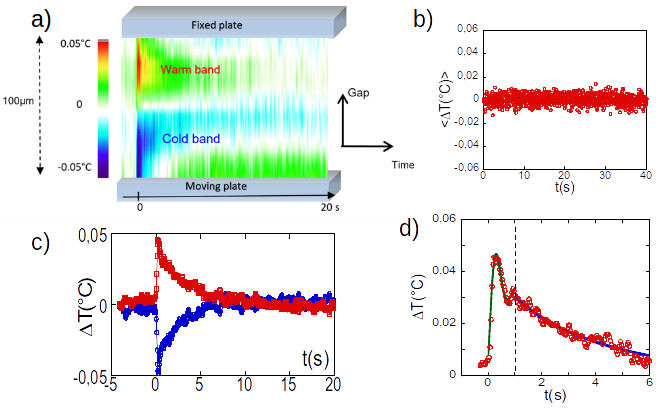
Mise en évidence d’une relaxation thermique après déformation mécanique en cisaillement dans un liquide (couche de glycérol d’épaisseur: 100 μm, mesures à température ambiante). a) Cinétique thermique de la relaxation liquide. b) Valeur moyenne de la température au cours de la relaxation. c) Détails de la réponse thermique (zones chaudes et froides). d) Modélisation de la relaxation thermique (les lignes vertes et bleues représentent l’ajustement des équations).

Cette relaxation thermique se compose d’une réponse échelonnée de type second ordre, suivie d’une deuxième phase (longue) de relaxation, qui est décrite par une décroissance exponentielle étirée ΔΤ=ΔΤmax(e^-t/τ)^β définissant un temps de relaxation thermique de plusieurs secondes (figure). Les changements thermiques et la longue relaxation thermique mettent en évidence la capacité du liquide à convertir l’énergie de déformation en états thermodynamiques se compensant de manière adiabatique. Les effets thermiques dépendent presque linéairement de l’amplitude de la déformation, accréditant l’hypothèse d’une propagation d’onde de cisaillement (corrélations élastiques) s’étendant jusqu’à plusieurs centaines de microns. Ce nouvel effet physique dévoile un comportement collectif en accord avec l’existence de corrélations à longue distance, c’est-à-dire en termes de propriétés phononiques sous-jacentes.

Contacts : Eni Kume et Laurence Noirez (LLB/NFMQ).

Le bal des pinçons

Bérengère Dubrulle (SPEC/SPHYNX)

Tous les fluides qui nous entourent (océan, atmosphère, rivières, …) obéissent aux équations de Navier-Stokes, des équations non-linéaires dont on ne sait toujours pas si elles sont bien posées mathématiquement ou non : ont-elles une solution unique ? Développent-elles des singularités ? Sous quelle forme ? En attendant de pouvoir observer des possibles indices de ces singularités dans notre nouvelle expérience GVK (Giant Von Karman), nous avons imaginé à quoi pourraient ressembler ces singularités, en nous basant sur des propriétés des équations de Navier-Stokes. Ce seraient de petites structures localisées, munies d’une direction privilégiée (un « spin ») autour de laquelle les lignes de courant se resserrent, formant un pincement (voir Fig.(a)). Nous avons donc décidé de nommer ces entités des « pinçons », représentant les structures fondamentales (les « particules ») de la turbulence à la plus petite échelle. Comme les autres particules de la physique, ces entités peuvent interagir entre elles, ou être influencées par un champ de vitesse extérieur.

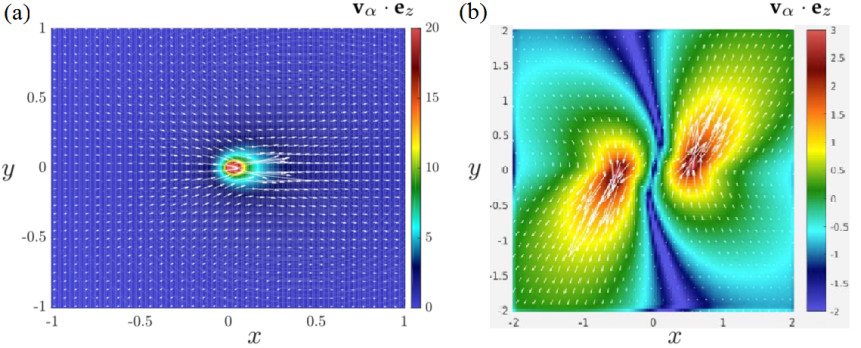
a) Champ de vitesse produit par un pinçon isolé. b) Deux pinçons en interaction. Les flèches représentent la vitesse dans le plan d’observation, alors que la couleur code la vitesse perpendiculaire au plan.

Cette dynamique est Hamiltonienne. Les interactions sont à longue portée et anisotropes. Nous sommes loin du modèle d’Ising ! Pourtant, leur mouvement est régi par certaines propriétés simples et intuitives : un pinçon voyage à la vitesse du champ généré par les autres pinçons ou par un champ extérieur. Son « spin » est orienté et déformé par le cisaillement généré par les autres pinçons ou un champ extérieur. Finalement, les pinçons se repoussent entre eux (voir Fig.(b) ). Est-ce qu’ils peuvent subir des transitions de phase ? Comment interagissent-ils en présence de bords ? Décrivent-ils la dynamique de la turbulence à petite échelle ? Autant de questions non résolues, que nous essaierons de résoudre dans les années à venir.

Contact : Bérengère Dubrulle (SPEC/SPHYNX)