Les transitions de phase sont des phénomènes physiques bien connus, qui font partie de notre vie quotidienne : l’eau liquide gèle à 0°c, bout à 100 °C ; certains métaux comme l’étain (étain blanc et étain gris) changent de structure cristalline en fonction de la température… Mais certaines de ces transitions peuvent être de nature bien différente, en lien avec l'existence de défauts « topologiques », qui ne peuvent apparaitre ou disparaitre qu'accompagnés de leurs anti-défauts
Une collaboration de théoriciens et d'expérimentateurs, dont des spécialistes de diffusion de neutrons, s’est intéressée à un matériau quantique unidimensionnel : BaCo2V2O8 (BACOVO). L'étude montre qu’il s’agit d’un système modèle pour l’étude d’une nouvelle transition de phase topologique, gouvernée non pas par un seul, mais par deux types d’excitations topologiques, qui sont de plus quantiquement conjuguées : l'application d'un champ magnétique externe permet de piloter, le système que l'on peut placer dans chacune des phases où une des deux excitations est dominante.
Le concept de transition de phase est un concept fructueux en physique, utile en cosmologie, en physique des particules, comme en matière condensée. Une transition de phase se manifeste par un changement soudain d'état de la matière, et est généralement caractérisée par un changement (« brisure ») de symétrie. Cependant, depuis les idées de Berezinskii, Kosterlitz et Thouless (Prix Nobel de Physique 2016), une nouvelle classe de transitions de phase a été découverte [1]. Ces transitions de phase dites « topologiques » ne présentent pas de rupture de symétrie, mais sont caractérisées par la présence de « défauts topologiques », tels que des objets de type soliton (ou vortex), singularités qui ne peuvent être éliminées que si elles sont annihilées par leurs anti-défauts. À haute température, les défauts (et anti-défauts) prolifèrent. A basse température, au contraire, les défauts et anti-défauts tendent à s’apparier, de sorte qu’en moyenne le système apparait uniforme : tout se passe comme si les défauts n’étaient plus présents. La transition entre les 2 états définit la transition de phase « topologique ».
Si cette situation est maintenant bien comprise, de nombreuses théories ont été élaborées pour tenter d’appréhender le cas où le diagramme de phase est gouverné par deux familles d’excitations topologiques en compétition. Mais est-ce possible en pratique ? Peut-on obtenir une réalisation expérimentale de cette situation, et si oui, que se passe-il ? Notre équipe, a pu apporter la première réponse expérimentale et théorique à ces questions.
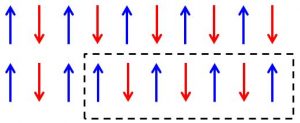
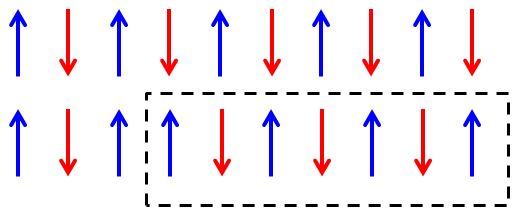
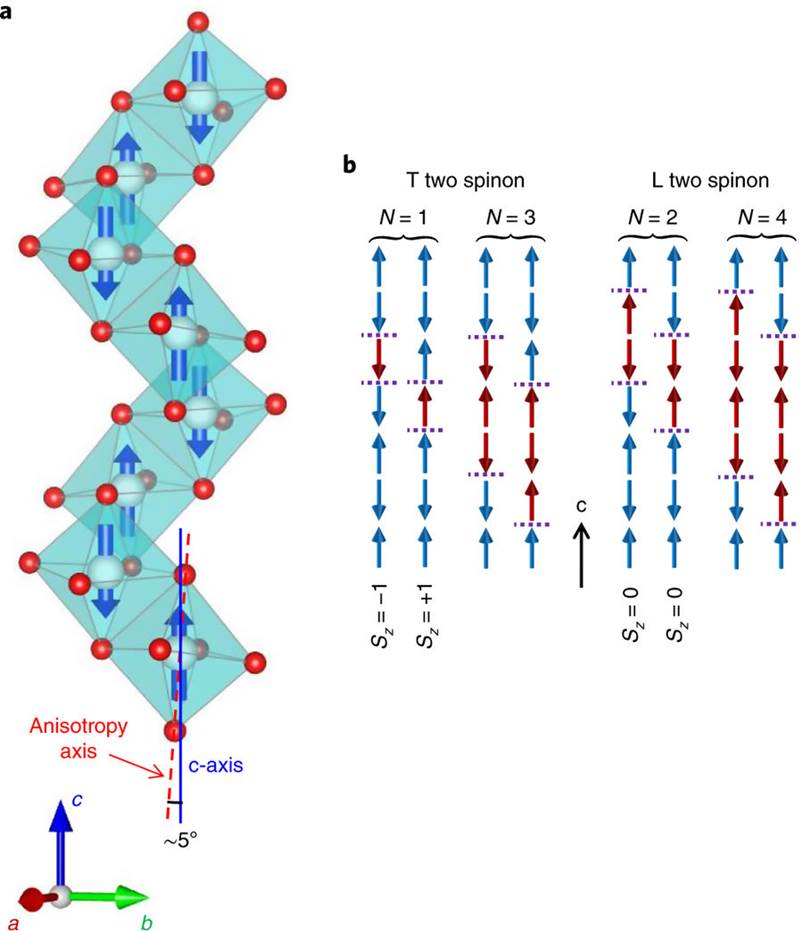
Le matériau étudié est un oxyde magnétique de cobalt, BaCo2V2O8 (BACOVO), que l’on peut voir comme une réalisation d'une chaine de spin unidimensionnelle (modèle d'Ising1D) : les moments magnétiques sont fortement contraints de s'aligner dans la direction de chaines « z », par le biais d’une interaction d'échange antiferromagnétique. Pour ce système les excitations topologiques s’apparentent à des parois, mobiles le long de l'axe z, séparant deux domaines parfaitement ordonnés où l'orientation des spins Sz suit la séquence parfaite : « up-down-up-down »… Dans ce contexte, la diffusion de neutrons, sensible à l'ordre magnétique, est l'outil incontournable pour « voir » et caractériser entièrement les configurations magnétiques, ainsi que leur spectre d'excitations.
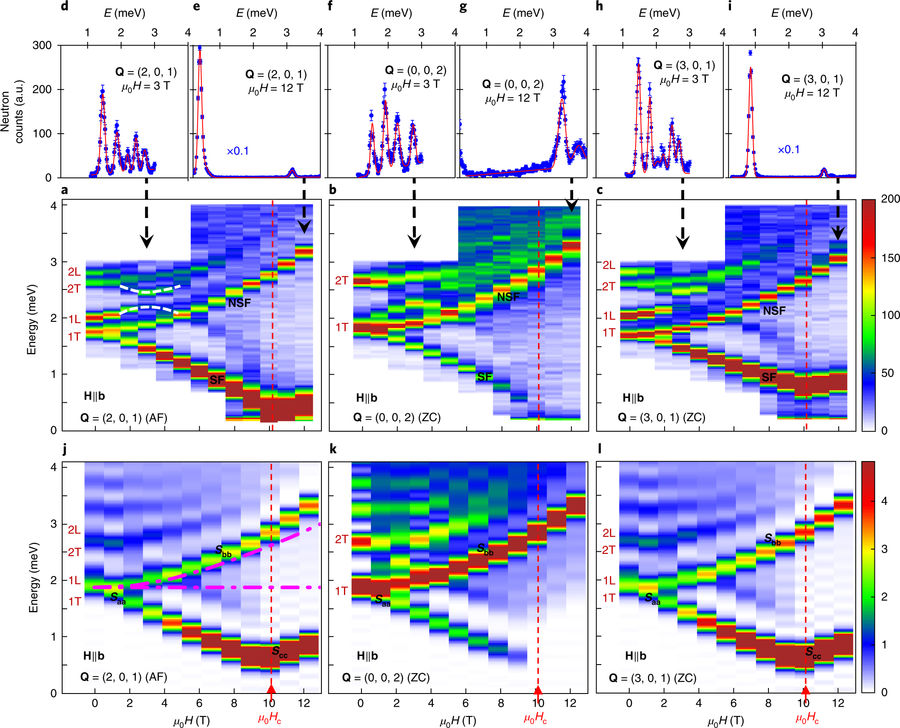
La structure cristallographique de BACOVO est en outre très particulière : lorsqu’on applique un champ magnétique uniforme externe perpendiculaire à l’axe « z », par exemple selon l’axe « x », cette structure conduit à l’apparition de champs magnétiques locaux alternés dans la troisième direction « y ». Cet effet polarise subtilement les moments magnétiques qui tendent à s'aligner également selon une structure alternée pour la composante de spin Sy. Il en résulte un deuxième jeu de défauts topologiques, qui correspondent là aussi à des parois de domaine, mais pour la composante de spin Sy. Le point clef est que l’on est alors en présence de deux modes d’excitations quantiquement conjugués l’une de l’autre Sy et Sz, qui ne peuvent être déterminées simultanément. Le diagramme de phase est alors gouverné par la « compétition » entre les deux excitations. En fonction de l'intensité du champ magnétique appliqué, on observe expérimentalement une valeur critique du champ, de l’ordre de 10 T, qui sépare deux phases « basse température », l’une essentiellement gouvernée par les excitations « z » et l’autre par les excitations « y ». Là encore, les expériences de diffusion de neutrons, permettent de caractériser entièrement l’évolution des configurations magnétiques et déterminer le spectre des excitations en fonction du champ magnétique appliqué.
Ces mesures ont été parfaitement reproduites et interprétées par les calculs de théorie des champs menés par les théoriciens de l’Université de Genève. L'équipe met ainsi en évidence la possibilité d'une nouvelle classe de transition de phase topologique, gouvernée non pas par un seul, mais par deux types d’excitations topologiques quantiquement conjuguées. L'étude en fonction du champ magnétique appliqué révèle les mécanismes fins de cette transition, et décrit comment un type de défauts peut dominer l’autre et contrôler ainsi la transition [3]. Cette étude fondamentale de physique de la matière condensée, par des méthodes classiques de diffusion de neutrons polarisés, fait ainsi avancer notre connaissance fondamentale de la matière, indispensable pour élaborer de nouveaux matériaux complexes possédant des propriétés spécifiques pour de multiples applications (capteurs, technologie de traitement de l'information, nouvelles énergies, …) .
[1] J.V. José, 40 years of Berezinskii-Kosterlitz-Thouless theory. World Scientific (2013).
[2] Longitudinal and transverse Zeeman ladders in the Ising-like chain antiferromagnet BaCo2V2O8
B. Grenier, S. Petit, V. Simonet, E. Canévet, L.-P. Regnault, S. Raymond, B. Canals, C. Berthier, and P. Lejay, Phys. Rev. Lett. 114, 017201 (2015) et Phys. Rev. Lett. 115, 117902 (2015).
[3] Topological quantum phase transition in the Ising-like antiferromagnetic spin chain BaCo2V2O8,
Q. Faure, S. Takayoshi, S. Petit, V. Simonet, S. Raymond, L.-P. Regnault, M. Boehm, J.S. White, M. Månsson, C. Rüegg, P. Lejay, B. Canals, T. Lorenz, S.C. Furuya, T. Giamarchi and B. Grenier, Nature Physics (2018).
Communiqué de presse de l'Université de Genève : « L’apparent calme intérieur des matériaux quantiques » / « The apparent inner calm of quantum materials« .
Contact CEA-IRAMIS : Sylvain Petit (Laboratoire Léon Brillouin).
Collaboration :
- Quentin Faure, Stéphane Raymond, Louis-Pierre Regnault & Béatrice Grenier : Univ. Grenoble Alpes, CEA, INAC-MEM, Grenoble, France
- Quentin Faure, Virginie Simonet, Pascal Lejay & Benjamin Canals : Univ. Grenoble Alpes, Institut Néel, Grenoble, France
- Shintaro Takayoshi, Christian Rüegg & Thierry Giamarchi : Department of Quantum Matter Physics, University of Geneva, Geneva, Switzerland
- Sylvain Petit : Laboratoire Léon Brillouin, CEA, CNRS, Université Paris-Saclay, CE-Saclay, Gif-sur-Yvette, France
- Martin Boehm : Institut Laue-Langevin, Grenoble, France
- Jonathan S. White, Martin Månsson & Christian Rüegg : Laboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, Villigen PSI, Switzerland
- Martin Månsson : Materials Physics, KTH Royal Institute of Technology, Stockholm, Sweden;
- Thomas Lorenz : Physikalisches Institut, Universität zu Köln, Köln, Germany ;
- Shunsuke C. Furuya : Condensed Matter Theory Laboratory, RIKEN, Wako, Saitama, Japan.