Les excitons sont des excitations élémentaires collectives de basse énergie de la matière solide, impliquant la création de paires électron-trou. Ces excitations sont au cœur de l'interaction lumière-matière et à l'origine de phénomènes aussi divers que les processus photovoltaïques ou photo-catalytiques.
Les excitons peuvent être modélisés à l'aide d'approximations simples (modèles de Frenkel ou Wannier [1] ). Cependant de nouveaux développements théoriques sont nécessaires pour rendre compte précisément des progrès récents dans les mesures expérimentales à haute résolution (spectroscopie électronique de perte d'énergie (EELS) ou la diffusion inélastique des rayons X (IXS : Inelastic X-ray Scattering).
Dans ce travail, une collaboration de chercheurs autour de l'équipe ETSF du LSI montre comment une approche ab initio à plusieurs corps peut être étendue pour traiter les excitations propagatives à grand transfert de moment [2], et aller ainsi au-delà des limitations des principes de base [1]. Les courbes de dispersion des excitons de plusieurs systèmes (LiF, Ar, BN, graphane, et solides moléculaires) [3, 4, 5, 6] ont été ainsi obtenues, suggérant de nouvelles expériences. avec la mise en évidence d'un nouveau type d'excitation élémentaire : « l'excitaron », résultant de l'interaction entre trou et exciton [7].
En modélisation, les approximations de Frenkel et Wannier [1] sont deux modèles théoriques simples d'excitons bien adaptés pour décrire les deux cas limites où les paires électrons trous (e-h) sont respectivement fortement ou faiblement liées. Pour décrire les cas des intermédiaires, l'équation de Bethe-Salpeter, permettant de décrire l'état fondamental de deux objets en interaction, est l'approche ab initio le plus générique permettant de décrire tout type d'excitons.
Expérimentalement, la spectroscopie d'absorption optique permet d'explorer la limite des grandes longueurs d'onde (q → 0), bien supérieures à la taille du système. Afin d'interpréter ce type d'expérience, il est donc utile de disposer d'un bon modèle pour décrire ce domaine d'énergie. Cependant, les excitons peuvent transporter un moment q non nul et former ainsi une structure de bande qu'il faut pouvoir modéliser. En effet, cette dispersion détermine la façon dont les paires e-h se propagent à l'intérieur du cristal et transportent l'énergie d'excitation. Cette propriété est ainsi d'une grande importance pour toutes les applications impliquant la collecte de lumière, et fournit également des connaissances fondamentales sur la mobilité et la migration des excitons.
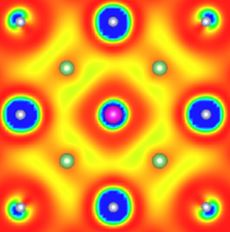
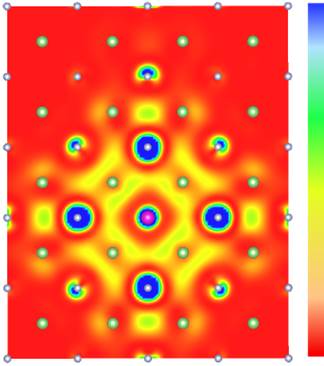
Un calcul dans le cas du cristal de LiF montre un exemple d'une telle analyse : après la création d'un trou sur l'atome de fluor (au centre de la figure), l'électron se retrouve distribué sur les atomes de fluor second voisins (voir le code couleur) plutôt que d'occuper les atomes de lithium adjacents (1er voisins, dont l'état 2s est libre d'accepter un électron). Cette image (contre-intuitive) démontre que l'exciton est bien une excitation à plusieurs corps qui ne peut pas être interprétée par une approche de particule simple.
Les récents progrès réalisés en spectroscopie électronique de perte d'énergie (EELS) ou de diffusion de rayons X inélastique (IXS), permettent de sonder les excitations électroniques, même pour les transferts de moment (q) importants. Ce sont des outils uniques pour mesurer les excitations électroniques non dipolaires et donc non optiquement détectables. Une filière particulièrement active de recherche implique la connaissance des excitations dites d-d (entre orbitales d) qui sont optiquement inactives. Leur détection permet par contre la description des excitations électronique dans les matériaux fortement corrélés (par exemple les supra-conducteurs). En outre, les nouveaux microscopes électroniques permettent aujourd'hui de réaliser des mesures de spectroscopie de pertes d'énergie avec une très haute résolution spatiale (inférieure au 1 nm). L'analyse théorique de ces expériences nécessite de déterminer la fonction diélectrique non seulement en q = 0, mais sur l'ensemble des transferts de moment accessible, afin de permettre par transformée de Fourier une description complète dans l'espace réel. Il y a donc un besoin crucial pour une contrepartie théorique aux avancées expérimentales, par une théorie ab initio permettant de décrire les excitons à grand transfert de quantité de mouvement.
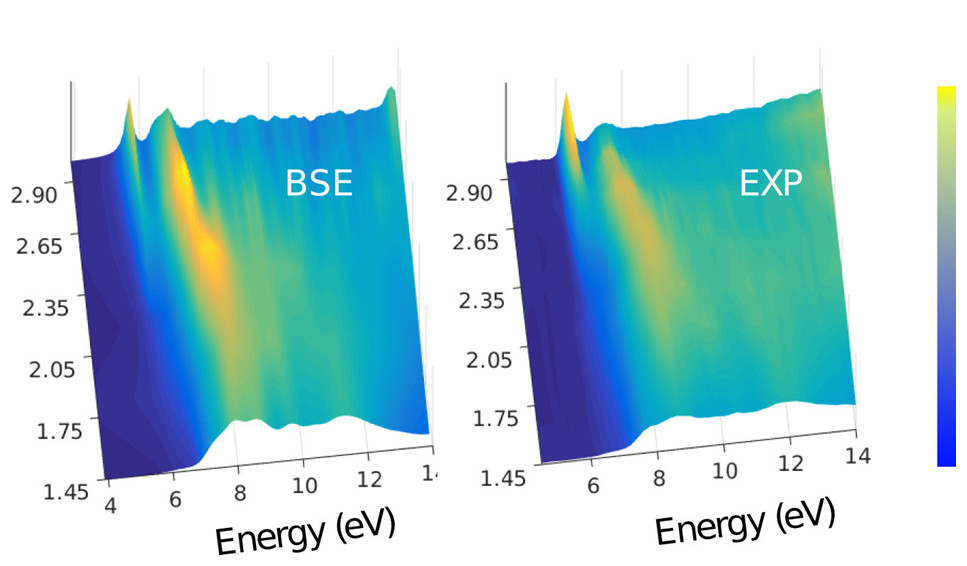
Cet écart, entre expérience et théorie, a été récemment comblé avec notre publication [1], dans laquelle il est montré comment on peut étendre l'approche ab initio à plusieurs corps, dans le cas d'un grand transfert de moment. L'ensemble de la théorie y est décrite, accompagnée d'une comparaison avec des données disponibles pour des mesures de NIXS (non-resonant inelastic X–ray scattering) à grand transfert de moment. Non seulement l'accord avec l'expérience obtenu est quantitativement bon, mais cette nouvelle approche théorique permet d'analyser pleinement l'ensemble des détails des spectres, et de complètement décrire l'exciton (via sa fonction d'onde), ainsi que la structure de bande associée.
L'approche théorique développée permet ainsi de décrire de façon fiable les excitons au sein des cristaux. Ceci doit permettre l'interprétation fine des résultats expérimentaux très détaillés, que l'on peut aujourd'hui obtenir avec les techniques les plus modernes, en particulier auprès des lignes de lumière des synchrotrons. De plus, cette approche permet maintenant d'aborder la dynamique des excitons, qui a un rôle crucial dans la description des processus photovoltaïques.
Références :
[1] Deux approches extrêmes dans leur description des excitons :
- Modèle de Frenkel : dans ce modèle, adapté aux excitations de basse énergie, les fonctions d’onde d’exciton sont constituées à partir des orbitales atomiques des atomes localisées sur les sites du réseau cristallin.
« On the transformation of light into heat in solids », J. Frenkel,Physical Review, 37 (1931) 17. - Modèle de Wannier : développement de la fonction d'onde des excitons sur des états électroniques propagatifs dans le cristal.
« The structure of electronic excitation levels in insulating crystals », G. Wannier, Physical Review 52 (3) (1937) 191.
[2] “Exciton dispersion from first principles”, M.Gatti and F.Sottile, Phys. Rev. B 88, 155113 (2013).
[3] « Frenkel versus charge-transfer exciton dispersion in molecular crystals”,
P.Cudazzo, M.Gatti, A.Rubio, F.Sottile, Phys. Rev. B 88, 195152 (2013).
[4] « Exciton dispersion in molecular solids”
P.Cudazzo, F. Sottile, A. Rubio and M.Gatti, Topical Review of J. Phys: Conden.Matter 27, 113204 (2015).
[5] « Exciton band structure in two-dimensional materials”,
P.Cudazzo, L.Sponza, C.Giorgetti, L.Reining, F.Sottile, M.Gatti, submitted to Phys. Rev. Lett.
[6] « Exciton energy-momentum map of hexagonal boron nitride”,
G.Fugallo, J.Koskelo, M.Aramini, K.Watanabe, T.Taniguchi, M.Hakala, S.Huotari, M.Gatti, F.Sottile, submitted to Phys. Rev. Lett.
[7] “Calcul des propriétés optiques et des spectres de photo-émission : un nouveau point de départ”.
Igor Reshetnyak, thèse soutenue le 21/09/2015.
Contact CEA-IRAMIS : Francesco Sottile () et Matteo Gatti () (LSI)
Collaborations :
- Simo Huotari, Department of Physics, University of Helsinki, Finland.
- Kenji Watanabe, National Institute for Materials Science, Tsukuba, Japan.
- Angel Rubio, Nano-bio Spectroscopy Group, University of San Sebastián, Spain.
- Jean-Pascal Rueff, GALAXIES beamline, Synchrotron Soleil, Gif-sur-Yvette, France.

