To change the direction of motion of a massive object, such as a car, it has to be slowed down and brought to a complete standstill first. Even the tiniest charge carriers in the universe, the electrons, follow this rule. For future ultrafast electronic components, however, it would be helpful to circumvent the electron’s inertia. Photons, the quanta of light, show how this could work. Photons do not carry mass and can thus move at the highest possible velocity, the speed of light. For a change of direction, they do not need to slow down; when they are reflected from a mirror, for instance, they abruptly change their direction without a stopover. Such behavior is highly desirable for future electronics because the direction of currents could be switched infinitely swiftly and the clock rate of processors could be massively increased. Yet, photons do not carry electric charge, which is a prerequisite for electronic devices.
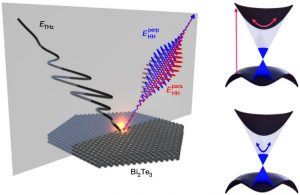
Electrons on the surface of three-dimensional topological insulators behave as massless particles, and thus move almost like light. To switch their direction of motion as rapidly as possible, the researchers accelerated them with the oscillating carrier field of light – the fastest alternating field in nature controllable by mankind – see Fig. 1.
When the electrons abruptly reverse their direction of motion, they emit an ultrashort flash of light containing a broadband spectrum of colors like in a rainbow. There are strict rules on which colours get emitted: generally, when electrons are accelerated by lightwaves, radiation is only emitted at frequencies which are integer multiples of the incident light’s frequency, so-called high-order harmonic radiation, see Fig. 2. By carefully adjusting the accelerating light field, the researchers were able to break this rule, and managed to control the electron motion so as to generate light of every imaginable colour.
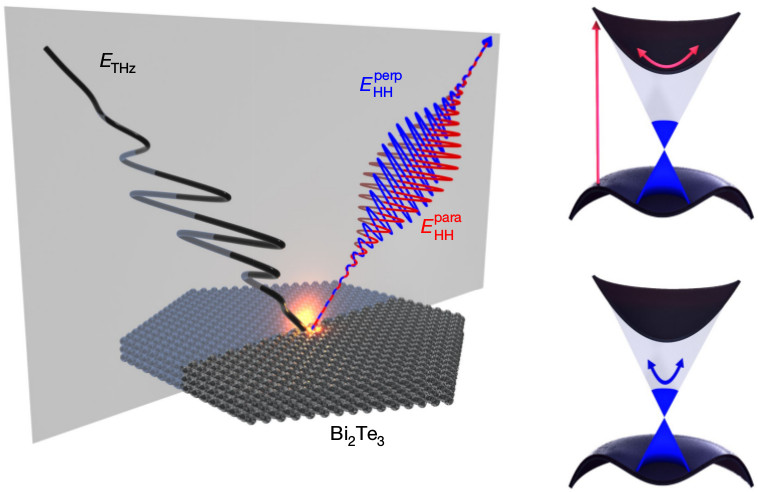
Figure 2 – HH spectral intensity for five driving frequencies between 25 THz and 42 THz. The upper curves show HH generation from the bulk. The peaks appear only at odd integer multiples of the incident frequency, and their position is independent of the pulse phase. At sub-gap frequencies, i.e. 28 THz and 25 THz for the two lower curves, only surface Dirac states contribute to HH generation, and the spectrum is qualitatively different. First, both odd and even HH peaks appear. Second (not shown), their positions — that is, the colour of the emitted light — can be continuously shifted by tuning the pulse phase. Neighbouring spectra are vertically offset for clarity.
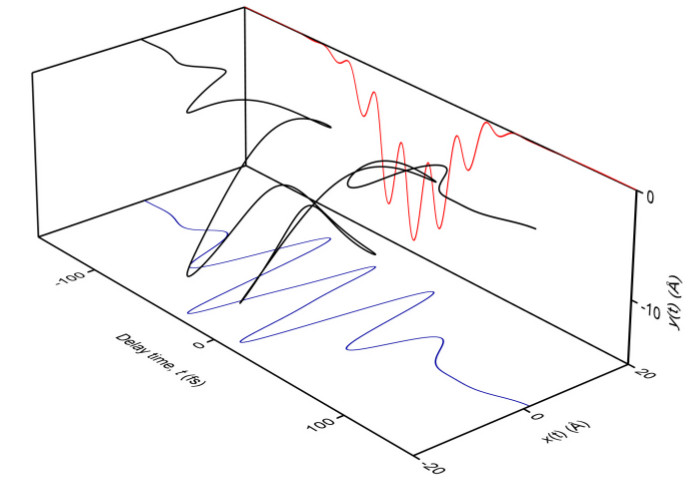
Figure 3 – Quantum simulation of ultrafast Dirac electron dynamics. The black curve shows the meandering trajectory of the center of mass of a wave packet, driven by a 25 THz field along the x direction. The trajectory results from a response parallel to the driving field (blue curve), plus an “anomalous'' one transversal to it (red curve). The latter is due to the Berry curvature of the topological surface states.
A careful analysis of the emitted radiation showed further electronic quantum properties of unusual character. In particular, electrons on the surface of a topological insulator do not move in straight lines following the driving electric field, and rather perform meandering trajectories, see Fig. 3. This “anomalous'' behaviour can be traced back to the Berry curvature of the topological band structure. Berry curvatures and the related phases are important ingredients in numerous contexts, and underpin the burgeoning field of geometric quantum transport.
Heuristically, Berry curvature imprints on electron dynamics can be modelled semiclassically. Theorists from SPEC and Regensburg were however able to validate the heuristics with fully quantum simulations. The latter also suggest that intriguing signatures of e.g. Zitterbewegung and Landau-Zener tunnelling might soon become experimentally accessible. Furthermore, such simulations provide a theoretical basis for the challenging description of geometric quantum transport in the ultrafast regime.
These results provide invaluable insights into the microscopic quantum nature of electrons, and suggest topological insulators as a promising material class for future electronics and information processing.
Reference:
Tuneable non-integer high-harmonic generation in a topological insulator,
C. P. Schmid, L. Weigl, P. Grössing, V. Junk, C. Gorini, S. Schlauderer, S. Ito, M. Meierhofer, N. Hofmann, D. Afanasiev, J. Crewse, K. A. Kokh, O. E. Tereshchenko, J. Güdde, F. Evers, J. Wilhelm, K. Richter, U. Höfer, and R. Huber, Nature 593, 385 (2021)
Contact CEA : Cosimo Gorini, Modeling and Theory Group (SPEC/GMT).
Collaboration :
- Service de Physique de l’Etat Condensé (SPEC), UMR 3680 CEA-CNRS, Université Paris-Saclay
- Institute of Experimental and Applied Physics & Institute of Theoretical Physics, University of Regensburg, Germany
- Department of Physics, Philipps-University of Marburg, Germany
- Novosibirsk State University, Sobolev Institute of Geology and Mineralogy & Rzhanov Institute of Semiconductor Physics, Siberian Branch of Russian Academy of Sciences