
Bien que le verre soit un matériau très répandu, la physique qui le gouverne fait toujours l’objet de recherches et de débats. Le verre est-il un solide ? Un liquide très visqueux qui coule extraordinairement lentement ? La question reste ouverte. En effet, lorsqu’on refroidit un liquide vitrifiable suffisamment rapidement, la cristallisation n’a pas le temps de se faire. Le matériau reste dans un état métastable appelé liquide surfondu, dont la viscosité et le temps de relaxation ta augmentent lorsque la température diminue. Par convention, la transition vitreuse est atteinte lorsque le temps de relaxation ta du liquide surfondu est égal à 100 s. Le verre a alors la consistance et les propriétés d’un solide, il est cassant. Mais à l’échelle microscopique, c’est un matériau amorphe, sans ordre à longue portée, hors équilibre, aussi désordonné qu’un liquide classique mais figé.
Il est, à présent avéré que la relaxation d’un liquide vitrifiable est un phénomène non homogène. Le matériau peut être vu, à une température donnée, comme un patchwork de petits domaines appelés hétérogénéités dynamiques (HD) [1]. A l’intérieur d’une HD, les molécules sont complètement corrélées dynamiquement, mais, en première approximation, on peut considérer que les différents domaines sont indépendants. L’ensemble des HD présente une large distribution de temps de relaxation et une distribution plus modérée de taille. Lorsque la température diminue, la taille moyenne ξ et le temps de relaxation moyen ta des domaines augmentent. La compréhension du phénomène de transition vitreuse est complètement liée à l’étude des HD.
L’idée centrale de cette étude est la suivante : faire varier la longueur des molécules pour étudier, par spectrométrie diélectrique linéaire et non linéaire à l’ordre 3, son influence sur la transition vitreuse. Assez naturellement, nous avons considéré une série d’oligomères, N-Propylène Glycol, OH-[C3H6-O]N-H, N=1à20, dont la représentation schématique est insérée Figure 1.
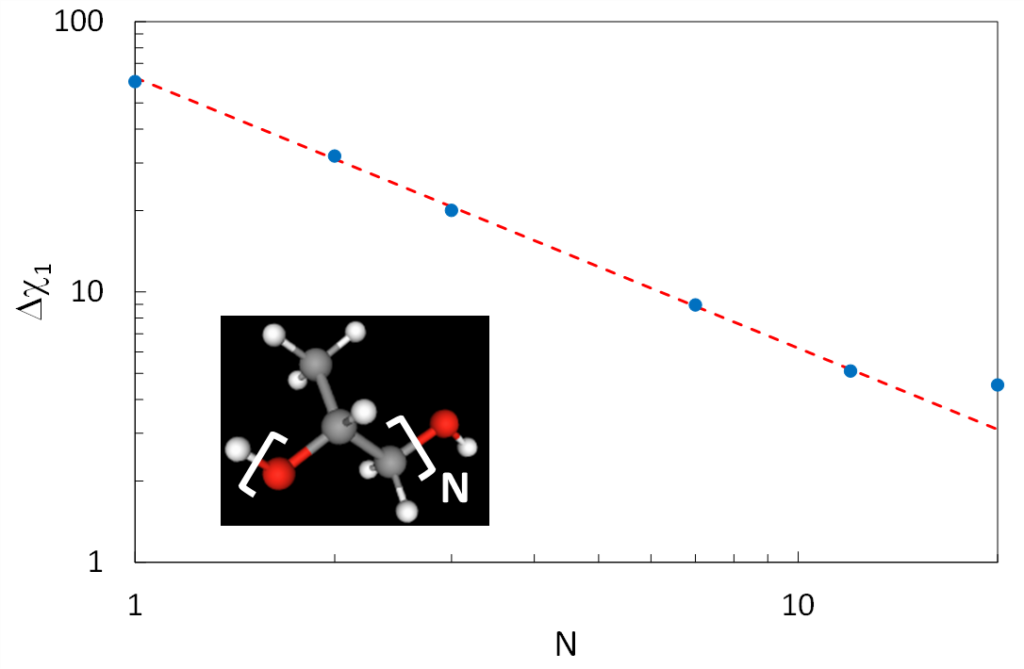
Le premier résultat surprenant vient de la susceptibilité diélectrique linéaire statique Dc1 qui, comme on peut le constater sur la Figure 1, évolue en 1/N. Cela indique que la réponse diélectrique linéaire des molécules provient uniquement des groupements -OH situés en bouts de chaîne, dont la concentration dans le matériau évolue en 1/N. Le reste de la molécule a donc une contribution négligeable, ce qui est contrintuitif car les unités chimiques qui composent le cœur de la chaîne possèdent des dipôles dont les valeurs sont comparables à celles des groupements -OH terminaux. Néanmoins, l’allongement de la molécule ne semble pas perturber les dipôles qui dominent la réponse diélectrique.
Le deuxième résultat, tout aussi inattendu, concerne l’évolution relative de Ncorr en fonction de ta, obtenue à partir des mesures non linéaires. En effet, les susceptibilités mesurées à l’ordre 3 présentent bien un pic, comme prédit par Bouchaud et Biroli (BB) [2], la hauteur du pic étant proportionnelle à Ncorr. La Figure 2(a) montre l’évolution relative de Ncorr(T) en fonction du temps de relaxation pour les N-PG mesurés, sur la gamme N=1à20. Lorsque ta augmente, la température diminue, on constate donc bien que lors du refroidissement, la taille des HD augmente, ce qui était attendu. Par contre, on remarque que quel que soit N, l’évolution relative de Ncorr en fonction de T est la même. Pour confirmer ce résultat, la Figure 2(b) est basée sur une autre méthode, indépendante de la première, permettant d’estimer la variation relative en température de Ncorr à partir des mesures linéaires. La conclusion est la même, l’évolution relative de la taille des HD est indépendante de la longueur de la molécule sur 4 décades de temps de relaxation, alors même que le fait que nous augmentions N d’un facteur 20 nous permet d’explorer de part et d’autre de la taille estimée pour ξ dans la littérature des hétérogénéités dynamiques.
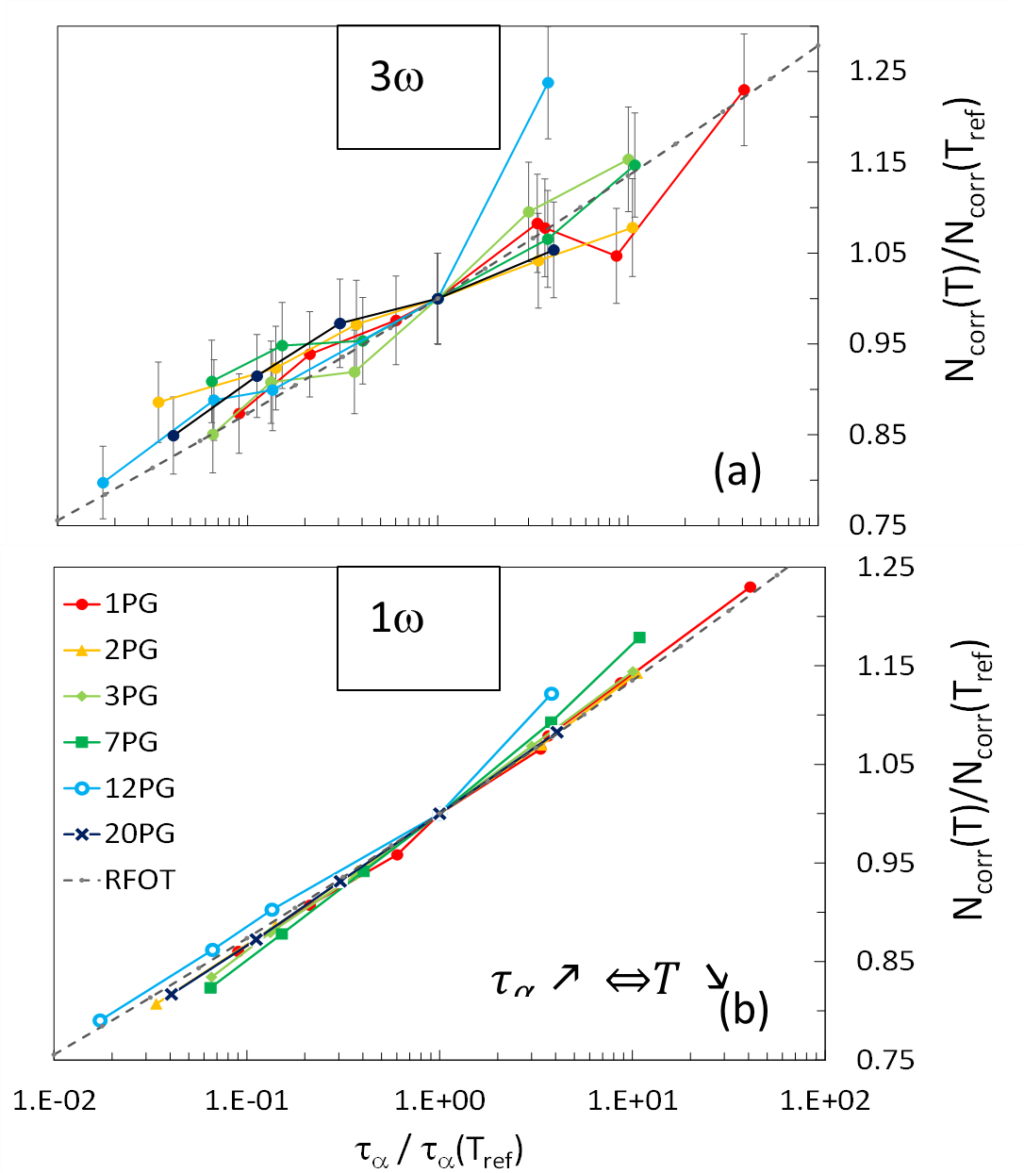
Enfin plusieurs théories ont été développées dans le but de modéliser la transition vitreuse. Parmi elles, nous citerons les deux principales [3] :
- Random First Order Transition theory (RFOT) : basée sur les premiers principes et inspirée d’un modèle à p-spin, cette théorie thermodynamique fait intervenir un paysage d’énergie libre contenant des puits d’énergie libre nécessitant un effet collectif des molécules pour relaxer
- Kinetically Constrained Models (KCM) : basés sur une hypothèse de thermodynamique triviale, leur paysage d’énergie libre est totalement plat et ne fait donc pas intervenir d’effet collectif dynamique.
Les résultats des mesures non linéaires montrent qu’un effet réellement collectif des molécules dans les HD est présent lors de la relaxation dynamique, puisque la susceptibilité à l’ordre 3 présente un pic – à fréquence finie – dont la hauteur diminue quand la température augmente. Il est ainsi démontré que KCM ne permet pas de reproduire les résultats expérimentaux, contrairement à RFOT qui est en bon accord avec les résultats.
Références :
[3] Voir références dans :
C. Raepsaet, C. Alba-Simionesco, C. Wiertel-Gasquet, and F. Ladieu, Nonlinear response in oligomers across chain lengths, Phys. Rev. Res. 7, 043244 (2025),
Contacts CEA : Caroline Raepsaet, François-Ladieu (SPEC/SPHYNX) et Christiane Alba-Simionesco (LLB/MMB).
Faits marquants antérieurs :
- « Interprétation par dynamique moléculaire de la réponse diélectrique d’un liquide surfondu près de la transition vitreuse » (2025)
- « La transition vitreuse : mise en évidence de son caractère critique à l’aide de réponses non linéaires » (2017)
- « Première mise en évidence de la transition vers l’ordre amorphe dans les verres » (2016)
- « La transition vitreuse : effets coopératifs et longueur dynamique » (2005)


