Les électrons plongés dans un champ magnétique décrivent des orbites circulaires, générant ainsi un moment magnétique qui s’oppose au champ magnétique. Cet effet donne lieu, dans sa version quantique, au diamagnétisme de Landau bien connu dans les matériaux conducteurs. On sait depuis longtemps que ce magnétisme orbital dépend de la structure, cristalline et électronique, du matériau considéré. Plus récemment, il a été démontré que lors du mouvement orbital des électrons, leur fonction d’onde, reflétant les symétries cristallines, acquiert un déphasage d’origine géométrique, dit phase de Berry, qui influe sur la direction de la réponse magnétique.
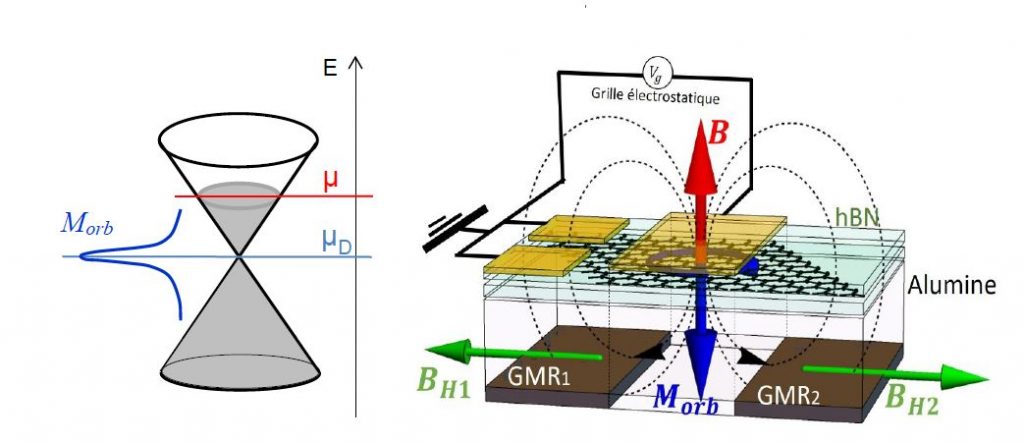
Dans le cas du graphène, la structure électronique présente un point remarquable, le point de Dirac, qui est à l’intersection de deux bandes d’énergie en forme de cônes et pour lequel les électrons se comportent comme si leur masse était nulle. En particulier, dès 1956, une réponse orbitale, diamagnétique et divergente, a été prédite lorsque le potentiel chimique coïncide avec l’énergie du point de Dirac, c’est-à-dire lorsque que la bande inférieure est complètement remplie d’électrons et la bande supérieure complètement vide (voir figure). Cette prédiction est surprenante, car c’est au point de Dirac que la densité d’électrons est minimale. Elle s’explique avec la phase de Berry qui vaut π dans le graphène et conduit à une réponse orbitale négative, s’opposant au champ magnétique et donc diamagnétique. De plus, cette phase intervient aussi dans la quantification des niveaux d’énergie de Landau et donne lieu à un niveau au point de Dirac, créant ainsi une densité d’états non nulle en ce point.
La première mise en évidence expérimentale de cette singularité magnétique vient d’être réalisée dans une collaboration menée par des physiciennes et des physiciens du Laboratoire de physique des solides à Orsay (LPS, CNRS/Université Paris-Saclay), grâce à une mesure ultrasensible de l’aimantation d’un cristal micrométrique de graphène quasiment parfait, et au contrôle de la densité d’électrons autour du point de Dirac avec un champ électrostatique. Cette étude est publiée dans la revue Science.
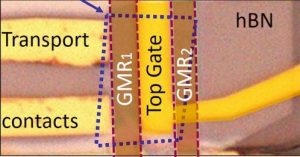
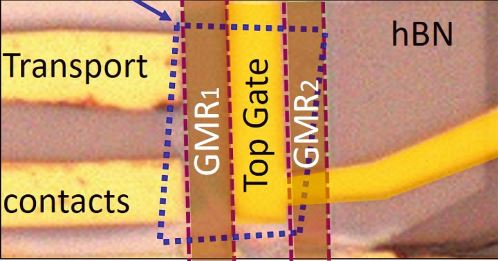
Le dispositif de mesure comprend une paire de capteurs à magnétorésistance géante (GMR) fabriqués au Service de physique de l’état condensé (SPEC, CEA/CNRS) qui ont la caractéristique d’être très sensibles au champ magnétique généré par les boucles de courant orbital induites dans le graphène, tout en étant insensibles au champ magnétique perpendiculaire au plan de graphène qui génère ces boucles (figure). Une tension électrostatique est appliquée à une électrode, la grille, placée au-dessus de l’échantillon. La grande sensibilité de la réponse magnétique du graphène à la tension de grille a été mise à profit en modulant celle-ci périodiquement en fonction du temps, et ainsi, grâce à la détection synchrone du signal GMR, une discrimination optimale du signal magnétique recherché par rapport aux bruits parasites de l’expérience est obtenue : la précision est alors meilleure que le millionième du champ magnétique terrestre.
En balayant le potentiel chimique autour du point de Dirac grâce à la tension de grille, un pic diamagnétique est alors détecté au point de Dirac, en accord avec la théorie. Lorsque le champ magnétique augmente, sa largeur augmente et des oscillations périodiques apparaissent de part et d’autre du point de Dirac, connues sous le nom d’oscillations de Haas-van Alphen, et qui sont les signatures des autres niveaux d’énergie de Landau.
Ces résultats ouvrent tout un champ d’investigation des courants orbitaux dans le graphène et dans les matériaux topologiques bidimensionnels. Ils offrent un nouvel outil pour y explorer des états électroniques corrélés générés par l’effet combiné des interactions coulombiennes, des contraintes et des potentiels de moiré.
Référence :
« Detection of graphene’s divergent orbital diamagnetism at the Dirac point »
J. Vallejo, N.J. Wu, C. Fermon, M. Pannetier-Lecoeur, T. Wakamura, K. Watanabe, T. Tanigushi, T.Pellegrin, A. Bernard, S. Daddinounou, V. Bouchiat, S. Guéron, M. Ferrier, G. Montambaux et H. Bouchiat. Science 374 6573 (2021) 1399
Voir l'actualité sur le site du CNRS/InP : « Des courants bien singuliers dans le graphène« .
Contacts CEA-Iramis : Claude Fermon et Myriam Pannetier-Lecoeur (SPEC/LNO)
Collaboration :
- Université Paris-Saclay, CNRS, Laboratoire de Physique des Solides, 91405 Orsay, France.
- Laboratoire Nano-Magnétisme et Oxydes SPEC/LNO, CEA, CNRS, Université Paris-Saclay, 91191 Gif-sur-Yvette, France.
- Research Center for Functional Materials, National Institute for Materials Science, 1-1 Namiki, Tsukuba 305-0044, Japan.
- Néel Institute, CNRS, 38000 Grenoble, France.