Depuis 2015 les chercheurs du groupe Quantronique du SPEC (IRAMIS), au sein d’une collaboration avec des chercheurs de UCL à Londres et de l’université de Aarhus au Danemark, appliquent les techniques des circuits supraconducteurs quantiques refroidis à ultra-basse température (10 millikelvins) à la résonance magnétique. En particulier les spins électroniques sont couplés à un résonateur supraconducteur fabriqué à la surface de l’échantillon dont les dimensions transverses du fil servant d’inductance (cf figure 2) sont de l’ordre de quelques micromètres afin de confiner le champ micro-onde et d’exalter l’interaction avec les spins. Les premiers résultats obtenus en 2016 avaient montré une sensibilité record de 1700 spins détectables avec un rapport signal-à-bruit de 1 en 1 seconde d’intégration [1]. Dans cette expérience, les très basses températures nous permettaient de supprimer complètement la composante thermique du bruit, mais il restait les fluctuations quantiques du champ micro-onde dans son état fondamental (le vide).
En 2017 les chercheurs ont amélioré ces résultats en réalisant deux expériences différentes.
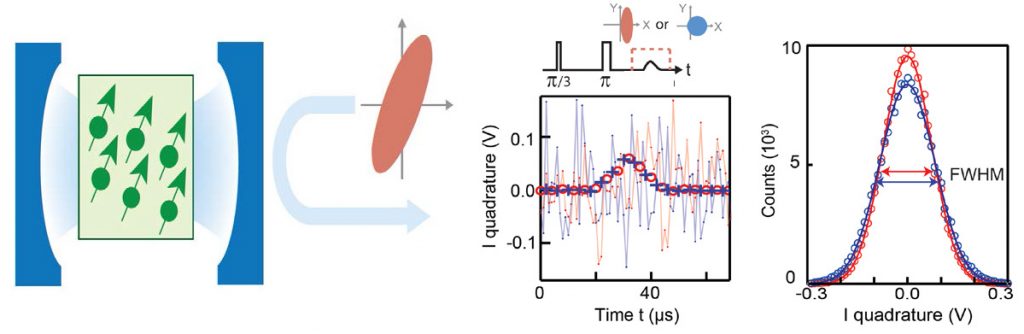
Dans une première expérience (figure 1), ils ont trouvé le moyen de réduire le bruit du spectromètre encore en-dessous des fluctuations quantiques du vide [2]. Si le principe d’incertitude de Heisenberg limite l’incertitude combinée de deux variables dites conjuguées, il n’interdit pas de fabriquer des états dans lesquels l’incertitude d’une variable est réduite aux dépens de l’autre. Ces états sont appelés « états comprimés » et ils fournissent une méthode pour effectuer des mesures qui vont au-delà de la limite des fluctuations quantiques du vide. Dans l’expérience un amplificateur paramétrique Josephson génère un état comprimé du champ micro-onde qui est ensuite envoyé à l’entrée du spectromètre (voir figure 1). Dans cet état, les fluctuations qui sont en phase avec le signal émis par les spins électroniques que nous cherchons à détecter sont réduites, alors que le bruit en quadrature de phase est lui amplifié. Du coup le rapport signal-à-bruit de la mesure des spins est amélioré de 1.2 dB comme on peut le voir sur la figure 1. Malgré la relativement modeste amélioration du rapport signal-à-bruit apporté par les états comprimés, ce résultat est marquant d’un point de vue fondamental puisqu’il s’agit de la première application d’états non-classiques du champ électromagnétique au domaine de la résonance magnétique.
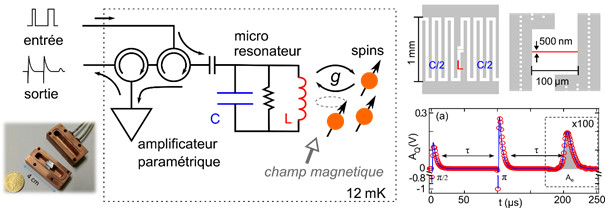
Dans une seconde expérience (figure 2), les chercheurs ont optimisé le design du circuit supraconducteur, en réduisant ses dimensions transverses en-dessous d’un micromètre (avec une inductance de largeur 500nm). Cela leur a permis d’améliorer la sensibilité encore d’un ordre de grandeur [3], atteignant une sensibilité suffisante pour détecter 65 spins en une seconde d’intégration qui constitue le record actuel de la résonance magnétique à détection inductive. Cette sensibilité est suffisante pour envisager des applications nouvelles en biochimie, par exemple mesurer le signal de résonance magnétique provenant d’une cellule unique. Et puis, encore un petit effort, et la détection d’un unique spin semble à portée de main.
Références :
[1] Reaching the quantum limit of sensitivity in electron spin resonance
A. Bienfait, J. J. Pla, Y. Kubo, M. Stern, X. Zhou, C. C. Lo, C. D. Weis, T. Schenkel, M.L.W. Thewalt, D. Vion, D. Esteve, B. Julsgaard, K. Moelmer, J.J.L. Morton, P. Bertet, Nature Nanotechnology 11, 253 (2016).
[2] Magnetic Resonance with Squeezed Microwaves
A. Bienfait, P. Campagne-Ibarcq, A.H. Kiilerich, X. Zhou, S. Probst, J. J. Pla, T. Schenkel, D. Vion, D. Esteve, J.J.L. Morton, K. Moelmer, P. Bertet, Phys. Rev. X 7, 041011 (2017).
[3] Inductive-detection electron-spin resonance spectroscopy with 65 spins/√Hz sensitivity
S. Probst, A. Bienfait, P. Campagne-Ibarcq, J.J. Pla, B. Albanese, J.F. Da Silva Barbosa, T. Schenkel, D. Vion, D. Esteve, K. Moelmer, J.J.L. Morton, R. Heeres, P. Bertet, Appl. Phys. Lett. 111, 202604 (2017).
Contact CEA : Patrice Bertet – SPEC/Quantronique


