La résonance magnétique nucléaire (RMN) est une technique d'analyse puissante mais peu sensible. Des enjeux majeurs en analyse chimique (détection de produits en très faibles concentrations ou étude des effets isotopiques, notamment) incitent à rechercher de nouvelles méthodes pour détecter et séparer les signaux faibles des composantes principales du signal.
Pour ceci, une approche existe : au lieu d'appliquer une impulsion radiofréquence pour exciter le système, il est possible d'analyser l'autocorrélation du bruit du signal aux bornes de la bobine radiofréquence de détection RMN, qui est, par construction, fortement couplée avec les spins de l'échantillon à analyser. Dans le cadre d'un travail collaboratif avec une équipe de l'Université Johannes Kepler de Linz (Autriche), financée par une subvention conjointe ANR-FWF, une nouvelle théorie générale de ce type de détection a pu être établie, et montre la forte amélioration de sensibilité permise par la technique.
De plus, l'existence d'une signature spectrale due à l'inhomogénéité du champ magnétique statique est démontrée et elle fournit aussi une référence pour le déplacement chimique, non affectée par le couplage non linéaire entre l'aimantation de l'échantillon et la bobine de détection. Cette capacité de détection améliorée a pu être appliquée aux mesures d'effets isotopiques secondaires [1].

La procédure usuelle pour une mesure RMN consiste à polariser les spins nucléaires de la matière à étudier, à l'aide d'un champ magnétique statique généralement intense (quelques Teslas), puis à exciter l'aimantation nucléaire obtenue par une impulsion radiofréquence. Le signal mesuré est créé par la précession de Larmor de cette aimantation autour de la direction du champ statique lors de son retour à l'équilibre. Le signal est maximal quand il y a accord entre la fréquence de précession des spins et la fréquence de résonance variable du circuit électronique de détection, incluant la bobine entourant l'échantillon. Le signal RMN présente ainsi des résonances pour chaque élément disposant d'un spin. A noter que l'impulsion excitatrice est une perturbation non négligeable du système de spins.
Une seconde méthode de mesure RMN, moins perturbatrice et permettant une meilleure analyse de l'environnement chimique, consiste à simplement analyser le bruit du signal RMN, sans impulsion excitatrice cohérente préalable. Par exemple, de simples fluctuations de courant dans la bobine, génèrent un champ radiofréquence qui perturbe très légèrement l’aimantation, dont la relaxation excite en retour la bobine, créant ainsi une rétroaction non-linéaire. Ce terme non linéaire est en mesure de coupler la dynamique des spins des différentes espèces.
Plusieurs sources de bruit incohérentes sont en mesure de créer un tel signal RMN :
- les fluctuations d’origine quantique de l'aimantation transverse
- la résistance de la bobine de mesure [2]
- l’impédance d'entrée du préamplificateur [3,4]
Étant issu de la rétroaction entre la bobine et le système, le signal, très faible, peut être avantageusement extrait par une mesure de corrélation sur le bruit mesuré aux bornes du détecteur : le calcul de la densité spectrale de puissance du signal (ou de façon équivalente la transformée de Fourier de sa fonction d'autocorrélation) donne le spectre.
Les spectres obtenus présentent les résonances attendues, mais aussi une assemblée de pics peu intenses mais très bien résolus dont l'origine est resté longtemps mystérieuse. Pour interpréter ces spectres, une nouvelle méthode de calcul est alors introduite, incluant l'ensemble des différentes sources de bruit (spins, résistance de la bobine, et impédance d'entrée du préamplificateur) et la possible présence de différentes espèces de spin, pour en dériver une solution analytique. Le calcul des densités spectrales résultantes est basé sur une dynamique des spins en champ aléatoire. Il faut aussi noter que le spectre obtenu est fortement altéré par l’emploi de faibles températures de bobine (une vingtaine de Kelvins) comme employées usuellement.
La solution générale obtenue permet aussi de traiter le cas d'une inhomogénéité du champ magnétique statique : un tel gradient induit une petite discontinuité dans le spectre, centrée à la valeur de son déplacement chimique exact, sans être affectée par le décalage de fréquence induit par le champ de rétroaction.

– À gauche : par la méthode RMN usuelle, après excitation cohérente radiofréquence. Les contributions secondaires sont pratiquement indétectables. Le couplage avec la bobine induit un élargissement et un déplacement de la raie principale.
– À droite : les différentes composantes dans le spectre de bruit de spin, selon le modèle analytique développé. La courbe en noir donne la somme des contributions dues aux fluctuations des spins et de courant lié à la résistance de la bobine (contributions usuellement considérées), en bleu celle résultant de l'impédance d'entrée du préamplificateur (prise en compte pour la première fois dans un modèle analytique) et en rouge le signal observé par la combinaison des deux. Celle-ci montre sans ambiguïté des pics fins et bien résolus dus aux composantes minoritaires.
Ce modèle a été utilisé pour interpréter le spectre RMN du proton (H) issu d'une solution d'acétonitrile. Il permet d'attribuer sans ambiguïté les plus fines composantes observées à la présence de l'isotope 13C du carbone (abondance naturelle ~1 %). Ces isotopes induisent une concentration relative de 0.5% pourt chaque pic. Le spectre global montre une raie principale large (12CH3–12CN) et deux pics fins décalés de +66,2 et -69,7 Hz, attribués aux protons au sein des groupements méthyl 13CH3. Il permet ensuite de détecter les protons au sein de la molécule 12CH3–13CN, pour lesquels le décalage isotopique secondaire est de +4,3 et -5,7 Hz par rapport à la fréquence de résonance centrale repérée par la petite discontinuité liée à l'inhomogénéité du champ. Celle-ci, située à la valeur du déplacement chimique exact (i.e. non affectée par la rétroaction de la bobine) donne une référence absolue pour le spectre en fréquence.

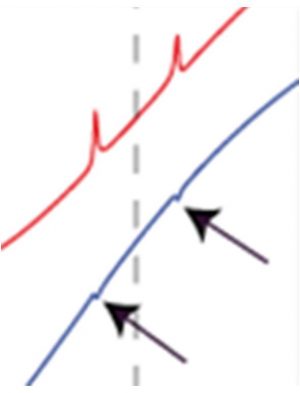
À droite : détail de la partie centrale du spectre, montrant les contributions des effets isotopiques secondaires du 13CN. Le faible pic central, donnant le décalage chimique exact, est dû à l'inhomogénéité résiduelle du champ polarisant.
Ce travail de développement d'un modèle complet de spectroscopie RMN de bruit de spins montre donc pour la première fois qu'il est possible d'interpréter les détails les plus fins des spectres obtenus. La méthode présente de nombreux avantages, puisqu'elle simplifie le dispositif de mesure (plus d'impulsion RF) et évite la perturbation du système étudié. Une nouvelle spectroscopie de « bruit de spin' devient ainsi possible.
Plusieurs autres perspectives sont aussi ouvertes :
- le modèle analytique obtenu, capable de prendre complètement en compte les effets du préamplificateur et de la ligne de transmission, doit permettre d'optimiser les sondes RMN aussi bien pour la méthode usuelle avec excitation par impulsions RF, que pour la présente méthode de mesure par bruit de spins.
- Pour la RMN usuelle, la détermination directe du décalage absolu en fréquence est possible en tirant profit de la réponse non linéaire en présence de gradient. Ceci permet alors la saturation RF précise des signaux de solvant. En retour, il est ainsi possible d'évaluer précisément l'homogénéité du champ magnétique statique.
- À plus long terme, la méthode ouvre la voie à de nouveaux schémas de détection avec des dispositifs électroniques simplifiés (circuit de réception seul) qui pourront être utiles dans le développement de « laboratoire sur puces » (Lab-on-chip), où l'analyse de très petites quantités de matière dans un petit volume est requise.
Références :
| 1] Nonlinear detection of secondary isotopic chemical shifts in NMR through spin noise. M. T. Pöschko1, V. V. Rodin1, J. Schlagnitweit1, N. Müller1, H. Desvaux2*, Nat. Commun. 7, 13914 (2016). |
 |
[2] Nuclear spin noise at room temperature
M.A. McCoy and R.R. Ernst, Chem. Phys. Lett. 159, 587-593 (1989).
[3] Nuclear spin noise in NMR revisited
G. Ferrand, G. Huber, M. Luong, and H. Desvaux, J. Chem. Phys. 143, 094201 (2015).
[4] On the tuning of high resolution NMR probes
M. T. Pöschko, J. Schlagnitweit, G. Huber, M. Nausner, M. Hornicakova, H. Desvaux, and N. Müller, ChemPhysChem 15, 3639-3645 (2014). (highlighted in SpectroscopyNow).
Voir aussi : « Vers des seuils de sensibilité record pour la RMN, par la mesure de 'bruit de spins hyperpolarisés« .
Article (en allemand) du Tiroler Tageszeitung Onlineausgabe : Linzer Forscher detektieren winzige chemische Signale.
Contact CEA : H. Desvaux, NIMBE/LSDRM.
Collaboration :
- Institute of Organic Chemistry, Johannes Kepler University Linz, Altenbergerstraße 69, 4040 Linz, Austria
-
CEA – NIMBE/Laboratoire Structure et Dynamique par Résonance Magnétique (LSDRM),
UMR CEA-CNRS 3685, CEA/Saclay, 91191 Gif-sur-Yvette, France.