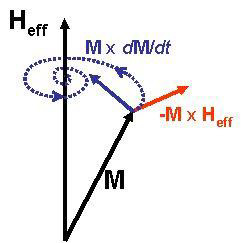Modélisation de la dynamique de spin par calcul de structure électronique.

Le magnétisme des matériaux est essentiellement gouverné par le spin des électrons et leur interaction mutuelle. L’ordre magnétique qui en résulte est piloté par l’interaction d’échange qui couple deux sites i et j du matériau par une énergie de la forme

. Une intégrale d’échange J_ij positive favorise un ordre ferromagnétique (avec des aimantations toutes alignées dans un même sens), tandis qu’une intégrale négative favorisera un ordre antiferromagnétique (avec une orientation alternée des spins et une aimantation globale nulle). Cet ordre magnétique peut-être brisé dès que la température du matériau dépasse une certaine température, ou lorsqu’une perturbation extérieure (comme un champ électromagnétique oscillant) est appliquée. Des magnons (ondes de spin stationnaires ou propagatives) vont alors se former dans le matériau. Au-delà de la température de transition de Curie (ordre ferromagnétique → paramagnétique) ou la température de transition de Néel (antiferro → paramagnétique), tout ordre magnétique collectif disparait et l’aimantation macroscopique devient nulle.

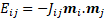
Pour déterminer les propriétés magnétiques de ces matériaux, il est donc primordial de décrire correctement ces différentes ondes de spin. L’approche la plus directe consiste à résoudre la dynamique de chacun des spins. Cette dynamique a été décrite pour la première fois par Larmor pour reproduire la précession d’un moment magnétique atomique m dans une induction externe constante B₀ :

Ici, la pulsation du mouvement de précession est proportionnelle à l’induction magnétique B₀. La constante de proportionalité γ est le rapport gyromagnétique. L’équation (1) a ensuite été généralisée par Landau et Lifshitz au cas d’un matériau magnétique pour lequel l’induction magnétique B₀ est remplacée par l’induction effective du matériau B_eff. m désignant l’aimantation macroscopique, l’induction effective s’exprime comme la dérivée fonctionnelle de l’énergie interne du matériau par rapport à cette aimantation, soit :

Cette équation très générale peut-être appliquée à un ensemble quelconque de moments magnétiques

en interaction via une fonctionnelle

. On obtient alors une série d’équations couplées :

Outre des aspects numériques délicats pour intégrer ces équations avec une précision suffisante, on doit maintenant déterminer l’interaction effective entre tous les moments magnétiques. Lorsque le matériau magnétique peut être décrit par une somme de termes de paires de moments magnétiques (modèle de Heisenberg), la fonctionnelle E s’écrit:

et l’expression du champ effectif est suffisamment simple pour que la précession des moments puisse être suivie sur des systèmes de grande taille et pour des temps longs.

Il peut s’avérer parfois très compliqué de déterminer précisément la valeur des intégrales d’échange et la validité du modèle d’Heisenberg n’est pas toujours assurée. En effet, pour des matériaux comme le fer, le cobalt, le chrome et leurs alliages, où le magnétisme y est plus “itinérant”, les interactions d’échanges sont extrêmement sensibles aux variations de configuration atomique, ainsi qu’à ses symétries et aux distances interatomiques. Par exemple les “J” d’un petit agrégat d’un composé seront très différents de ceux du même matériau à l’état massif ou de sa surface. De plus la validité du modèle d’Heisenberg s’en trouve limité autour d’états magnétiques proche de l’équilibre.

Par conséquent nous avons développé une approche qui s’affranchit de ces problèmes en décrivant l’énergie du système à l’aide d’un modèle de “liaisons fortes” décrivant précisément la structure électronique et magnétique du matériau. Elle permet d’explorer toutes les configurations magnétiques sans limitation de validité à l’aide de techniques de “pénalisation”. Le modèle énergétique en revanche est beaucoup plus compliqué et ne fournit pas une formule simple comme l’équation (3) permettant d’écrire analytiquement le champ effectif. Cependant, la méthode de pénalisation utilisée donne accès à l’induction effective et permet de résoudre le système d’équations (2).

Configuration magnétique initiale d’un icosaèdre de fer (l’aimantation des atomes autour de l’axe pentagonal forment un angle de 10° par rapport à cet axe) et son évolution temporelle calculée à l’aide du code DyNaMol.

Même si le principe de cette approche avait été décrit dans la littérature [1], elle n’avait jusqu’à présent jamais été implémentée. Nous l’avons mis en œuvre au sein du code DyNaMol et appliqué aux cas de petits agrégats magnétiques [2]. Cela permet d’une part de valider l'approche en la comparant au modèle d’Heisenberg dans des configurations où ce modèle s’applique, et d’autre part de mettre clairement en évidence les limites de ce modèle. Il est en effet possible d'en déduire les intégrales d’échange effectives et d'évaluer ainsi qu’elles ne changeaient pas lorsque les ondes de spins ont une fréquence faible.

L'étude se poursuit par celle d'agrégats magnétiques plus complexes; pour lesquels il est nécessaire d’étendre le modèle pour aborder une dynamique de spin couplée à la dynamique du réseau cristallin. Plusieurs travaux [3,4] ont déjà abordé ce problème complexe dans le cadre du modèle d’Heisenberg où les intégrales d’échange dépendent explicitement de la distance interatomique, ce qui le rend difficile (voir impossible) à paramétrer. Notre modèle de liaisons fortes ayant prouvé sa très bonne transférabilité, il constitue un cadre idéal pour modéliser tous les phénomènes couplant magnétisme et réseau, essentiels pour décrire la physique des alliages magnétiques.

Ces travaux ont été effectués dans le cadre du projet CEA bottom-up DyNaMol et ptc-simulation DyNaMol2.

Contacts CEA : Pascal Thibaudeau (DAM), Chu-Chun Fu (DES), Cyrille Barreteau (DRF/Iramis/SPEC/GMT) et Ramon Cardias (DRF/Iramis/SPEC/GMT).

Références :

[1] Equation of motion and the constraining field in ab initio spin dynamics, Simon Streib, Vladislav Borisov, Manuel Pereiro, Anders Bergman, Erik Sjöqvist, Anna Delin, Olle Eriksson, and Danny Thonig, Phys. Rev. B 102, 214407 (2020).

[2] Spin dynamics from a constrained magnetic tight-binding model, Ramon Cardias, Cyrille Barreteau, Pascal Thibaudeau, and Chu Chun Fu, Phys. Rev. B 103, 235436 (2021).

[3] Anisotropic magnetic molecular dynamics of cobalt nanowires, David Beaujouan, Pascal Thibaudeau and Cyrille Barreteau, Phys. Rev. B 86 174409 (2012).

[4] Massively parallel symplectic algorithm for coupled magnetic spin dynamics and molecular dynamics, Julien Tranchida Steve Plimpton, Pascal Thibaudeau and Aidan Thompson, J. Comp. Phys. 372, 406-425 (2018).