C. Janvier, L. Tosi, L. Bretheau, P. Senat, P.F. Orfila, Ç. Ö. Girit, M. Stern, P. Bertet, P. Joyez, D. Vion, D. Esteve, M. F. Goffman, H. Pothier, C. Urbina, Groupe Quantronique
Localisés dans tout lien faible entre deux éléments supraconducteurs, des états électroniques bien spécifiques, appelés états d’Andreev, sont présents au sein du gap supraconducteur. Ces états sont observés par exemple dans les expériences réalisées avec des contacts à un seul atome entre deux électrodes supraconductrices. Par un dispositif original, où la boucle supraconductrice et son lien faible sont couplés à un résonateur microonde, il est possible d'exciter et suivre les populations dans une superposition de ces états. L'observation des oscillations de Rabi entre l'état fondamental et le premier état excité d'Andreev, ainsi que la mesure du temps de cohérence du système apportent la démonstration que le système constitue un nouveau type de qubit supraconducteur.
Les états d’Andreev
Les états d’Andreev apparaissent dans les supraconducteurs inhomogènes : dans un vortex, à proximité d’une impureté magnétique, ou dans un lien faible entre deux supraconducteurs. Dans ces situations, la phase du supraconducteur, propriété macroscopique de la fonction d’onde qui décrit l’état quantique de tous les électrons de conduction, varie alors en fonction de la position. Cette inhomogénéité de la phase conduit à une frustration de la supraconductivité et les électrons au niveau de Fermi gagnent une énergie inférieure au gap supraconducteur Δ lors de la transition supraconductrice. On obtient des états localisés, appelés états d’Andreev. L’excitation d’énergie minimale correspond à une énergie inférieure à 2D, qui est l’énergie minimale pour casser une paire dans un supraconducteur homogène (1,2). Le cas le plus simple est celui d’un lien faible très court, qu’on obtient dans nos expériences en fabriquant un contact à un atome entre deux électrodes supraconductrices formant une boucle (Fig. 1). La différence de phase entre les supraconducteurs de part et d’autre du contact est contrôlée en appliquant un flux magnétique dans la boucle. Le nombre maximum d’états d’Andreev dépend uniquement du nombre de canaux de conduction, qu’on arrive à réduire à essentiellement un seul dans un contact à un atome. En excitant avec un photon microonde l’état d’Andreev depuis son état fondamental |g> (ground state), on accède à un autre état localisé |e> (excited state).
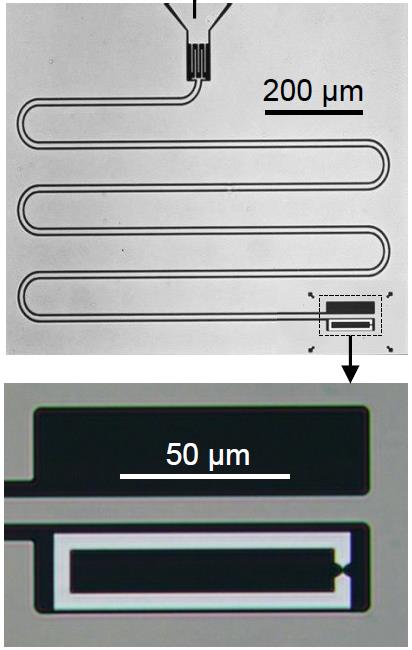
Figure 1: Résonateur microonde couplé à une boucle supraconductrice comprenant un contact atomique. La micrographie du haut montre le résonateur, terminé à une extrémité par une capacité interdigitée, à l’autre par un court-circuit. En bas, zoom sur la région du court-circuit, où est placée la boucle supraconductrice (en blanc). La boucle a une constriction à droite, qui permet d’obtenir un contact à un atome en pliant le circuit et en s’arrêtant juste avant la cassure.
Un contact atomique en géométrie “circuit-QED”
Nos expériences (3,4) sondent les propriétés de superpositions quantiques de ces deux états avec les techniques de la “circuit-QED”, l’électrodynamique quantique des circuits. C’est l’équivalent avec des atomes artificiels de l’électrodynamique quantique en cavité utilisée en physique atomique, notamment dans le groupe de S. Haroche, J.-M. Raimond et M. Brune au LKB à Paris. En couplant un système quantique à des photons dans un résonateur, on arrive à la fois à l’isoler de manière optimale et à le manipuler avec des impulsions électromagnétiques. Le résonateur microonde que nous utilisons est montré sur la Fig. 1 : c’est une ligne coplanaire dont la longueur correspond à un quart de longueur d’onde à 10 GHz. A une extrémité, il est court-circuité, et le courant qui le traverse crée un flux dans la boucle supraconductrice incluant le contact atomique, ce qui induit un couplage avec les états d’Andreev. A l’autre extrémité, il se termine par une capacité qui est comme un miroir partiellement transparent. Le coefficient de réflexion des microondes incidentes sur la cavité près de sa fréquence de résonance est différent dans l'état |g> et l'état |e> ce qui permet de sonder l'état d'Andreev. A travers la capacité, on envoie également des impulsions microondes à la fréquence de transition entre les états |g> et |e> afin de créer des superpositions.
Manipulation cohérente
La Figure 2 montre des oscillations de Rabi obtenues en appliquant des impulsions microonde de durée croissante, qui créent des superpositions a|g>+b|e>. La probabilité de mesurer l’état |g> est |a|², celle de mesurer l’état |e> est |b|². La variation des populations observées dans les deux états en répétant la mesure quelques milliers de fois montre les oscillations cohérentes de leurs poids respectifs dans la superposition.
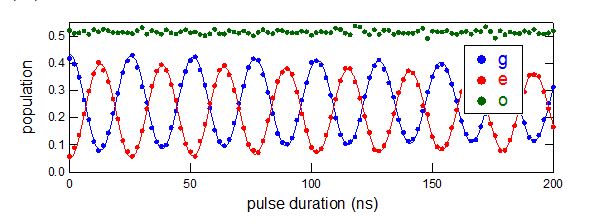
Figure 2 Oscillations de Rabi montrant la mesure de superpositions d’états créées en appliquant une impulsion microonde à la fréquence de transition entre les états |g> et |e>. Suivant la durée de l’impulsion (axe inférieur), le poids des états |g> et |e> varie de manière sinusoïdale. On observe aussi une fois sur deux un état “impair |o>, qu’on ne discutera pas ici.
A partir de l’observation des oscillations de Rabi, nous avons sondé le temps de vie de l’état |e> (de l’ordre d’1 µs) et le temps de cohérence des superpositions d’états (de l’ordre de 0.2 µs), voir Figure 3. Des expériences pour comprendre les mécanismes de décohérence sont en cours.
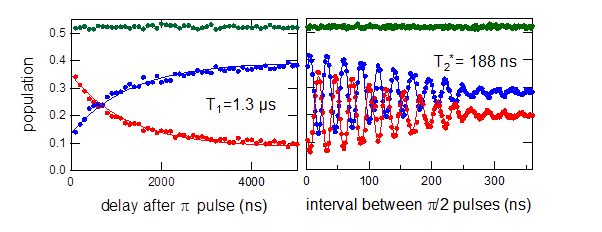
Figure 3 A gauche : Mesure du temps de vie T1 de l’état excité, en faisant varier le délai entre un pulse p qui échange les populations de |g> et |e> et la mesure de l’état. A droite : Mesure du temps de cohérence T2* de superpositions d’états (franges de Ramsey) : un premier pulse π/2 prépare une superposition de |g> et |e>. La phase de cette superposition varie librement pendant l’intervalle de temps avant un deuxième pulse p/2. L’atténuation du signal est due à la décohérence pendant la période d’évolution libre. La signification des couleurs est la même que dans Fig. 2.
Conclusion : un nouveau qubit supraconducteur ?
Nos résultats démontrent qu’il est possible d’accéder à des états microscopiques inhérents aux supraconducteurs, et que ces états présentent de la cohérence quantique. Il a été proposé d’utiliser la cohérence (jusqu’ici supposée) des états d’Andreev pour les utiliser comme qubits supraconducteurs d’un type nouveau, puisqu’ils reposent non pas sur des modes électromagnétiques, mais sur des états microscopiques (5,6). Cette expérience en démontre le principe, même s'il semble difficile aujourd'hui d’envisager une architecture de processeur quantique à base de simples contacts atomiques.
Références :
| 1. Exciting Andreev pairs in a superconducting atomic contact, L. Bretheau, Ç. Ö. Girit, H. Pothier, D. Esteve, & C. Urbina, Nature 499 312 (2013). |
|
| 2. Supercurrent spectroscopy of Andreev states L. Bretheau, Ç. Ö. Girit, C. Urbina, D. Esteve, and H. Pothier, Phys. Rev. X 3, 041034 (2013). |
|
| 3. Superconducting atomic contacts inductively coupled to a microwave resonator, C Janvier, L Tosi, Ç Ö Girit, M F Goffman, H Pothier and C Urbina, J. Phys.: Condens. Matter 26, 474208 (2014). |
|
| 4. Coherent manipulation of Andreev states in superconducting atomic contacts, preprint C. Janvier, L. Tosi, L. Bretheau, Ç. Ö. Girit, M. Stern, P. Bertet, P. Joyez, D. Vion, D. Esteve, M. F. Goffman, H. Pothier, & C. Urbina, Science 349 (2015) 1199. |
 |
| 5. Andreev level Qubit, A. Zazunov, V. S. Shumeiko, E. N. Bratus’, J. Lantz, & G. Wendin, Andreev Level Qubit, Phys. Rev. Lett.90, 087003 (2003). |
|
| 6. Andreev quantum dots for spin manipulation, N. M. Chtchelkatchev and Y.. V. Nazarov, Phys. Rev. Lett.90, 226806 (2003). |
Contact IRAMIS : Cristian Urbina (SPEC- Groupe Quantronique).




