Première mise en évidence de la transition vers l’ordre amorphe dans les verres

Les verres forment l’essentiel de nos matériaux du quotidien, et prennent une place croissante dans les technologies modernes (fibres optiques, etc…). Pourtant leur mécanisme de formation reste une énigme : certaines théories décrivent les verres comme de simples liquides hyper visqueux ; d’autres en revanche affirment que ce sont de vrais solides, avec un ordre thermodynamique sous-jacent très subtil appelé “ordre amorphe”, auquel correspond une minimisation locale de l'énergie.

Notre collaboration entre quatre laboratoires vient de montrer que l’on peut trancher cette controverse par des mesures de susceptibilités électriques non linéaires du 3^ème et du 5^ème ordre [1]. En réalisant ces expériences, qui sont une première du genre, on montre qu'un ordre amorphe existe bien dans les verres. La transition entre l'état liquide et l'état vitreux correspond à une nouvelle classe d’universalité de phénomènes critiques, où les domaines amorphes qui s'ordonnent sont compacts.

Liquide ultra visqueux ou vrai solide ? Une réelle controverse existe entre ces deux visions d'un verre, et ceci pour une raison simple : si un ordre amorphe existe, il se développe pour former des domaines avec une taille caractéristique L, qui doit en théorie croitre logarithmiquement avec le temps t_a de relaxation du système. Ainsi, pour atteindre un régime où L serait vraiment grand (> 10 a, “a” étant la taille élémentaire moléculaire), le temps de mise à l’équilibre doit être supérieur à l’âge de l’univers. Sur des temps expérimentalement accessibles, L ne peut donc pas devenir très supérieur à a, et les observations structurales restent peu discriminantes entre un scénario où L/a reste fixé à 1 (liquide ultra visqueux), et un scénario où un ordre amorphe s'installe, pour lequel L/a n'augmente que de quelques unités quand la température s'approche du point critique.

Notre idée centrale pour contourner cette difficulté est d’utiliser une propriété peu utilisée, mais pourtant générale, des phénomènes critiques : si un ordre se développe quand on approche de la température critique, alors, la réponse (ou susceptibilité) à l'application d'un champ extérieur E (par exemple un champ électrique) diverge avec L à tous les ordres, et ceci de façon plus rapide pour les réponses non linéaires d'ordre élevé (χ_2m+1 E^2m+1 , m entier et > 1), que pour la réponse linéaire χ₁E (les susceptibilités d’ordre pair χ_2m étant nulles par symétrie, voir [2]). Montrer alors que χ_2m+1 se comporte comme une puissance de χ₁ est en fait un test de criticalité aussi puissant que de montrer la divergence de χ₁ quand l’ordre s’établit sur des grandes distances à l'approche du point critique. Nous avons donc cherché à comparer les diverses susceptibilités χ_2m+1 entre elles sur la gamme de température où le temps de relaxation est expérimentalement mesurable.

[i] Il faut noter que les susceptibilités d’ordre pair c_2m sont nulles par raison de symétrie, voir [2].

Le comportement de la susceptibilité électrique, à l’ordre 3 et 5, montre que les structures en domaines amorphes dans un verre et un liquide visqueux sont bien distinctes et séparées par une transition de phase thermodynamique structurale. Les courbes montrent le résultat principal de la mesure : le comportement à l’approche de la transition vitreuse, de χ5 en fonction de la fréquence du champ électrique appliqué et de la température. (pour un liquide les courbes seraient plates). © Peter Lunkenheimer – Univ. Augsburg.

Le cas des verres est cependant spécifique, car on montre que pour un ordre amorphe χ₁ ne comporte pas d’information structurale [2], et la première susceptibilité utile est χ₃. Il nous faut donc comparer χ₃ et χ₅. La difficulté vient alors de l’extrême faiblesse des signaux à détecter, puisqu’en pratique la réponse χ₅ E⁵ est plusieurs ordres de grandeur inférieure à χ₃ E³, qui est elle-même plusieurs ordres de grandeur inférieure à la réponse linéaire χ₁E.

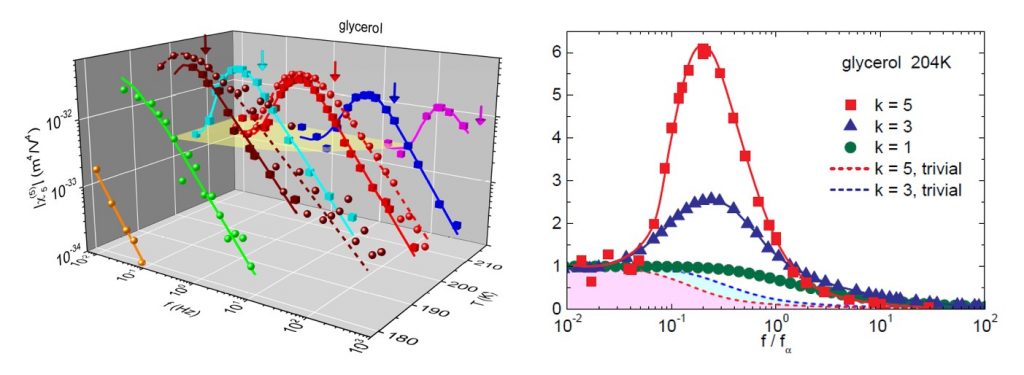
La difficile mesure de χ₃ n'a été réalisée que récemment et dans seulement quelques laboratoires [2, 3], la mesure de χ₅, restait à faire. Notre collaboration a utilisé, en parallèle, deux expériences optimisées selon deux axes distincts : une expérience, réalisée à l'Université d’Augsburg, est optimisée pour appliquer les plus forts champs électromagnétiques possibles sur des liquides macroscopiques (78 MV/m) ; l’autre expérience (SPEC/SPHYNX à Saclay) est optimisée pour atteindre la meilleure sensibilité possible pour mesurer un signal 10⁹ fois plus faible que le voltage appliqué. C’est ainsi que nous avons, pour la première fois au monde, pu obtenir la mesure en fonction de la fréquence de χ₅, pour un liquide vitrifiable archétypique : le glycérol (figure ci-contre). À une température donnée, χ₅ présente un pic pour une fréquence définie par le temps de relaxation τ_a : f_a= α/(2πτ_a). Ce pic n’existe pas dans un système trivial de dipôles sans interactions, et c'est donc à cette fréquence que l'on peut tirer une information sur l’ordre amorphe. Pour cette valeur, les résultats des deux expériences indépendantes sont remarquablement proches. On constate, sur la figure 2-B, que le pic est beaucoup plus ample sur χ₅ que sur χ₃, et que χ₁ ne comporte aucun pic : tout ceci est cohérent avec le scénario de l’ordre amorphe qui prévoit non seulement que χ₁ est insensible à l’ordre amorphe, mais aussi que plus on augmente l’ordre de la susceptibilité (à partir de χ₃) et plus les comportements sont violents (aussi bien en fréquence qu’en température).

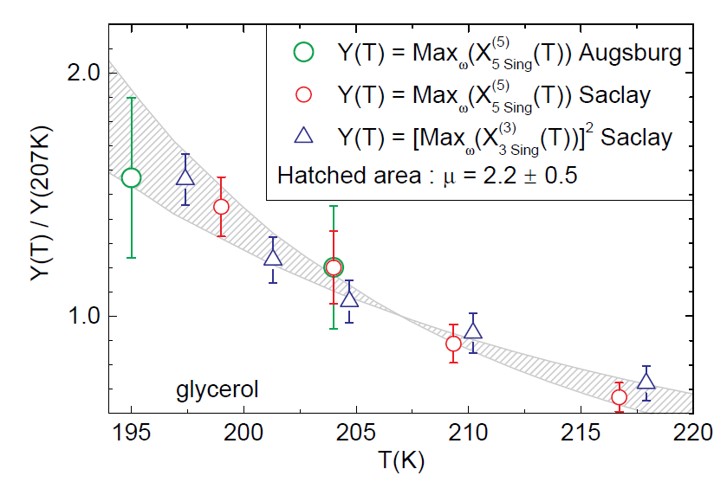
Pour le glycérol. à gauche : comportement de χ₅ en température et en fréquence (ronds : mesures d’Augsburg, carrés : mesures de Saclay), les flèches indiquent f_a. A droite : comparaison des dépendances en fréquence (normalisées pour f5 ,χ₃,χ₁. Les courbes “triviales” correspondent au cas d'un gaz de dipôles sans interactions.

La figure ci-contre complète le panorama en montrant que le maximum de la bosse de χ₅ évolue comme le carré de celle de χ₃, donc bien plus violemment quand on baisse la température. Cette loi d’évolution en température permet de conclure que les domaines d’ordre amorphe, dont la taille augmente avec la baisse de température, sont des domaines compacts : leur dimensionnalité fractale est égale à la dimension 3 de l’espace.

Ces résultats établissent donc l’existence d'un ordre amorphe dans les verres, et que la transition associée représente une toute nouvelle classe d’universalité dans les phénomènes critiques. Des mesures similaires sur un autre liquide archétypique vitrifiable – le propylène carbonate- tendent à montrer la généralité du résultat.

L’existence d'un ordre amorphe invalide un certain nombre d’approches théoriques. Trois théories restent cependant compatibles avec nos expériences (RFOT, Frustration, Plaquettes) : elles diffèrent sur l’ingrédient physique essentiel qui fait que l’ordre amorphe s’institue. Ceci a certaines conséquences observables, que l'on doit pouvoir tester par des expériences d’un tout nouveau type, qui sont l'objet de notre programme de recherche actuel.

C : évolution en température du maximum en fréquence des susceptibilités non linéaires adimensionnées χk. la zone hachurée correspond à χ5 ~ [χ3]µ avec µ = 2.2 ± 0.5.

Références :

[1] S. Albert, Th. Bauer, M. Michl, G. Biroli, J.-P. Bouchaud, A. Loidl, P. Lunkenheimer, R. Tourbot,
C. Wiertel-Gasquet, F. Ladieu, Sciences Juin 2016.

[2] “Evidence of growing spatial correlations at the glass transition from nonlinear response experiments”,
C. Crauste-Thibierge, C. Brun, F. Ladieu, D. L'Hôte, G. Biroli, J.-P. Bouchaud, Phys. Rev. Lett. 104, 165703 (2010).

[3] “Cooperativity and the freezing of molecular motion at the glass transition”,
Th. Bauer, P. Lunkenheimer, A. Loidl, Phys. Rev. Lett. 111, 225702 (2013),
and the associatedf Physics view point :
“Clearing up the mysteries of glassy dynamics”, G. Biroli and J.-P. Bouchaud, Physics 6, November 25, 2013, 128.

Le communiqué de presse CEA-CNRS-ENS-CFM : Transition vitreuse : l'existence d’un ordre dans les verres enfin démontrée !
Le communiqué de l'Université d'Augsburg : “ Glasbildung durch amorphe Ordnung“.

Contacts CEA : François Ladieu (SPEC/SPHYNX) et Giulio Biroli (IPhT).

Collaboration :

S. Albert, R. Tourbot, C. Wiertel-Gasquet, F. Ladieu, groupe SPHYNX au SPEC, CEA, CNRS, Université Paris-Saclay, CEA Saclay Bat 772, 91191 Gif-sur-Yvette Cedex, France.
Th. Bauer, M. Michel, P. Lunkenheimer, A. Loidl, Experimental Physics V, Center for Electronic Correlations and Magnetism, University of Augsburg, 86159 Augsburg, Germany.
G. Biroli, IPhT, CEA, CNRS, Université Paris-Saclay, CEA Saclay Bat 774, 91191 Gif-sur-Yvette Cedex, France, & LPS, École Normale Supérieure, 24 rue Lhomond, 75231 Paris Cedex 05, France.
J.-P. Bouchaud, Capital Fund Management, 23 rue de l’Université, 75007 Paris, France.