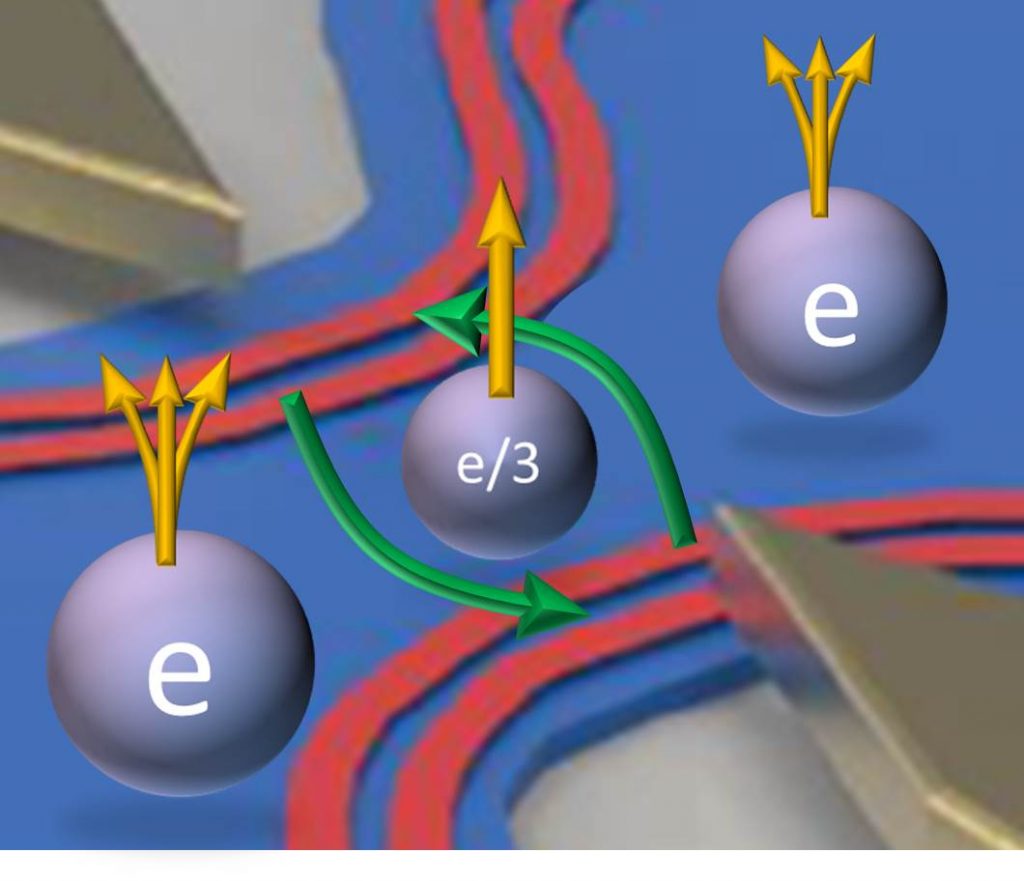
The electron is an elementary particle carrying the elementary charge “e” that is a fundamental constant of physics. However, in a 2-dimensional confined conductor within an intense magnetic field (~ 10 T), the electrons can be organized into a new topologically correlated quantum state so that the electric current can be transported by fractional charges: e / 3, e / 4, e / 5 …. Neither fermions (like electrons) nor bosons (like photons), these artificial elementary particles are called anyons and are thought to obey a “fractional quantum statistic”. Some varieties of anyons could be used for “topological quantum computation”, where the quantum information is carried by well defined states (qubit) that are topologically protected.
A team from the CEA SPEC , in collaboration with the Cavendish Laboratory of Cambridge (UK) for the elaboration of the material, has shown that it is possible to observe and manipulate anyons of fractional charge e * = e / 3 or e / 5, with microwave photons of frequency f. This is evidenced by the observation, in the presence of a V polarization and a microwave field of frequency f, of an excess photo-assisted noise, measured beyond a threshold voltage VJ given by the Josephson relation: e*VJ=hf. These results have just been published in the journal “Science”.
The measurement of this threshold brings a new original determination of the fractional charge of anyons. It also proves that anyons can absorb or emit photons, which opens a way for their time-resolved manipulation and attempts to highlight their fractional statistics.
In a two-dimensional world, the set of elementary particles would be much richer because, in addition to the fermions or bosons of our usual three-dimensional world, there would be the possibility of objects obeying an infinity of intermediate quantum statistics (or anyonic statistics according to the term from the compound word “Any-ons”) [1]. The existence of bosons and fermions results from the symmetry properties of an assembly of these particles: during the exchange of two particles, the total wave function sees its phase unchanged (phase shift = 0) if the particles are bosons, or assigned a phase factor eiπ = -1 for fermions, in agreement with 3-dimensional observations. However, in two dimensions and for the same exchange operation, the phase factor eiθ may take any value, where θ is the “statistical angle”, whose value defines a particular anyonic statistical distribution.
For about thirty years, condensed matter physicists have been studying two-dimensional electronic systems by confining electrons in a plane at the interface of two semiconductors. Very soon new unexpected electronic quantum phases were observed at low temperature in the presence of an external magnetic field. First of all, it was the integer Quantum Hall effect [2], where the evolution of Hall’s resistance, as a function of the intense applied field at low temperature, no longer evolves linearly, but presents quantized plateaux, so precise that they gave rise to a new standard of the electric resistance: the Klitzing.
For stronger field more astonishing phases appear where the Hall conductance becomes a fraction of the unit of conductance (inverse of resistance) [3]. In this regime called “fractional quantum Hall effect”, the current can be carried by quasi particles carrying a fractional charge e * = e/m, m = 3 or 5 … , function of the experimental conditions. Like quarks, the fractional charges e/m cannot be separated in vacuum and must remain confined in the two-dimensional electronic fluid. But unlike quarks, which are fermions, these objects are anyons, presenting the statistical angle π/m. Finding a way to manipulate these anyons to try to highlight their fractional statistics is an experimental challenge, and a first step in that way has just been successfully completed by SPEC researchers. Beyond this advance, it should also be noted that anyons are not only a theoretical curiosity, but also brings a new potential path for quantum computing, based on their manipulation.
Experimental setup and principle of measurement:
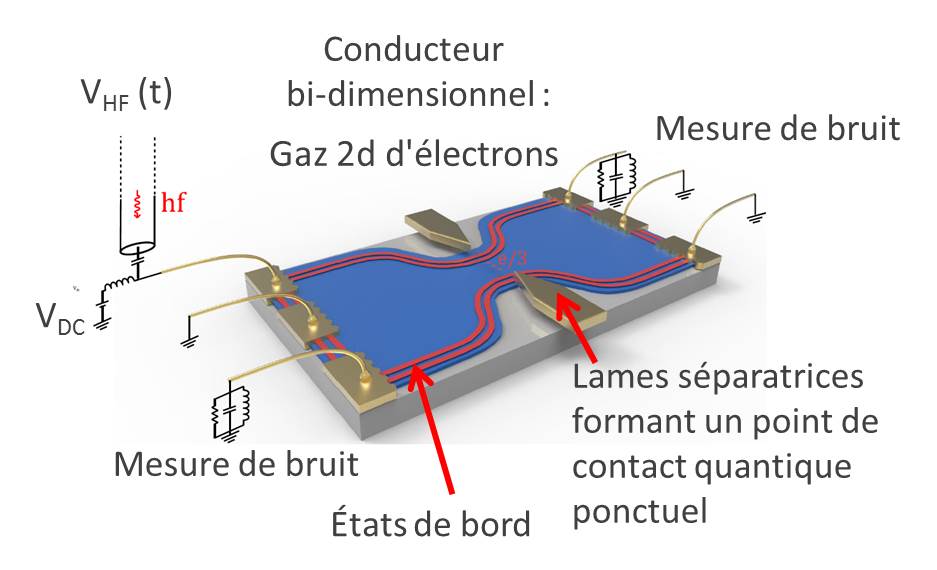
In its principle, the carried out experiment consists of analyzing the electrical noise of a very weak electric current. This current must be low enough for the charges individually pass through the conductor, so generating a shot noise which amplitude is characteristic of the charge of an elementary transport event.
For this, a AsGa/As(Al)Ga semiconductor heterojunction with high electronic mobility was carried out at Cavendish Laboratory in Cambridge (UK) by epitaxial growth. The two-dimensional electron layer is located at the interface, buried by 100 nanometers. With the nanofabrication facilities of SPEC, a conductor a few tens of microns wide is obtained by etching. Electric contacts are added to apply the bias voltage and inject and measure the current, as well as a pair of electrostatic grids whose polarization allows adjusting the width of a conductive constriction in the center of the sample, thus forming a Quantum Point Contact (QPC).
To overcome the thermal noise, the sample is cooled to 20 mK in a dilution refrigerator and subjected to a strong perpendicular magnetic field of about 11 T. The applied strong magnetic field imposes that the current is propagated only in channels along the edges of the sample, with a direction imposed by the sign of the field. The conductor’s core, which is not traversed by any net macroscopic current, forms a Hall topological insulator. A bias voltage V injects an incident current that splits at the level of QCP into a non-deflected (transmitted) current and a “reflected” current between the channels facing each other. In the case of a very weak reflection of the current, the reflected current results from the rare and uncorrelated transfer of charges e*. Since the statistic is Poissonian, the ratio of the shot noise to the average current gives a direct measurement of the charge of the exchanged quasi-particles .
The first measures have consisted in reproducing the results obtained by the same team twenty years ago [4], when the fractional loads (e/3) were observed for the very first time. The new device then allows extending the observation to even smaller fractions of charges: e/5 [5].
Manipulation of fractional electric charges:
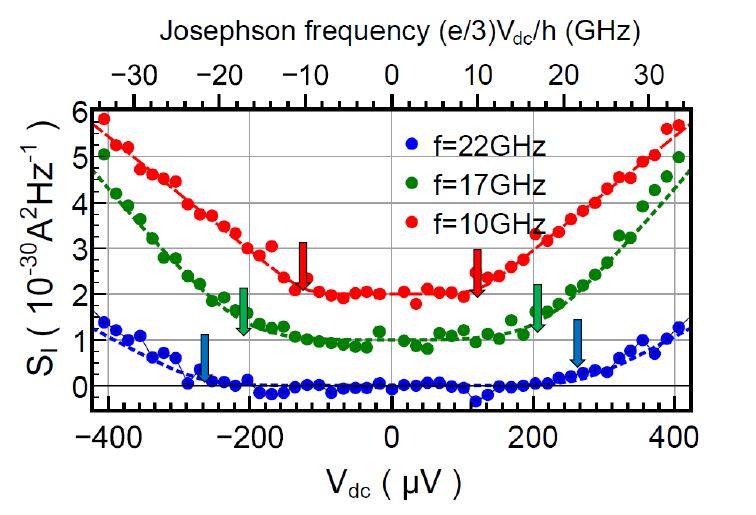
But it is the proof of the emission and absorption of photons by the anyons that is the fundamental discovery of the present study. This interaction provides a second measurement method confirming the reality of the fractional excitations. It also opens the way to controlled time resolved manipulation of anyon . For this, a periodic voltage of microwave frequency f (a few tens of GHz) is superimposed to the DC bias voltage V injecting some current in the conductor. At the working temperature (20 mK), the quantum of energy hf is much higher than the thermal energy. An additional electrical noise, called photo-assisted, is observed, attesting that the quasi-particles are sensitive to photons. This photo-assisted noise appears when the applied bias voltage is beyond a threshold VJ such that e*VJ = ± hf [5]. Checking this fractional Josephson relationship attests that accelerated e* charge in a bias potential V can effectively absorb or emit hf quanta .
Perspectives :
These photo-assisted noise measurements satisfying the Josephson relation thus give a new measure of the fractional charges in agreement with those based on the shot noise of the direct current. This new experience confirms the reality of fractional charge excitations. Their manipulation by microwaves allows considering the possibility to produce on demand time resolved anyon sources (analogous to photon sources) based on levitons (current pulse of Lorentzian form) [6]. With such sources, it becomes possible by two anyons interferometry to point out and explore anyonic statistics.
References:
[1] “On the theory of identical particles”,
J.M.Leinaas, and J.Myrheim, Nuovo Cimento B37, 1-23 (1977).
Quantum mechanics of fractional-spin particles
F.Wilczek, Phys.Rev.Lett. 49, 957 (1982).
[2] “New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance”
K. v. Klitzing, , Physical Review Letters 45(6) (1980) 494.
[3]” Nobel Lecture: The fractional quantum Hall effect”
H. L. Störmer, Reviews of Modern Physics, vol. 71 (1999) 875
[4] “Observation of the e/3 fractionally charged Laughlin quasiparticle”
L. Saminadayar, D.C Glattli, Y. jin et B. étienne, Phys. Rev. Lett. 79, (1997) 2526.
[5] “A Josephson relation for fractionnally charged anyons”
M. Kapfer, P. Roulleau, M. Santin, I. Farrer, D. A. Ritchie and D. C. Glattli, SCIENCE journal, January 24th 2019, see also Arxiv 1806.03117 (Juin 2018).
[6] “Minimal-excitation states for electron quantum optics using levitons”
J. Dubois, T. Jullien, F. Portier, P. Roche, A. Cavanna, Y. Jin, W. Wegscheider, P. Roulleau and D. C. Glattli, Nature 502 (2013) 659.
- Learn more about the first observation of fractional electric charges:
“Le bruit des charges fractionnaires”, Laurent Saminadayar, Pour la science n°289 (2001) 30. - See also the IRAMIS highlight: “Les lévitons : des électrons sans bruit pour l’optique quantique électronique / Levitons: electrons without shot noise for electronic quantum optics” , October 2013.
CEA-IRAMIS contacts: Christian Glattli, et Preden Roulleau, Groupe nanoélectronique SPEC/GNE UMR 3680 CEA-CNRS.
Collaboration ;
- Groupe nanoélectronique SPEC/GNE UMR 3680 CEA-CNRS, CEA Saclay France
And for the supply of the samples:
- Department of Electronic and Electrical Engineering, University of Sheffield, Mappin Street, S13JD, UK
- Cavendish Laboratory, University of Cambridge, J.J. Thomson Avenue, Cambridge CB3 0HE,10 UK




