Magnetism is a field of major interest, because combined with electronics, it has profoundly changed our daily lives: in the form of sensors, actuators, nomadic devices (telephones, tablets, laptops), materials with increased storage capacities for magnetic recording of all our computer data, etc…. Ultimately, quantum computation and quantum computers may yet revolutionize our societies.
On a more fundamental level, magnetism is an ideal terrain for revisiting and even going beyond the paradigms of condensed matter physics, Landau’s theory of phase transitions and Fermi’s theory of liquids. The theory of phase transitions is, however, a formidably effective concept, with a very general scope in physics, creating bridges with field theory, cosmology, etc… With the notion of spontaneous symmetry breaking, phase transition theory has proved a powerful tool for sorting, classifying and understanding complex patterns. In the same way, Fermi liquid theory is an effective way of addressing the role of fermion interactions. This model allows the properties of metals to be described almost like those of a gas of interacting electrons, but where the real electrons are replaced by quasiparticles (electrons dressed up by correlations). However, today’s physics attempts to go beyond these concepts.
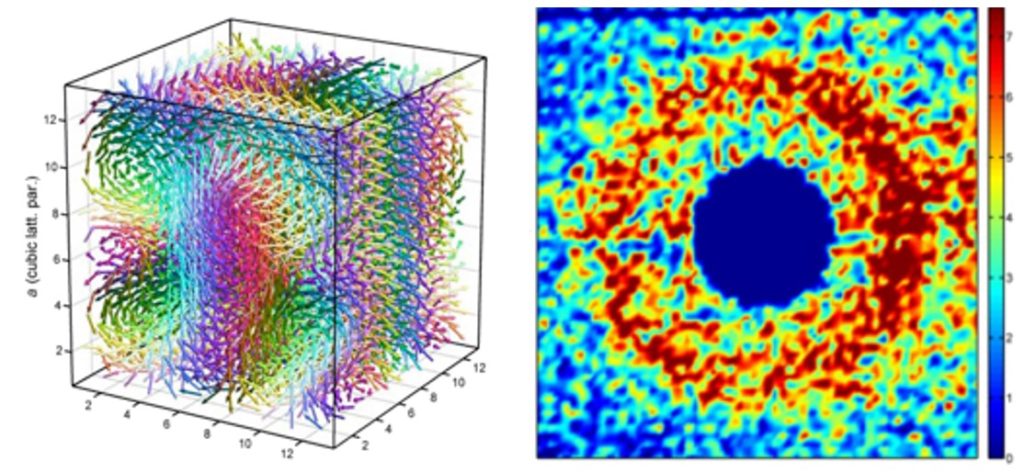
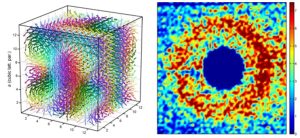
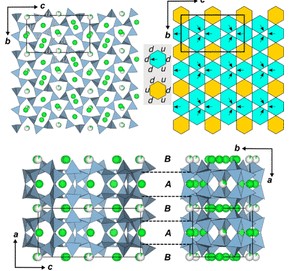
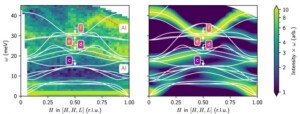
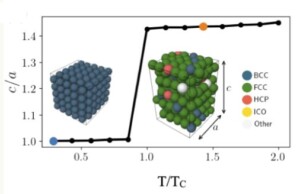
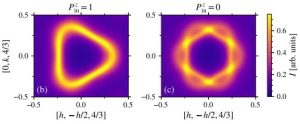
Left: Topology of the triple-twist arrangement in a 12x12x12 unit-cell cluster containing ~7000 spins. Right: SANS color map for Mn0.85Fe0.15Si measured at 1.5 K. The scattering intensity ring is characteristic for partial order. See “Observation of a magnetic “blue phase” in an itinerant magnet“.
New questions have thus arisen, and with them the notions of confinement, of excitations characterized by fractional quantum numbers, and of topological phase transitions. Similarly, in certain materials, anomalies are being observed that call into question our understanding of Fermi liquids, notably the new superconductors or so-called “Kondo” systems. These observations highlight the role of coulombic interactions between electrons, known under the general term of “correlations”, which open the way to new concepts.
Neutron scattering plays a central role in understanding magnetic properties. Sensitive to volume (and not just surfaces), magnetic moments and their static and dynamic correlations, neutron scattering is a leading experimental probe for studying magnetism, and consequently for exploring this new physics. For example, it can be used to determine complex magnetic structures with unrivalled precision, to characterize and model magnetic interactions using inelastic neutron scattering, or to probe the magnetic properties of molecular and nanometric systems. These unique investigative capabilities are a major advantage of neutron scattering (magnetic information is of the same order of magnitude as structural information for neutrons, whereas it is at least 10,000 times weaker for X-rays).