
We thought we knew transistor physics fairly well and in particular the millions of MOSFETs (Metal Oxyde Semi-conducteur Field Effect Transistor) which can be found at the core of our computers. However, as early as 1994, a new generation of very high mobility MOSFETs lead to experiments where one could study the regime of extremely low density (Kravchenko et al 1994). The experiments performed on these “extreme transistors” showed very spectacular behaviors: at low density, instead of the expected insulator, one observes a good metallic behavior. (Instead of a divergence of the resistivity at low temperature, one finds that the resistivity decreases by an order of magnitude in a rather narrow window of temperature).
No metal in 2 dimensions. In order to understand why these experimental results were at the origin of a very important research activity, both theoretical and experimental, one must go back to the celebrated article of P.W. Anderson (« Absence of diffusion in certain random lattices », Anderson 1958) for which he was later given the Nobel prize. Anderson studies the effect of a very weak disorder in metals and concludes that at very low temperature (i.e. for a system with quantum coherence), the multiple interferences generated by the reflections on this disorder lead to the localization of the metal wave functions, hence to an insulating behavior. In particular, the effect is very strong in one and two dimensions (as in our MOSFETs) where one finds that an arbitrary weak disorder is enough to drive the system to the insulating limit. During the next 20 years, the scientific community studied localization and verified this paradigm both experimentally and theoretically: there is no metal in two dimensions. The SPEC laboratory was at the origin of key contributions, through in particular, the work of M. Sanquer and J-L Pichard.
The ideal suspect, electronic correlations. The Kravchenko experiments, later reproduced in various experimental groups (including at SPEC in D. L’hôte group) were at the origin of a small revolution in the quantum transport community. Models and physical mechanisms to explain the experimental data came from everywhere to try and conciliate the theory with the observed metallic behavior. Some were looking for experimental artifacts why others came up with weird or ad hoc models. There was only one point on which everybody agreed on : at very low density, electron-electron correlations due to Coulomb repulsion are huge and should be seriously taken into account in the theory. The bad news was that these correlations resist to most theoretical approaches.
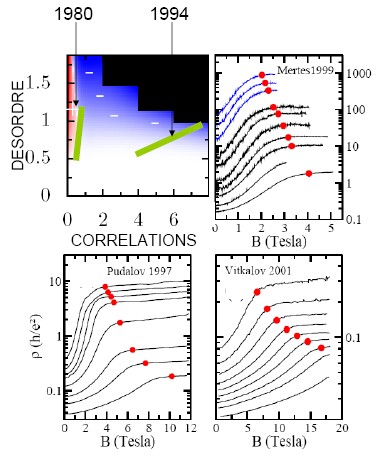
Localization and Corelations. During the PhD thesis of Geneviève Fleury, we have developed a numerical approach which uses quantum Monte-Carlo to solve the quantum many-body problem and scaling theory to extract the thermodynamic limit. With this approach, we were able to study, for the first time, the problem of the interplay between Anderson localization and electron-electron correlations. The phase diagram that we have obtained ab-initio (without any adjustable parameters) does show a metallic phase in the experimental regime where it was observed (see figure). The scenario that emerges from our calculations is mixed: On one hand correlations are at the origin of the experimental observations so that new physics arises from the correlations. On the other hand the system is still an insulator in the thermodynamical sense. In other words, we predict that at even lower temperatures the resistivity must diverge in accordance with Anderson localization paradigm.
References:
[1] P. W. Anderson, Phys. Rev. 109, 1492 (1958)
[2] S. V. Kravchenko, G. V. Kravchenko, J. E. Furneaux, V. M. Pudalov, and M. D’Iorio, Phys. Rev. B 50, 8039 (1994
[3] J.-L. Pichard and G. Sarma, J. Phys. C 14, L127 (1981)
[4] Jean-Louis Pichard, Marc Sanquer, Keith Slevin, and Philippe Debray Phys. Rev. Lett. 65, 1812 (1990)
[5] R. Leturcq, D. L’Hôte, R. Tourbot, C. J. Mellor, and M. Henini, Phys. Rev. Lett. 90, 076402 (2003), http://fr.arxiv.org/abs/0902.3171
[6] G. Fleury and Xavier Waintal, http://fr.arxiv.org/find/cond-mat/1/au:+Fleury_G/0/1/0/all/0/1
[7] G. Fleury and X. Waintal, Phys. Rev. Lett. 101, 226803 (2008)
[8] G. Fleury and X. Waintal, Phys. Rev. Lett. 100, 076602 (2008)
Contacts : Geneviève Fleury et Xavier Waintal



