Fundamental interest of plasma mirrors
One of the main motivations for investigating plasma mirrors is purely fundamental. What better model system can be found than one where the field laser impinges a plasma with an almost step-like interface with the vacuum? Plasma mirrors are ideal ‘toy’ models to decipher the elementary processes involved in UHI physics, in particular by confronting experimental findings with predictions of models and numerical simulations.
Generation of high-order harmonics and attosecond pulses
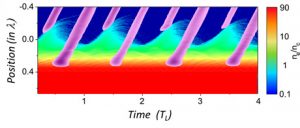
At very high laser intensities (I>1016 W/cm2), the response of plasma mirrors to the laser field becomes highly non-linear, leading to the generation of high-order harmonics of the incident laser frequency in the reflected beam [Teu09,Tha10], associated in the time domain to trains of intense attosecond pulses (Fig.1). The main mechanisms leading to this emission -Coherent Wake Emission (CWE) [Que06,Tha10] and the Relativistic Oscillating Mirror (ROM) process [Lic91,Bae06,Dro06,Tha07,Gon11] – are now well-identified and qualitatively understood. In CWE, the emission results from collective electron oscillations in the dense plasma, triggered by attosecond bunches of fast electrons injected by the laser field from the plasma surface into its bulk. The ROM process comes into play at much higher intensities (I>1018 W/cm2): the attosecond pulse emission then occurs through the periodic Doppler effect induced on the reflected field by the laser-driven relativistic oscillation of the mirror surface.
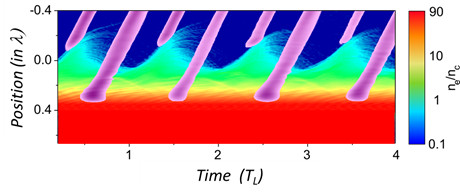
Fig. 1: Generation of attosecond pulses from plasma mirrors by CWE and ROM. This image shows results from Particle-In-Cell simulations (from [Que06]). The color map shows the electronic density in log scale, and the purple map the intensity of the generated attosecond pulses . The calculation was performed with an angle of incidence of 45 deg, a density gradient of λ/15, and a constant intensity of 4.1017 W/cm2. The incident laser field propagates from negative to positive x. The attosecond pulses originating from near the critical density surface are due to ROM, and the ones coming from the much denser part of the plasma are produced by CWE.
Vacuum laser acceleration of relativistic electrons
Correlated with this light emission and close to the direction of specular reflection, beams of relativistic electrons (≈ 10 MeV energies for I=3.1019 W/cm2, see Fig. 1) are also produced towards the vacuum. Electrons are ejected out of the plasma surface in the form of attosecond bunches, with a relativistic velocity along the direction of the specularly reflected laser field (Fig.2a). These electrons thus co-propagate with the reflected laser beam in vacuum, and can interact with it over distances on the order of the Rayleigh length (Fig.2b). By acting as injectors of electrons in the laser field, with measured charges in the 10 nC range, plasma mirrors thus open the way for the first time to the investigation of the dynamics of free relativistic electrons in ultraintense laser fields. This is a subject of high fundamental interest that has motivated considerable theoretical work in the last decades, but which had so far remained inaccessible experimentally.
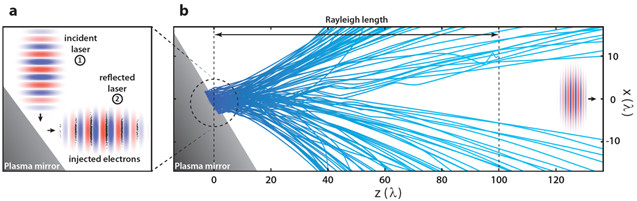
Fig. 2: Injection of relativistic electrons in ultraintense laser fields using plasma mirrors. Panel a): principle of a plasma mirror injector. As an ultraintense laser pulse (E-field sketched in red and blue) reflects on a plasma mirror, it expels relativistic electrons (black dots) at specific phases of the field. These electrons then interact with the reflected pulse in vacuum. Panel b) shows electron trajectories (blue lines) computed from a 2D PIC simulation of the laser-plasma interaction. Electrons were initially located in the vicinity of the surface of the plasma mirror. Once expelled from the surface, they co-propagate and interact with the reflected laser field over a distance of the order of the Rayleigh length. This interaction clearly modifies the electron angular distribution as electrons are expelled to the side of the focal volume.
[Bae06] Baeva et al, Phys. Rev. E 74, 046404 (2006)
[Bra09] Brandl et al, Phys. Rev. Lett. 102, 195001 (2009)
[Dro06] Dromey et al, Nature Physics 2, 456 – 459 (2006)
[Gei06] Geindre et al, Phys. Rev. Lett. 97, 085001 (2006)
[Gei10] Geindre et al, Phys. Rev. Lett. 104, 135001 (2010)
[Gon11] Gonoskov et el, Phys. Rev. E 84, 046403 (2011)
[Lic91] Lichters et al, Phys. Plasmas 3, 3425 (1996)
[Mor09] Mordovanakis et al, PRL 103, 235001 (2009)
[Teu09] Teubner & Gibbon, Rev. Mod. Phys. 81, 445 (2009)
[Tha07] Thaury et al, Nature Physics 3, 424 – 429 (2007)
[Tha10] Thaury & Quéré, J. Phys. B. 43, 213001(2010)
[The15] Thévenet et al, submitted to Nature Physics