Effets collectifs dans la réponse dynamique des atomes du plasma

Certaines applications qui impliquent des plasmas denses (fusion inertielle, naines blanches, par exemple) révèlent l’importance de l’interaction des configurations et des effets collectifs dans la modélisation des propriétés optiques du plasma. Les cas les plus difficiles sont ceux où un mélange de canaux apparaît impliquant les transitions électroniques liés-liés, liés-libres et libres-libres. Le traitement des électrons libres dans les plasmas partiellement ionisés est très souvent différent de celui des électrons liés. Ceci est lié au fait que le la densité électronique correspondant au spectre continu d’électrons n’est pas localisée et ne peut pas être considérée comme « atomique ». Cependant, afin de tenir compte du mélange de canaux et d’éviter des incohérences dans le calcul des spectres d’absorption, tous les électrons devraient, en principe, être décrits dans un même formalisme.

Afin d’améliorer les modèles actuels des propriétés radiatives des plasmas, nous avons développé deux modèles variationnels d’atome-moyen à l’équilibre : un modèle quasi-classique de Thomas-Fermi [Felderhof 1995abc, Ishikawa 1998, Blenski 2013] et un modèle quantique [Blenski 2007, Piron 2011, Piron 2013]. Nous avons également développé le formalisme de la réponse linéaire dynamique pour chacun de ces modèles [Blenski 1992, Blenski 2006, Caizergues 2013, 2015, 2016, Piron 2018]. Il s’agit ici d’un formalisme auto-cohérent dans lequel une densité induite, dépendante de la fréquence, contribue au champ électrique perturbateur représentant les photons du rayonnement. Dans ces modèles, les électrons liés et libres sont traités dans le même formalisme. Nous avons d’abord développé une approche numérique de la photo-absorption dans les plasmas, fondée sur le modèle de Thomas-Fermi. Cette approche permet l’inclusion de certains effets collectifs dans le calcul des propriétés radiatives des plasmas. Dans le cas de la réponse linéaire Thomas-Fermi, nous avons réussi à prouver une règle de somme [Caizergues 2013, 2015, 2016,] analogue à celle que nous avions proposée dans [Blenski 2006] dans le cadre de la théorie quantique. La relative simplicité du modèle Thomas-Fermi nous a permis de vérifier cette règle de somme par des calculs numériques directs. Elle peut être considérée comme une généralisation de la relation entre les formes de longueur et d’accélération de la matrice dipolaire (règle de somme de « Ehrenfest » pour les atomes dans les plasmas). Elle fournit à la fois un moyen de calculer le dipôle induit s’appuyant uniquement sur des intégrales absolument convergentes et un schéma d’interprétation permettant de distinguer dans la photo-absorption une contribution de freinage (inverse Bremsstrahlung) et une contribution collective.

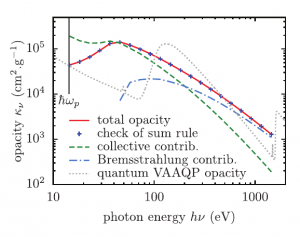
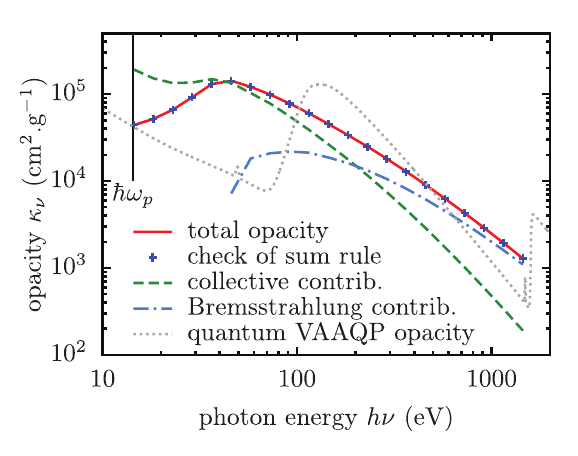
La Fig. 1 présente l’opacité d’un plasma d’aluminium à la température de 10 eV et la densité du solide. L’opacité, calculée dans le modèle de la réponse linéaire du Thomas-Fermi, a été obtenue par le calcul direct et à l’aide de la nouvelle règle de somme. La comparaison démontre la précision du calcul fondé sur la règle de somme. Cette dernière donne l’accès à la contribution collective l’absorption qui semble dominer la photo-absorption pour les photons de basse énergie. Cependant, dans le cas étudié à la figure 1, cette région s'étend de la fréquence plasma jusqu’à 200 eV, ce qui ne semble pas physique.

Le modèle Thomas-Fermi de la réponse linéaire constitue un bon banc d’essais théoriques. Ce modèle permet, entre autres, de forcer la densité induite dépendante de la fréquence à avoir un comportement du type « ondes sortantes » loin de l’atome. Les études sur ce modèle nous ont permis de comprendre l’importance de la forme asymptotique de la densité induite. Il est nécessaire que cette densité soit exactement donnée par l’expression des ondes sortantes afin de pouvoir remplir la nouvelle règle de somme. Cette observation est importante pour l’extension de la réponse dynamique linéaire à des cas purement quantiques. Cette extension constitue l’objectif final dans notre recherche. En effet, le modèle Thomas-Fermi, bien qu’utile pour l’équation d’état, peut néanmoins conduire à de médiocres estimations des propriétés radiatives. Ceci est notamment dû à l’absence de la structure en couches, qui est nécessaire pour tenir compte des modes électrons-trous, ainsi qu’à la singularité de la densité d’électrons Thomas-Fermi près du noyau, qui conduit à un comportement incorrect de la section efficace à haute fréquence. Pour illustrer ces points, le résultat de la réponse linéaire en formalisme des électrons indépendants du modèle VAAQP quantique est également montré dans la Fig. 1.

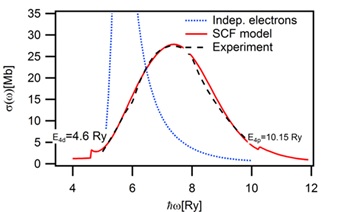
Fig. 1: Opacité d’un plasma d’Al à une température de 10 eV et densité du solide, calculée à l’aide de la réponse linéaire dynamique auto-cohérente du modèle de Thomas-Fermi. Le résultat de la réponse linéaire en particules indépendantes du modèle VAAQP quantique est également montré, à titre de comparaison.

Une étude préliminaire de la réponse linéaire dynamique auto-cohérente partant du modèle quantique VAAQP (« Variational Average Atom in Quantum Plasma » ) a aussi été réalisée [Caizergues 2016]. Dans les calculs fondés sur notre formalisme, la règle de somme n’a pas été vérifiée en raison de problèmes mathématiques avec l’inclusion de la condition limite des ondes sortantes. Cependant, dans le cadre de ces recherches, nous avons développé un code du calcul de la photo-absorption quantique permettant de tenir compte de certains effets collectifs comme le mélange des canaux entre les transitions liés-liés et liés-libre. Nous avons entre autres vérifié l’effet de ce mélange des canaux entre les transitions liés-liés et liés-libre dans le cas de l’atome du Xénon à température nulle (fig. 2), en reproduisant les résultats de [Zangwill 1980].

Références :

[Piron 2018] Piron R and Blenski T, “Average atom model calculations of dense plasma opacities: Review and potential applications to white dwarf stars“, Contributions to Plasma Physics. Vol. 58(1), pp. 30-41, (2018).
[Caizergues 2016], Caizergues C, Blenski T and Piron R, “Dynamic linear response of atoms in plasmas and photo-absorption cross-section in the dipole approximation “, High Energy Density Physics. Vol. 18, pp. 7 – 13, (2016),
[Caizergues 2015], Caizergues C , “Réponse linéaire dynamique et auto-cohérente des atomes dans les plasmas quantiques : photo-absorption et effets collectifs dans les plasmas denses“., Thesis at: Université Paris XI – Paris Sud., (2015).
[Caizergues 2015], Caizergues C, Blenski T and Piron R, “Linear response of a variational average atom in plasma: Semi-classical model “, High Energy Density Physics. Vol. 12(0), pp. 12 – 20 – (2014).
[Blenski 2013], Blenski T, Piron R, Caizergues C and Cichocki B,”Models of atoms in plasmas based on common formalism for bound and free electrons “, High Energy Density Physics. Vol. 9(4), pp. 687 – 695 – (2013).
[Piron 2013], Piron R and Blenski T,”Variational Average-Atom in Quantum Plasmas (VAAQP) – Application to radiative properties“, High Energy Density Physics. Vol. 9(4), pp. 702 – 710 – (2013).
[Felderhof 1995a], B. U. Felderhof, T. Blenski, and B. Cichocki, “Dielectric function of an electron-ion plasma in the optical and X-rays regime“, Physica A, 217, 161 (1995).
[Felderhof 1995b], B. U. Felderhof, T. Blenski, and B. Cichocki, “Collective contribution to the frequency-dependent polarizability of an ion or metallic cluster immersed in a plasma “, Physica A, 217, 175 (1995).
[Felderhof 1995c], B. U. Felderhof, T. Blenski, and B. Cichocki, “Frequency_dependent extinction cross-section of sperical ion or metallic cluster immersed in a plasma“, Physica A, 217, 196 (1995).
[Blenski 2007] T. Blenski, B. Cichocki, “Variational theory of average-atom and superconfigurations in quantum plasmas“, Phys. Rev. E 75 (2007) 056402.
[Piron 2011] R. Piron, T. Blenski, “Variational-average-atom-in-quantum-plasmas (VAAQP) code and virial theorem: equation-of-state and shock-Hugoniot calculations for warm dense Al, Fe, Cu, and Pb“, Phys. Rev. E 83 (2011) 026403.
[Blenski 2006] T. Blenski, “On the linear dynamic response of average atom in plasma“, J. Quant. Spectrosc. Radiat. Transf. 99 (1–3) (2006) 84–101.
[Blenski 1992] T. Blenski, B. Cichocki, “Linear response of partially ionized, dense plasmas“, Laser Part. Beams 10 (2) (1992) 299–309.
[Ishikawa 1998] K. Ishikawa, B.U. Felderhof, T. Blenski, B. Cichocki, “Photoabsorption by an ion immersed in a plasma at any temperature“, J. Plasma Phys. 60 (1998) 787–810, 10.
[Zangwill 1980] A. Zangwill, P. Soven, , “Density-functional approach to local-field effects in finite systems: Photoabsorption in the rare gases“, Phys. Rev. A 21 (1980), 1561.