In chemically ordered compounds with short-range magnetic interactions, geometrical frustration appears when all interactions cannot be satisfied simultaneously due to the lattice geometry. A well-known example is a triangle of antiferromagnetically coupled spins. This frustration results in a strong degeneracy of the ground state, since many configurations have the same energy. It now appears as a powerful ingredient for designing materials or tuning physical properties, since frustrated magnetic states may be easily switched by small changes in the energy balance. Pyrochlores R2Ti2O7 (where R3+ is a rare earth ion) are model systems showing exotic short-range magnetic orders called “spin liquids” and “spin ices”, with unconventional excitations akin to magnetic monopoles, and a huge sensitivity to perturbations. Various aspects have been studied in collaborations with P. Bonville and A. Forget (IRAMIS/SPEC, Saclay), G. Dhalenne and C. Decorse (ICMMO, Orsay), and H. Mutka (ILL, Grenoble).
Local susceptibility in R2Ti2O7 pyrochlores (R = Tb, Ho, Yb, Er)
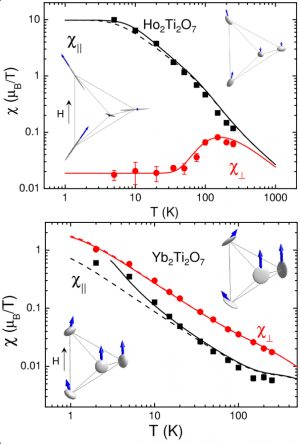
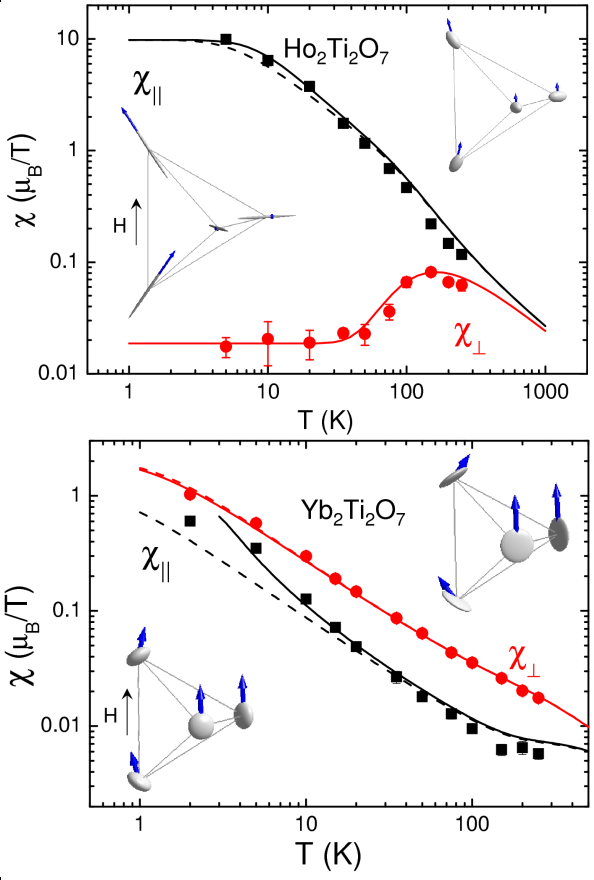
Rare earth titanate pyrochlores of Fd-3m space group, where the R3+ ions occupy the summits of corner-sharing tetrahedra and the Ti4+ ions are nonmagnetic, show very different ground states, such as spin-liquid (Tb) and spin-ice (Ho) states, short range orders, planar antiferromagnetism (Er), and 2D ferromagnetism (Yb). Their physics is governed by the exchange and dipolar interactions between the R3+ ions, together with the crystal-field anisotropy along the <111> axes. The study of the paramagnetic state under applied fields points to precursor effects of these ground states. Single-crystal polarized neutron diffraction gives access to the local susceptibility tensor in the Gukasov-Brown model [1], which reduces to 2 components χ// and χ⊥ with respect to the <111> local axis, owing to the high symmetry the R3+ site. This allows one to describe the complex field-induced structures using only two parameters. This tensor cannot be derived from the bulk magnetization due to the equivalent <111> axes. Measurements performed in four typical cases where the R-R interactions may be F or AF, and the crystal-field anisotropy either Ising- or XY-type, showed that the local susceptibility is highly anisotropic (Figure 1). This is the first determination of the local susceptibility in the Ho2Ti2O7 spin ice with (F, Ising) behavior. Comparison with a calculation of the non-interacting susceptibility deduced from the crystal-field scheme (measured independently by inelastic neutron scattering) yields the tensor of exchange interactions, which is also found to be anisotropic [2]. As a surprising consequence, in Yb2Ti2O7 with (F, XY) behavior, crystal-field and exchange anisotropies nearly compensate, yielding a Curie susceptibility and ground state fluctuations in an original “exchange spin-ice” ground state [3].
[1] Determination of atomic site susceptibility tensors from polarized neutron diffraction data, A. Gukasov and J. Brown, J. Phys. Condens. Matter 14, 8831, (2002).
[2] Ising versus XY Anisotropy in Frustrated R2Ti2O7 Compounds as “Seen” by Polarized Neutrons, H. Cao, A. Gukasov, I. Mirebeau, P. Bonville, C. Decorse, G. Dhalenne, Physical Review Letters 103, 056402 (2009).
[3] Anisotropic exchange in frustrated pyrochlore Yb2Ti2O7
H. Cao, A. Gukasov, I. Mirebeau, P. Bonville, J. Phys. Cond. Mat. Fast Track, 21, 492202 (2009).
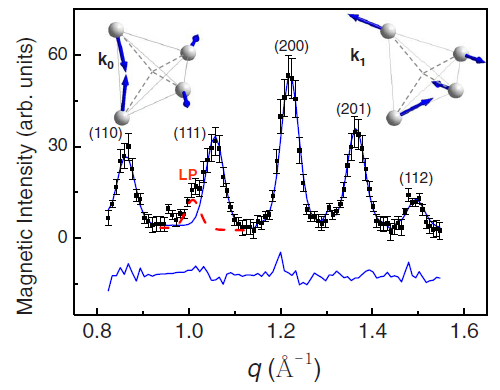
Evolution of the spin liquid Tb2Ti2O7 ground state under applied field
Tb2Ti2O7 realizes the (AF, uniaxial) case with a highly tunable spin-liquid ground state, which is easily destabilized by an applied field, pressure, or magnetic substitution. This tunability results from the peculiar Tb3+ crystal field scheme, with two low-energy doublets easily populated by temperature, or mixed by the magnetic field, and from R-R effective (dipolar + exchange) interactions at the border between the F and AF characters. Starting from the spin-liquid ground state, a magnetic field close to a <110> axis splits the system into two sublattices (α and b chains) and induces spin-ice–like local structures with k = 0 propagation vector, but with different moment values on the two sublattices [1]. Above 2 teslas, magnetic structures with k = 0 and k = (001) propagation vectors coexist. The high sensitivity of the spin structures to a small disorientation of the applied field results from the anisotropic susceptibility. In true spin ices (R = Ho or Dy), this feature was used as a trick to tune the concentration of magnetic monopoles [2].
[1] Field-Induced Spin-Ice-Like Orders in Spin Liquid Tb2Ti2O7
H. Cao, A. Gukasov, I. Mirebeau, P. Bonville, Phys. Rev. Lett. 101, 196402 (2008).
[2] T. Fennell et al. Nature Physics 3, 566 (2007); D. J. P. Morris et al., Science 326, 411, (2009).
An ordered spin ice Tb2Sn2O7 under high pressure
Starting from the Tb2Ti2O7 spin liquid, substitution of Ti by Sn yields a lattice expansion and the onset of an ordered spin-ice state. The change in the energy balance is understood as follows: the lattice expansion favors the dipolar (F) Tb–Tb interactions at the expense of the (AF) superexchange interactions, since superexchange depends more strongly on interatomic distances. The ordered or “soft” spin ice, whose anisotropy is reduced in comparison with the true spin ice, has the local spin ice spin structure (mathematically identical to proton order in water ice) but not its degeneracy, since all tetrahedra of the pyrochlore structure have the same orientations. This leads to long-range order, ferromagnetic magnetization, and intricate spin dynamics [1]. What happens when one pressurizes a soft spin ice? We observed three effects: a reorientation of the spin-ice structure, the onset of antiferromagnetic order, and the enhancement of spin-liquid fluctuations [2]. It is worth noting that only the soft spin ice Tb2Sn2O7 is sensitive to pressure (Figure 2). In the true spin ice Ho2Ti2O2, although theory predicts a pressure tuning of the magnetic monopoles, it was not observed up to now. Very high pressures are likely necessary to disturb the crystal- field scheme and exchange interactions.
I. Mirebeau, H. Mutka, P. Bonville, A. Apetrei A. Forget, Phys. Rev. B 78, 174416, (2008)
[2] Magnetic order in Tb2Sn2O7 under high pressure: From ordered spin ice to spin liquid and antiferromagnetic order
I. Mirebeau, I. Goncharenko, H. Cao, A. Forget, Physical Review B, Rapid Commun. 80, 220407R (2009).