Exploring the properties of the vacuum, now described by quantum electrodynamics (QED), remains one of the objectives of contemporary fundamental physics. In particular, it is predicted that for laser illumination beyond the Schwinger limit (> 4.7×1029 W/cm2), it is possible to separate the virtual electron-hole pairs resulting from vacuum fluctuations.
To reach this threshold, ultra-intense laser physicists, including those at LIDYL, are seeking to spatially and temporally compress laser pulses. To carry out this research, it is also essential to know how to characterize these ultra-short pulses in the femto, or even attosecond range, and focused over distances of the order of nanometers. LIDYL’s PHI team is presenting an original method for spatio-temporal characterization of these ultra-intense laser pulses, based on ptychography* techniques.
From the Greek “ptycho”, to fold, and “graphia”, to write. The technique consists in producing images by scanning the object to be observed, with a strong overlap between each scan.
En 2019 des simulations PIC (particle in cell) à 3 dimensions, réalisées au laboratoire ont montré qu’il était possible d’augmenter l’éclairement obtenu par réflexion sur un miroir plasma, à même de comprimer spatio-temporellement l’impulsion initiale*. Le laser UHI100 de l’équipe PHI du LIDYL produit des impulsions laser femtoseconde de ultra-haute intensité, jusqu’à des éclairements de 5×1019 W/cm2. Il a été utilisé pour vérifier expérimentalement ces prédictions des calculs numériques et un gain d’un facteur 10 en intensité a été observé.
La technique de caractérisation utilisée dans ce travail est une extension des méthodes d’imagerie sans lentilles connues sous le nom de méthodes ptychographiques. Elle consiste à balayer un objet inconnu avec un champ lumineux spatialement cohérent. On observe ensuite “en champ lointain” la manière dont le faisceau est diffracté en fonction de la position de la tache focale sur l’objet. La force de la méthode vient du fait que grâce à un algorithme de “détermination de la phase”, on peut reconstruire à la fois l’objet et le champ lumineux en amplitude et en phase. La dimension temporelle est obtenue en déplaçant l’objet sous le faisceau d’une manière contrôlée. Plus on souhaitera accéder à des résolutions temporelles élevées, plus cette vitesse devra être élevée.
Expérimentalement, l’objet diffractant doit être modulable temporellement à l’échelle attoseconde et spatialement à l’échelle de l’empreinte du laser incident sur le miroir plasma, soit quelques microns. Ceci est obtenu en faisant interférer sur la surface une seconde impulsion de fréquence différente de l’impulsion pompe (figure 1) et qui interfère. La figure d’interférence évolue continûment le long de la surface avec une vitesse donnée par c/(2sin(θ)), où θ est l’angle entre les deux faisceaux.
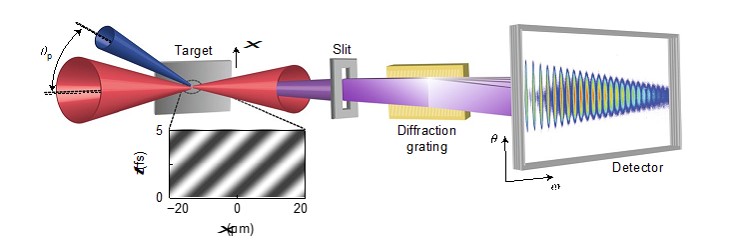
Figure 1 : schéma expérimental – Le laser de pompe (rouge) interfère avec un laser peu intense (bleu), ce qui génère la figure de diffraction dynamique (encart). On observe les distributions angulaires des harmoniques générées sur un écran en champ lointain.
Un laser à impulsions brèves contient une multitude de fréquences réparties sur une largeur donnée par la relation de Fourier temps-fréquence. Une impulsion de 20 fs à 800 nm possède une largeur spectrale de 50 nm. Ces impulsions peuvent, tout en conservant le même spectre, être beaucoup plus longues. On parle d’impulsions “chirpées”** et dans ce cas les différentes fréquences sont étalées dans le temps.
Supposons que la surface modulée précédente se déplace à vitesse constante sous le laser et supposons que toutes les fréquences constitutives de ce dernier soient en phase c’est à dire groupées temporellement. Dans ce cas, pour une position donnée de l’objet sous le faisceau (x0 dans la figure 2), toutes les fréquences vont sonder l’objet au même instant. Ainsi, l’oscillation périodique du faisceau diffracté sera identique pour toutes les fréquences et tout oscillera en phase (figure 2b). En revanche, si toutes les fréquences n’arrivent pas en même temps (faisceau chirpé**), chacune d’elle verra un objet différent et un déphasage entre les différentes composantes spectrales sera observé (figure 2d). La vitesse de déplacement étant connue, ce déphasage contient directement l’information sur la manière dont les fréquences sont réparties dans le temps au sein de l’impulsion. Il donne donc accès à la phase temporelle du champ incident, ce qui combiné à chaque trace ptychographique contient potentiellement toute l’information spatio-temporelle recherchée.
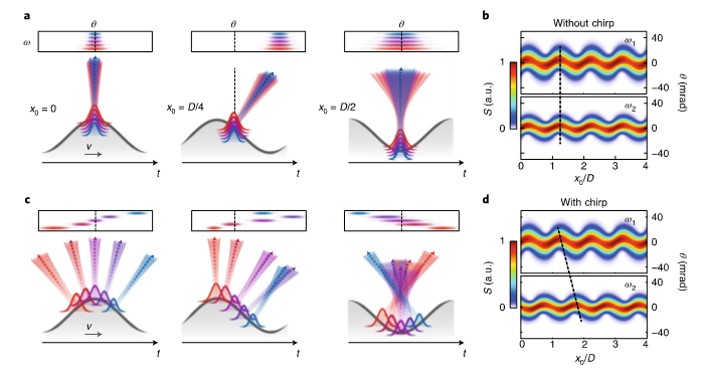
Figure 2 : schéma expérimental – Le laser de pompe (rouge) interfère avec un laser peu intense (bleu), ce qui génère la figure de diffraction dynamique (encart). On observe les distributions angulaires des harmoniques générées sur un écran en champ lointain.
La figure 3 montre pour un champ laser incident supérieur à 1019 W/cm2, la trace ptychographique associée à l’harmonique 9, accompagnée de sa reconstruction avec l’algorithme de “recouvrement de la phase” permettant de reconstruire le champ associé au niveau du miroir plasma.
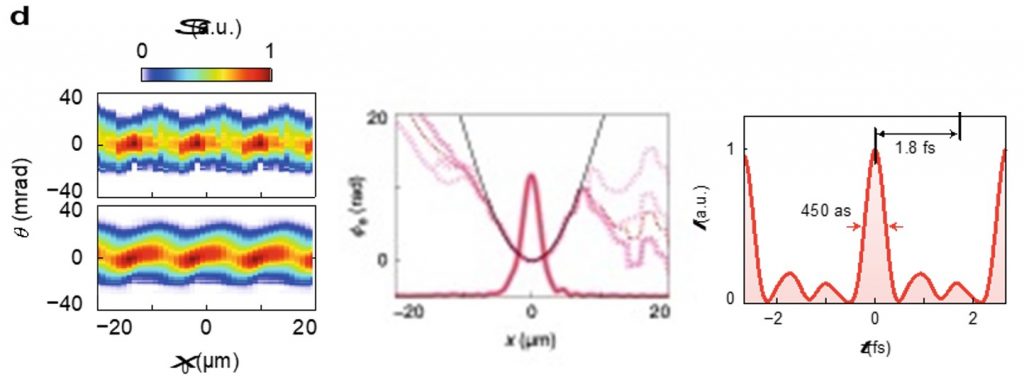
Figure 3 : Gauche : reconstruction du réseau de diffraction vu par l’harmonique 9 (H9). Milieu : Phase et amplitude spatiale de H9. Droite : reconstruction temporelle du champ (harmoniques 9 à 14) moyenné spatialement.
Sur la figure 3, on note que la phase est parabolique, ce qui témoigne de l’action de la pression de radiation provoquée par la distribution d’intensité gaussienne du laser incident. Cet effet renforce la focalisation du faisceau harmonique et la concentration spatiale d’intensité. Avec les données obtenues pour toutes les harmoniques, l’impulsion au niveau du foyer peut être reconstruite par transformée de Fourier. Un profil d’intensité de 450 attosecondes (450 10-18 s) est ainsi mesuré, à comparer à la durée du cycle optique initial de 2.3 fs.
La méthode de caractérisation développée permet ainsi de montrer, conformément aux prédictions théoriques*, l’excellente compression spatio-temporelle observée par la réflexion sur le miroir plasma. Elle permet ainsi de gagner un facteur 10 en éclairement instantané portant les 1019 W/cm2 initiaux à 1020 W/cm2, ce qui ouvre la voie vers des éclairements de 1025 W/cm2 que l’on peut espérer obtenir avec les lasers PetaWatt de dernière génération, et rapproche du seuil du “Champ de Schwinger”.***
References:
[1] “Spatio-temporal characterization of attosecond pulses from plasma mirrors”
L. Chopineau, A. Denoeud, A. Leblanc, E. Porat, P. Martin, H. Vincenti & F. Quéré, Nature Physics., Vol 17, August (2021)
[2] Achieving Extreme Light Intensities using Optically Curved Relativistic Plasma Mirrors”,
H. Vincenti, Phys. Rev. Lett.RL 123, (2019) 105001
*Miroir plasma, et simulation PIC-3d, voir le fait marquant 2019 : “Code de calcul massivement parallèle pour une simulation ab-initio de l’interaction laser-matière à ultra-haute intensité : atteindre une compression de 1025 W.cm-2“.
Voir aussi (2022) : “Miroir plasma : un pas supplémentaire pour approcher la limite de Schwinger et sonder le vide“
Contact CEA-IRAMIS : Philippe Martin et Henri Vincenti, (LIDYL/PHI)
Collaboration :
• Adrien Leblanc, LOA – Laboratoire d’Optique Appliquée, ENSTA-Paristech, CNRS, Ecole Polytechnique, Institut Polytechnique de Paris, Palaiseau.