D. S. Inosov1, J. T. Park1, P. Bourges2, D. L. Sun1, Y. Sidis2, A. Schneidewind3,4, K. Hradil4,5, D.Haug1, C. T. Lin1, B. Keimer1, and V. Hinkov
1 Max-Planck-Institut für Festkörperforschung, Heisenbergstraße 1, 70569 Stuttgart, Germany
2 Laboratoire Léon Brillouin, CEA-CNRS, CEA Saclay, 91191 Gif-sur-Yvette, France
3 Forschungsneutronenquelle Heinz Maier-Leibnitz (FRM-II), TU München, D-85747 Garching, Germany
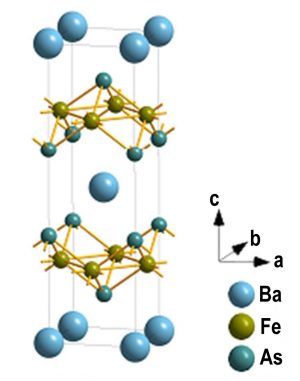
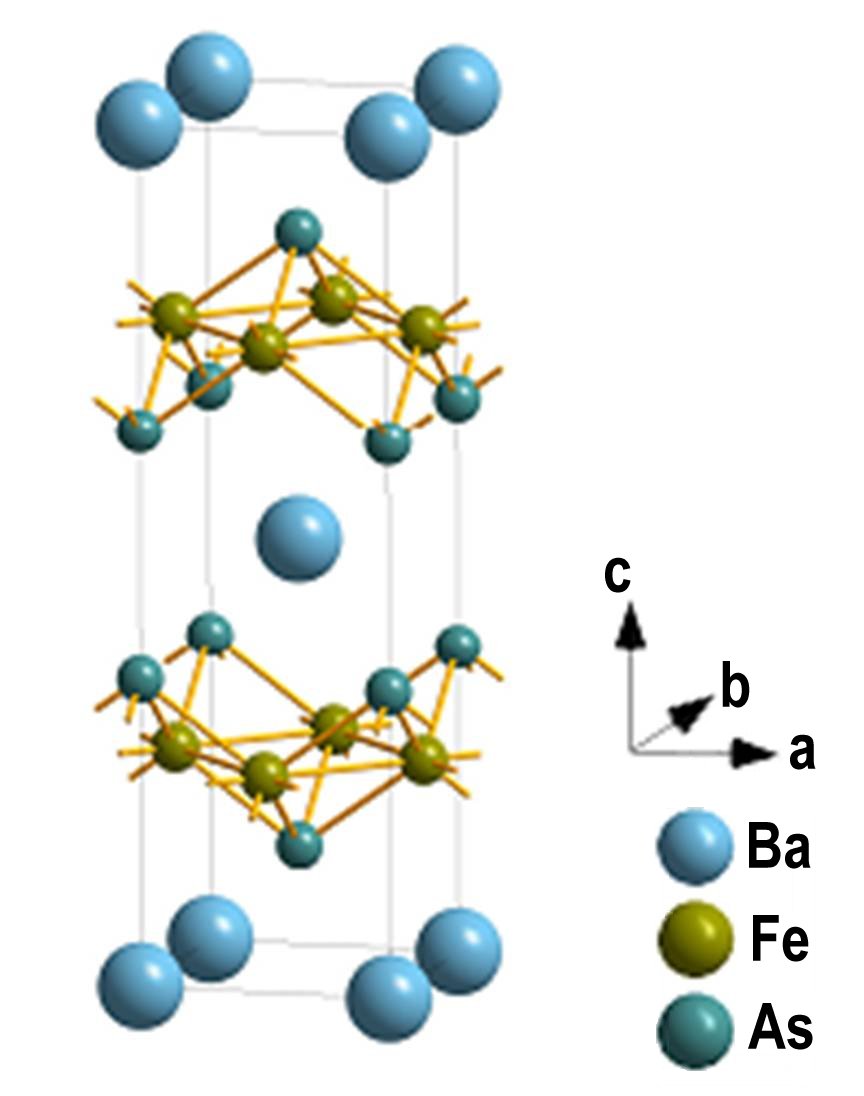
In March 2008, superconductivity at high critical temperature (Tc> 50K) was found in iron-arsenide compounds [1] to the surprise of the scientific community. Indeed, the magnetic iron was rather regarded as an antagonist of superconductivity. Moreover, it is the first time that a so high critical temperature is reached without copper. Very like copper oxide superconductors, these new superconductors have a lamellar structure with layers of iron and “pnictures” (compounds of As, P. .., that are elements of the 15th column of the Mendeleyev table) which are interposed between plans of “charge reservoirs” (see figure). These materials also present a phase diagram similar to that of cuprates with, versus the doping concentration, an antiferromagnetic phase adjacent to the superconducting zone ( [2]).
Superconductivity is related to the pairing of conduction electrons in “Cooper” pairs. For heavy fermion systems * as well for high critical temperature copper oxide superconductors, it was widely suggested that superconductivity could be related to a mechanism with a magnetic origin. However, the existence of strong electronic correlations and competing phases complicates the situation and makes difficult the validation of a magnetic model for superconductivity. In Fe-arsenide compounds, the proximity of the superconductive and antiferromagnetic phases in the phase diagram strongly renews the hypothesis of Cooper pairs stabilized by magnetic fluctuations. This option is more plausible as the electron-phonon coupling responsible for the usual superconductivity, is significantly low in these materials.
To establish the validity of this assumption, the detailed spectrum of magnetic excitations above the superconducting transition Tc must be known. Indeed, most theories of superconductivity implies the existence of an attractive interaction between electrons already present in the normal state (T > Tc). Moreover this “glue” must be strong enough to lead to superconductivity state at high critical temperature (Tc).
Atomic structure of the BaFe2As2 compound that presents an antiferromagnetic order. The substitution of Fe by Co allows an electronic doping. With a 15% Co doping, the magnetic transition temperature is lowered and the superconductivity appears below a critical temperature of 25 K.
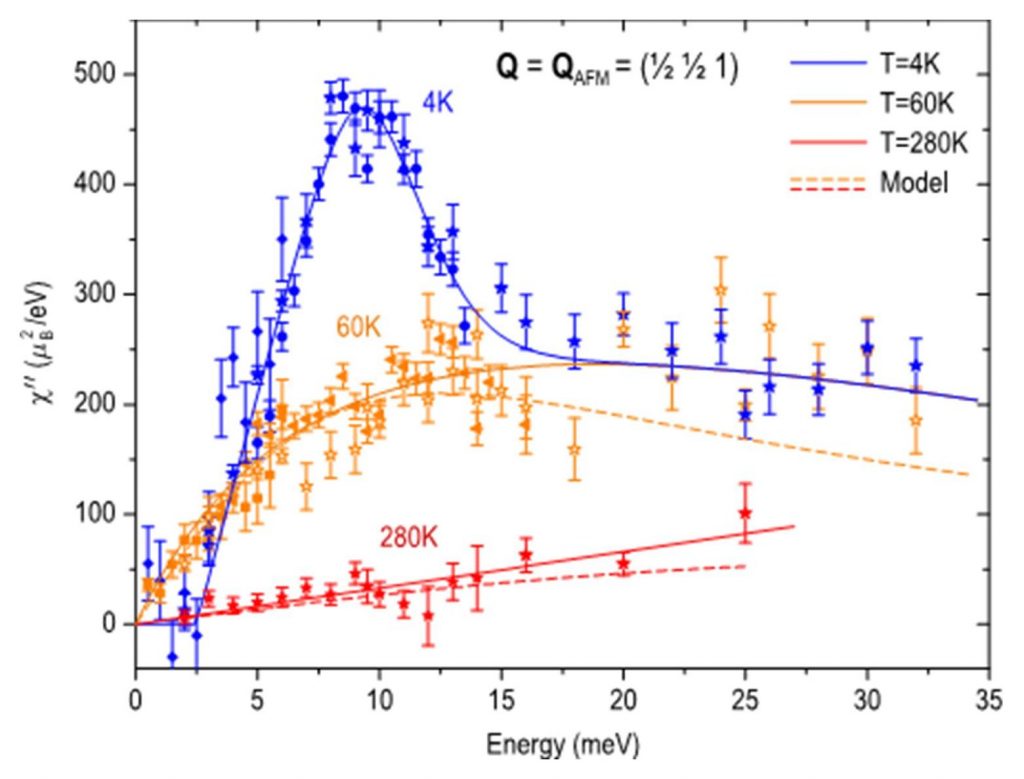
By inelastic neutron diffusion** the magnetic susceptibility of the optimally doped BaFe1.85Co0.15As2 compound (Tc = 25 K) has been measured over a wide range of energy and temperature [3]. The cross section for neutron scattering is directly proportional to the imaginary part of the magnetic susceptibility χ′′ (that is in turn related to the attenuation due to losses in the solid). The χ′′ absolute value is shown in the figure for the normal and superconducting phases. In the normal state, the spectral weight of magnetic fluctuations is consistent with the predictions of the theory for a metal with antiferromagnetic correlations (see the model describing the data in the figure). This itinerant magnetism is induced by specific topological properties of the Fermi surfaces. In the superconducting phase, a resonance peak around 9.5 meV can be observed with the opening of a spin gap of 3 meV. With the temperature, the energy of this resonance decreases very like the thermal evolution of twice the superconducting gap (that is the energy required to break a Cooper pair) as predicted by the conventional theory of itinerant magnetism.
All these observations imply that the dynamics of spins in Fe-arsenide compounds can be simply described by a theory of itinerant magnetism that is expected for a Fermi liquid. This creates a strong basis for models where the superconductivity is magnetically induced.
* Heavy fermion system: metals with strong interactions between f-type electrons and electrons from the conduction band. The effective mass of electrons is typically 100-1000 times that of a free electron!
** Work done within the “Orphée” high flux neutron reactor at the Léon Brillouin Laboratory (CEA – CNRS, Saclay) and within the reactor FRMII-Garching (Germany).
References :
[1] Superconductivity at 43 K in SmFeAsO1-xFx
X. H. Chen, T. Wu, G. Wu, R. H. Liu, H. Chen & D. F. Fang, Nature 453, 761-762 (2008).
[2] Hall Effect and Resistivity Study of the Magnetic Transition, Carrier Content, and Fermi-Liquid Behavior
in Ba(Fe1-xCox)2As2
F. Rullier-Albenque, D. Colson, A. Forget, and H. Alloul, Phys. Rev. Letters 103, 057001 (2009).
| [3] Normal-state spin dynamics and temperature-dependent spin resonance in an optimally electron-doped iron arsenide superconductor, D. S. Inosov, J. T. Park, P. Bourges, D. L. Sun, Y. Sidis, A. Schneidewind, K. Hradil, D.Haug, C. T. Lin, B. Keimer and V. Hinkov, Nature Phys. 6 (2010) 178. |
|
Press release of the Max-Planck-Institut für Festkörperforschung of Stuttgart (in german).